 |
Итерационные методы решения СЛАУ
|
|
|
|
Найти решение СЛАУ с матрицей 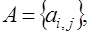
 и правой частью
и правой частью  итерационными методами Якоби, Зейделя и ОСП. Решение получить с заданной относительной точностью
итерационными методами Якоби, Зейделя и ОСП. Решение получить с заданной относительной точностью  . Указать количество итераций
. Указать количество итераций 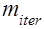 необходимых каждому методу для достижения заданной точности. В случаях слабой сходимости ограничиться числом
необходимых каждому методу для достижения заданной точности. В случаях слабой сходимости ограничиться числом  , отразив это в результатах. Отметить также случаи явной расходимости метода.
, отразив это в результатах. Отметить также случаи явной расходимости метода.
В качестве оптимального параметра 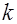 для сходимости метод ОСП в задаче с матрицей размером
для сходимости метод ОСП в задаче с матрицей размером 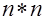 следует принимать:
следует принимать:
· 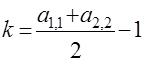 , в случае
, в случае 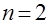 (и в случае периодического продолжения на трехдиагональную матрицу с большими значением
(и в случае периодического продолжения на трехдиагональную матрицу с большими значением 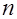 )
)
·  , для задач с трехдиагональной матрицей с постоянной главной диагональю, где
, для задач с трехдиагональной матрицей с постоянной главной диагональю, где 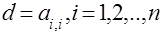 . В частности, для матриц с
. В частности, для матриц с  .
.
В случаях расходимости всех трех используемых методов следует применить комбинированный метод Якоби-Зейделя и ОСП. Для этого потребуется найти собственные числа матрицы Якоби [5.3.2.3] и на этой основе сделать вывод о значении 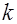 для ряда оптимальной простой итерации с матрицей [5.3.3.1], в которой
для ряда оптимальной простой итерации с матрицей [5.3.3.1], в которой  -матрица Якоби. Этот же оптимальный параметр можно использовать для построения ряда простой итерации с оператором [5.3.3.1], где
-матрица Якоби. Этот же оптимальный параметр можно использовать для построения ряда простой итерации с оператором [5.3.3.1], где  -оператор Зейделя [5.3.2.5]. Однако, в последнем случае оптимальный параметр, как правило, может быть значительно улучшен и в необходимых случаях он указан.
-оператор Зейделя [5.3.2.5]. Однако, в последнем случае оптимальный параметр, как правило, может быть значительно улучшен и в необходимых случаях он указан.
Варианты заданий.
| № вар. | 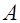
| 
| 
| Примечание |
| 1. | 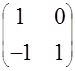
| 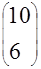
| 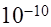
| |
| 2. | 
| 
| 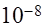
| |
| 3. | 
| 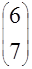
| 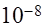
| Оптимальный параметр для метода Зейделя-ОСП k=0.1 |
| 4. | 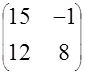
| 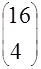
| 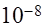
| |
| 5. | 
| 
| 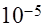
| |
6. 
| 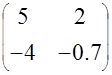
| 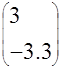
| 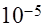
| |
| 7. | 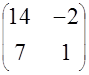
| 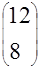
| 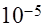
| Оптимальный параметр для метода Зейделя-ОСП k=0.25 |
| 8. | 
| 
| 
| Оптимальный параметр для метода Зейделя-ОСП k=2 |
| 9. | 
| 
| 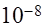
| Оптимальный параметр для метода Зейделя-ОСП k=1 |
| 10. | 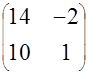
| 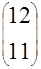
| 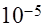
| Оптимальный параметр для метода Зейделя-ОСП k=1 |
| 11. | 
| 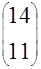
| 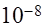
| |
| 12. | 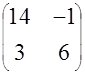
| 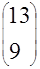
| 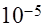
| |
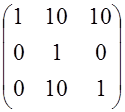
| 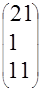
| 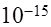
| ||
14. 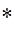
| 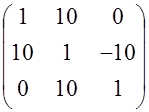
| 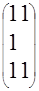
| 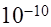
| |
15 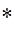
| 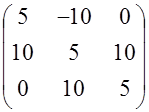
| 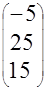
| 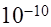
|
|
|
|
При выполнении лабораторных работ с помощью пакета Mathcad указанные варианты видоизменяются до больших трехдиагональных матриц с  . Для этого главная и две побочные диагонали периодически продолжаются на большую матрицу. Остальные коэффициенты матрицы нулевые. Так, матрица варианта №2 выглядит следующим образом:
. Для этого главная и две побочные диагонали периодически продолжаются на большую матрицу. Остальные коэффициенты матрицы нулевые. Так, матрица варианта №2 выглядит следующим образом:
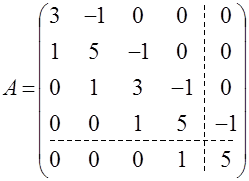
Оптимальный параметр 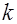 для метода ОСП остаётся при этом неизменным (несмотря на трансформацию спектра матрицы- увеличение радиуса круга
для метода ОСП остаётся при этом неизменным (несмотря на трансформацию спектра матрицы- увеличение радиуса круга 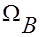 при неизменном положении его центра) и определяется так, как указано выше для малых матриц.
при неизменном положении его центра) и определяется так, как указано выше для малых матриц.
В качестве вектора правой части взять вектор с  для всех
для всех  . Относительная точность вычислений для всех вариантов
. Относительная точность вычислений для всех вариантов 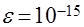 .
.
Варианты помеченные * используются только для практических работ с n=2 и для n=100 решений в виде сходящегося итерационного процесса не имеют. В этом случае выбирается вариант с номером = 16 - №вар.
В результате работы представить для каждого метода:
· вектор решения (несколько первых компонент)
· число итераций
· невязку решения
· спектр оператора (с помощью стандартных функций Mathcad)
· сравнить значение оптимального параметра, полученного исходя из знания спектра оператора, и использованного Вами в решении.
Сравнить решение СЛАУ, полученное стандартным методом Mathcad и Вашим итерационным методом.
Сделать вывод о причинах хорошей (плохой) сходимости итерационного метода.
Найти число обусловленности исходной матрицы (с помощью стандартных функций Mathcad).Для вариантов задания с быстрой сходимостью ( ) сравнить при
) сравнить при  время решения СЛАУ стандартным методом Mathcad и итерационным методом.
время решения СЛАУ стандартным методом Mathcad и итерационным методом.
Нахождение собственных значений и векторов
Пример: Найти собственные вектора и значения матрицы:
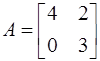
Выберем 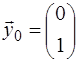 , тогда:
, тогда:
 ,
,  .
.
СЛАУ имеет вид:
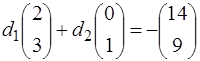 , откуда
, откуда 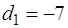 ,
, 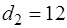 в результате получаем характеристический полином:
в результате получаем характеристический полином:
|
|
|
 , откуда
, откуда  ,
,  .
.
Построим полиномы для нахождения собственных векторов:
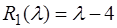 ,
, 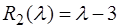 ,
,
Поэтому:
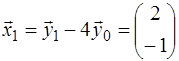 ,
, 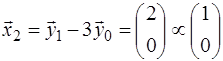 , так как собственный вектор определен с точностью до произвольного множителя.
, так как собственный вектор определен с точностью до произвольного множителя.
Проверка:
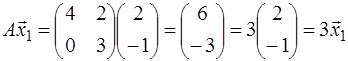 ,
,
 .
.
|
|
|


