 |
Интерполяционные полиномы.
|
|
|
|
Полином степени n однозначно определяется своими значениями в n+1 точке с попарно разными абсциссами: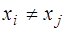 
, если 
. Действительно, выпишем согласно критерию интерполяции систему уравнений 
или в развернутом виде:
.
Система (n+1)-ого уравнения относительно 
, 
имеет единственное решение, если 
так как в этом случае её определитель не равен 0.
Существуют методы, позволяющие избежать непосредственного решения системы уравнений для нахождения .
2.2 Интерполяционный полином Лагранжа
Рассмотрим в начале n=1:
.
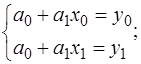
Подставляя коэффициенты в 
, получим:
то есть полином представлен в виде суммы двух линейных функций, независящих от ординат, умноженных на ординаты и обладающих свойством:
.
В этом состоит идея построения интерполяционного полинома Лагранжа. Для произвольного значения n запишем интерполяционный полином в виде:
,
где 
полиномы степени не выше n, не зависящие от ординат, и обладающие следующими свойством: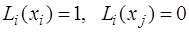 
.
Из равенства, 
следует, что имеет n корней (рассматриваются однократные корни).
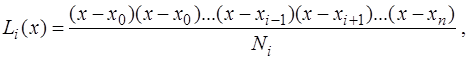
где 
- коэффициент, который находится из условия 
.
В результате интерполяционный полином Лагранжа имеет вид:
(2.1)
Достоинства интерполяционного полинома Лагранжа является простота конструкции. При заданном наборе абсцисс узловых точек и выбранной расчетной точке 
упрощается вычисления для различных ординат 
. Недостаток – добавление (n+1)-ого узла 
требует перерасчета всех слагаемых.
Погрешность вычисления: пусть 
– функция n + 1 – раз дифференцируемая и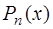 
– приближающий её интерполяционный полином.
,
где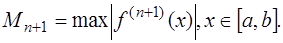 
Интерполяционный полином Лагранжа при линейных преобразованиях x = at + b (t- новая переменная) – сохраняет свой вид.
Интерполяционный полином Ньютона.
|
|
|
Пусть n =0, тогда 
, если
n =1, то выражение для полинома можно записать в виде: 
, т. е. поведение приближающей функции с добавлением узлов, уточняется вблизи точки х0. Конструкция интерполяционного полинома Ньютона такова:
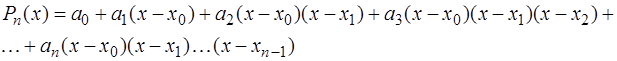
Рассматривается равномерная сетка, т.е. 
.
Для дальнейшего анализа вводится понятие конечной разности. Конечной разностью первого порядка называется величина
.
Конечная разность второго порядка определяется по первой
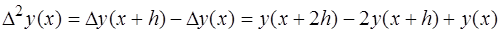
и т.д. конечная разность i – ого порядка определяется через рекуррентное соотношение:
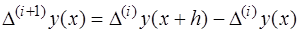
и зависят от значений y в (i + 1) – ой точке.
Выражение вида: 
называется обобщенным произведением. Его первая конечная разность равна:
. (2.2)
Отсюда следует выражение для конечных разностей высших порядков.
Подставляя 
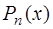в , получим: 
. Далее, определим конечную разность в точке 
. Из свойства (2.2) получим:
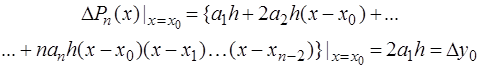
Отсюда следует, что 
. Точно также из (2.2) следует выражение для конечной разности второго порядка в точке :
.
Общая формула имеет вид: 
.
В результате получаем первый интерполяционный полином Ньютона:
(2.3)
Построенный таким образом интерполяционный полином проходит через узловые точки.
Второй интерполяционный полином Ньютона позволяет начать интерполяцию с точки 
, т.е. улучшить точность приближения на правой границе интервала интерполяции
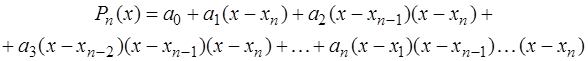
Из структуры полинома следует, что 
.
;
; 
; и так далее. Окончательно получим:
; (2.3)
При расчётах и алгоритмизации вычисления интерполяционного полинома применяется таблица конечных разностей:
Таблица 2.2
| № | 
| 
| 
| 
| 
| … |
|
| 
| 
| 
| 
| … | |
| 
| 
| 
| … | ||
| 
| 
| … | |||
| 
| … | ||||
| … | … | … |
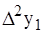
Для построения 1-ого интерполяционного полинома Ньютона необходима 1-ая строка табл. 2.2. Для построения 2-ого интерполяционного полинома Ньютона необходима побочная диагональ таблицы. Обычно при машинных расчётах массив ординат узловых точек последовательно преобразуется в массив коэффициентов 
, так что они запоминаются в соответствующих элементах массива.
|
|
|
|
|
|
