 |
Задание к теме и пример решения ОДУ
|
|
|
|
Найти решение задачи Коши для ОДУ:
, 
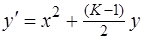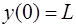на интервале 
. K и L параметры из табл.
Решить пятью методами:
1. Метод вариации постоянных (точное решение).
2. Разложение в ряд Тейлора до четвертого порядка.
3. Метод Эйлера (6.3.1.1).
4. Метод трапеций (Коши-Эйлера) (6.3.2.1).
5. Метод Рунге-Кутта (6.4.1).
Построить графики и сравнить точность различных методов, шаг 
.
1. В методе вариации постоянных решение ищется в виде 
, Однородное уравнение 
имеет очевидное решение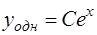 
. Подстановка в неоднородное уравнение дает уравнение для коэффициента: 
. После интегрирования и подстановки начального условия получим: 
.
2. Разложение в ряд Тейлора проводится в точке х =0. Все производные в этой точке известны 
;
, 
;
, 
;
, 
.
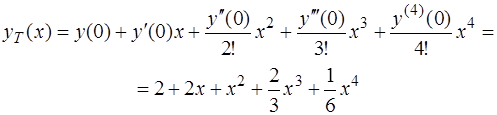
3. Метод Эйлера. Расчет ведется по формуле (6.3.1.1):
4. Метод Коши-Эйлера (метод трапеций). Вначале рассчитывается значение 
, которое затем используется в окончательном выражении (6.3.2.1).
6. Метод Рунге-Кутта. Последовательно вычисляются значения производной в промежуточных точках и используются в окончательном выражении с заданными весами (6.4.1).
Пример. К =3, L= 2. 
, 
.
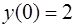Результаты расчетов представлены в таблице:
| x | 0,5 | 1,5 | |||
| Точное решение | 3,34488 | 5,87313 | 10,6768 | 19,5562 | |
| Ряд Тейлора | 3,3438 | 5,83333 | 10,3438 | ||
| Метод Эйлера | 4,625 | 7,4375 | 12,2812 | ||
| Метод Коши- Эйлера | 3,3125 | 5,72656 | 10,2432 | 18,4889 | |
| Метод Рунге- Кутта | 3,34440 | 5,87111 | 10,6710 | 19,5423 |
Литература
1. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970. – 644с.
2. Бахвалов Н.С., Жидков Н.П., Кобельников Г.М. Численные методы. – М.: Наука, 1987. – 598с.
3. Калиткин Н.Н., Численные методы. – М.:Наука, 1978.– 512с.
4. Заварыкин В.М., Житомирский В.Г., Лапчин М.П. Численные методы. – М.: Просвещение, 1991. – 176с.
|
|
|
Содержание.
Введение. 3
1. Абсолютная и относительная погрешности. 3
1..1 Число верных знаков приближенного числа. 4
1.2 Погрешность функций. 4
1.3 Погрешность простейших функций двух переменных. 5
1.4 Примеры и задания. 6
2. Приближение функций. 10
2.2 Интерполяционный полином Лагранжа. 11
2.3 Интерполяционный полином Ньютона. 12
2.3 Примеры и задания для практических занятий. 15
3. Численные методы решений трансцендентных и алгебраических уравнений. 18
3.1 Метод простой итерации для решения нелинейных и трансцендентных уравнений. 19
3.2 Метод хорд и секущих. 20
3.3 Метод касательных. 21
3.4 Скорость сходимости итерационных методов. 21
3.5 Пример и задание для практических занятий. 23
4. Численное интегрирование. 24
4.1 Метод Ньютона – Котеса. 25
4.2 Метод прямоугольников. 26
4.3 Метод трапеций. 27
4.4 Оценка погрешности метода. 27
4.5 Метод парабол. (Метод Симпсона) 28
4.6 Оценка погрешности метода парабол. 28
4.7 Квадратурные формулы Гаусса. 29
4.8 Задание для практических занятий. 31
5. Численные методы линейной алгебры. 32
5.1. Численное решение СЛАУ. 32
5.2 Прямые методы решения СЛАУ.. 35
5.2.1 Метод Гаусса (Метод исключений) 35
5.2.2 Вычислительная схема метода Гаусса. 36
5.2.3 Ортогонализация матриц. 39
5.2.4 Решение системы уравнений методом ортогонализации. 40
5.3. Итерационные методы решения СЛАУ. 41
5.3.1. Метод простой итерации. 41
5.3.2. Метод Якоби и метод Зейделя. 43
5.3.3. Метод оптимального спектрального параметра (ОСП) для простой итерации. 45
5.4. Нахождение собственных векторов и собственных значений матриц. 48
5.5. Примеры и задания к теме. 50
5.5.1. Точные методы решения СЛАУ.. 50
5.5.2. Итерационные методы решения СЛАУ.. 53
5.5.3 Нахождение собственных значений и векторов. 57
6. Численные методы решения обыкновенных дифференциальных уравнений. 58
6.1 Метод разложения в ряд Тейлора. 59
6.2. Общая схема метода Рунге - Кутта. 59
|
|
|
6.3 Методы Рунге-Кутта низших порядков. 60
6.3.1 Метод Эйлера. 60
6.3.2. Метод трапеций и прямоугольника. 61
6.4. Методы Рунге-Кутта высших порядков. 61
6.5. Задание к теме и пример решения ОДУ.. 63
Литература. 64
Содержание. 65
|
|
|
