 |
Задание для практических занятий.
|
|
|
|
Дана матрица  Найти ее собственные значения и вектора.
Найти ее собственные значения и вектора.
Варианты:
1)  , 2)
, 2) 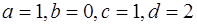 ,
,
3)  , 4)
, 4)  ,
,
5) 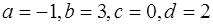 , 6)
, 6)  ,
,
7)  , 8)
, 8)  ,
,
9)  , 10)
, 10)  ,
,
11)  , 12)
, 12)  ,
,
13)  , 14)
, 14) 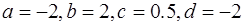 ,
,
15)  , 16)
, 16)  .
.
Численные методы решения обыкновенных дифференциальных уравнений
Рассматриваются уравнения первого порядка, разрешимые относительно первой производной с начальными условиями  :
:
 (6.1)
(6.1)
Существует теорема Коши о единственности решения дифференциального уравнения при заданных начальных условиях  . Геометрически
. Геометрически  определяет поле направлений на плоскости
определяет поле направлений на плоскости  , а решения обыкновенного дифференциального уравнения (ОДУ) - интегральные кривые.
, а решения обыкновенного дифференциального уравнения (ОДУ) - интегральные кривые.
Численные методы решения задачи Коши для ОДУ основаны на том, что решение можно представить в виде разложения в ряд Тейлора с любой степенью точности.
Метод разложения в ряд Тейлора.
Решение ищется в виде

Функциональные зависимости  известны:
известны:
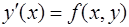 ,
,
 , (6.2)
, (6.2)
 и т.д.
и т.д.
Этот метод приводит к громоздким выражениям для производных, и в основном используются для получения других численных методов.
Общая схема метода Рунге - Кутта
Одношаговые методы позволяют получить заданную точность используя только предыдущее значение  . Изменение
. Изменение  на шаге h представляется в виде квадратурной формулы (типа Гаусса):
на шаге h представляется в виде квадратурной формулы (типа Гаусса):
 ,
,
где  .
.
Для получения коэффициентов  ,
,  и
и  квадратурная сумма разлагается в ряд по степеням h. Полученное разложение сравнивается с рядом Тейлора:
квадратурная сумма разлагается в ряд по степеням h. Полученное разложение сравнивается с рядом Тейлора:
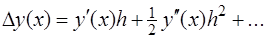 (6.2.1)
(6.2.1)
В общем виде выражения для коэффициентов получить трудно, поэтому рассмотрим наиболее употребительные формулы.
Введем обозначения:
 ,
,
 , (6.2.2)
, (6.2.2)
 ,
,
………………………………………….

Квадратурную формулу разлагаем в ряд по h:
 (6.2.3)
(6.2.3)
¦  , ¦
, ¦  , ¦
, ¦  , ¦
, ¦  -- частные производные по x и y ¦(x, y).
-- частные производные по x и y ¦(x, y).
|
|
|
Полученное разложение сравнивается с рядом Тейлора (6.2.1).
Рассмотрим несколько частных случаев.
Методы Рунге-Кутта низших порядков
Метод Эйлера
В квадратурной формуле ограничиваемся одним слагаемым:
 . (6.3.1.1)
. (6.3.1.1)
Интегральная кривая заменяется ломаной линией, состоящей из прямолинейных отрезков. Выбирается шаг h и значение функции в точке 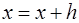 ищется по формуле
ищется по формуле 
т.е. в интегральном уравнении f(x,y) заменяется на константу.
Ошибки метода 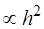 так как в ряде Тейлора отбрасываются вторые производные.
так как в ряде Тейлора отбрасываются вторые производные.
Метод трапеций и прямоугольника
Это популярные методы, иначе их называют метод Коши- Эйлера и модифицированный метод Эйлера, их ошибка 
Представление  - позволяет сравнить два первых слагаемых в разложении с рядом Тейлора:
- позволяет сравнить два первых слагаемых в разложении с рядом Тейлора:
 ,
, 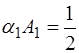 ,
, 
Получены три уравнения для четырех неизвестных, что является общим свойством метода Рунге- Кутта. То есть для каждого порядка точности существует множество вычислительных схем:  ,
,  .
.
Положим  , тогда
, тогда
 , (6.3.2.1)
, (6.3.2.1)
то есть значение производной «подправляется» значением в предварительно определенной точке.
 , тогда
, тогда  ,
, 
В этом случае 
Методы Рунге-Кутта высших порядков
В методе Рунге- Кутта третьего порядка точности:

Разлагая в ряд по h до h 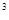 и сравнивая с рядом Тейлора (7.2.1)получим следующую систему из шести уравнений для восьми неизвестных:
и сравнивая с рядом Тейлора (7.2.1)получим следующую систему из шести уравнений для восьми неизвестных:

Наиболее употребительна в этом случае симметричная разностная схема (аналог метода парабол при численном интегрировании):  , тогда:
, тогда:
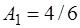 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
 ,
,
 ,
,
 ,
,
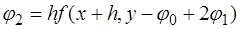 .
.
В методе Рунге-Кутта точности порядка  получается система из 11 уравнений для 13 неизвестных.
получается система из 11 уравнений для 13 неизвестных.
Наиболее употребительны две вычислительные схемы:
1. Аналог метода 3/8 в численном интегрировании.
 , где
, где
 ,
,
 ,
,
 ,
,
 ,
,
2. Аналог метода парабол.
 , (6.4.1)
, (6.4.1)
где  ,
,
 ,
,
 ,
,
 .
.
Проблема выбора той или иной вычислительной схемы при заданной точности зависит от вида ¦(х,у), так как от этого зависит величина остаточного члена.
|
|
|
|
|
|


