 |
Скорость сходимости итерационных методов.
|
|
|
|
Для оценки скорости сходимости необходимо найти связь между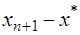 
и 
.
В случае метода простых итераций:
,
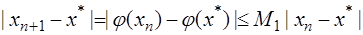то есть скорость сходимости линейная.
Несмотря на схожесть выражений для метода хорд и секущих скорость их сходимости различна, так для метода хорд получим разлагая выражение для 
в точке 
в ряд Тейлора и ограничиваясь тремя слагаемыми:
Учитывая, что 
, сокращая в числителе и знаменателе 
и разлагая знаменатель в ряд, получим:
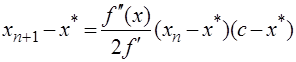(3.8)
Оценка (3.8) с учетом того, что расстояние между точками и 
меньше длины интервала изоляции дает:
, (3.9)
то есть скорость сходимости линейная.
В методе секущих в выражении (3.9) необходимо заменить на 
. Предположим, что соотношение для скорости сходимости имеет вид:
.
Подставляя полученное из него выражение для 
в (3.8) получим для степеней r и t:
, и 
, 
, 
.
Сходимость такого вида называется сверхлинейной.
Для метода касательных, вычитая из левой и правой части (3.6) значение корня и разлагая функцию в ряд, получим:
Откуда:
, (3.10)
То есть сходимость метода касательных квадратичная.
Метод хорд используется в тех случаях, когда анализ поведения второй производной затруднен. Если точки перегиба на интервале изоляции нет, то используется метод секущих или, если вычисление второй производной не требует значительного машинного времени, то быстрее всего сходящийся метод касательных.
Пример и задание для практических занятий.
Пример. Найти методом хорд, касательных и простой итерации корни уравнения:
, К =20, L =10. (3.12)
Каждый корень искать одним из предложенных методов. Для этого вначале необходимо отделить корни и выбрать метод решения. Рекомендуемый план решения приводится ниже:
|
|
|
1) Находятся первая и вторая производные:
, 
.
Очевидно, что корни (если они существуют) расположены левее, между и правее точек экстремума функции
.
Выбираются три интервала [ a, b ] и проверяется условие (3.1) на каждом интервале.
2) Для метода простых итераций уравнение преобразуется к итерационному виду: 
и выбирается интервал [a ,b ]= [3 ,5 ], на котором проверяется выполнение условия (3.1). В качестве начального значения выбирается 
, тогда 
, 
.
3) Для метода хорд выбирается интервал [a ,b ]= [-3, 3] и проверяется (3.1) 
, неподвижной точки на этом интервале не существует, поэтому каждый раз находится новый интервал из условия (3.1), в результате, применяя (3.3) получим два последовательных приближенных значения корня: 
, 
.
4) Для метода касательных выбирается интервал [a ,b ]= [-3 ,- 5] и проверяется выполнение условия (3.1) 
, выбирается начальная точка из условия (3.3): 
. По формуле (3.7) проводятся две итерации: 
, 
.
Варианты для практических занятий приведены в табл.4.1:
Таблица 4.1
| № | ||||||||||||||||
| К | ||||||||||||||||
| L |
Численное интегрирование
Цель – приближенно вычислить определенный интеграл: 
на [ a,b ].
По теореме Ньютона – Лейбница он равен разности верхнего и нижнего пределов первообразной 
(
) функции. Но для табличных функций их первообразная не существует и даже для известных 
не всегда представима в виде комбинаций элементарных функций. Интеграл геометрически равен площади криволинейной трапеции.
В численных методах интеграл ищется в виде квадратуры: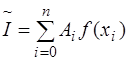 
. Необходимо найти оптимальным образом 
и 
. Обычно коэффициенты подбираются так, чтобы квадратура давала точное значение для полинома максимально возможной степени.
|
|
|
Метод Ньютона – Котеса
Предполагается, что значения аргументов известны и расположены равномерно. Требуется найти коэффициенты А.
Рассмотрим интервал: 
, 
.
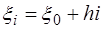На интервале заменим интерполяционным полиномом Лагранжа (2.1), подставляя в него переменную q, равную:
.
, получим 
,
где штрих означает отсутствие в произведении сомножителя с j=i
коэффициенты Аi равны:
, (4.1)
где 
не зависящие от интервала [ a,b ] – коэффициенты Котеса.
В дальнейшем рассматривается равномерная сетка узлов с шагом h.
Метод прямоугольников.
Степень полинома n = 0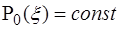 
. Коэффициент Котеса (4.1) при n = 0 (вычисляется как предельный переход при 
) равен 1.Интервал 
неопределен, т.к. есть только одна точка -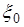 
. Геометрически это обозначает, что f(x) заменяется на интервале каким-то значением ординаты. Если интервал [ a,b ] велик, то его разбивают точками на n интервалов и на каждом применяют метод прямоугольников. Для первого интервала приближенное значение интеграла равно 
, где 
.
В качестве 
обычно применяют:
- метод левых прямоугольников;
- метод правых прямоугольников.
На [ 
] повторяют ту же процедуру и результат суммируют
, 
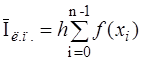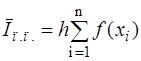. (4.2)
Погрешность метода на интервале длиной h равна: 
дифференцируя по h, получим: 
, 
. После интегрирования по h: 
. Абсолютная погрешность на n интервалах суммируется. В результате, учитывая, что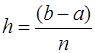 
получим: 
, где 
.
Метод трапеций.
На частичном интервале функция заменяется линейной, т.е. n= 1. 
, 
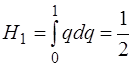. На интервале 
, заменяя f(x) на P1(x), получим для равноотстоящих узлов: 
. То есть, площадь криволинейной трапеции заменена площадью прямоугольной трапеции.
Суммируя по всем интервалам, приходим к выражению: 
, в котором внутренние ординаты встречается дважды. Окончательно получим: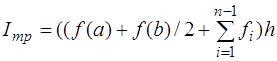 
. (4.3)
Между методом трапеций и методом прямоугольников существует простая связь:
(4.4)
Оценка погрешности метода
Продифференцируем соотношение дважды по 
:
,
, 
.
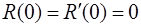Интегрируя 
дважды с заменой 
на среднее значение, приходим к выражению:
.
Погрешность на интервале интегрирования есть сумма погрешности на каждом частичном интервале, мажорируя вторую производную, получим: 
.
|
|
|
