Обоснование и распределение требований к надежности элементов

ЭЛЕКТРИЧЕСКИХ АППАРАТОВ

При решении задачи об обосновании количественных требова­ний к надежности ЭА приходится учитывать множество самых разнообразных и, как правило, противоречивых факторов. Среди них на первом месте стоят вопросы эффективности, на втором — экономические показатели, на третьем — реальные условия экс­плуатации и т. д. Кроме этого необходимо принимать во внима­ние технологические возможности промышленности. В общем слу­чае обоснование требований к надежности сложных технологиче­ских объектов связано с соизмерением затрат в производстве и эксплуатации, вызванных изменением надежности оборудования. Обоснование требований к надежности ЭА — задача оптимизаци­онная. В общей постановке решение предполагает нахождение минимума функционала

(8.2)

где C_i(P _i)— приведенные затраты на элементы ЭА, зависящие от уровня его надежности; C_РE3(P_i,П_э) — затраты на создание резер­ва мощности в энергосистеме, которые зависят как от характери­стик надежности основных элементов ЭА так и от рас­четного уровня надежности энергоснабжения потребителей П_э; С_У(П_Э) — ущерб от недоотпуска энергии; С_ЭК (Р_i) — затраты на ли­квидацию возможных последствий ненадежности оборудования экологического характера.

Решение оптимизационной задачи (8.2) из-за существенной неопределенности исходной информации в настоящее время чрез­вычайно сложно. Рассмотрим один из возможных путей. Из опы­та известно, что затраты (стоимость) на разработку и производст­во сложных ЭА увеличиваются по мере возрастания их надежно­сти. При изменении ВБР в пределах 0,2...0,8 увеличение стоимости идет плавно, а в пределах 0,8... 1,0 — резко, приближаясь к бесконечности при P (t)=1,0 (кривая 1на рис. 8.2). Эта кривая может быть аппроксимирована зависимостью вида

(8.3)

где — постоянная величина стоимости, не зависящая от на­дежности; — стоимость разработки и производства системы, обладающей ВБР Р _о.

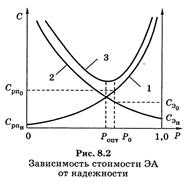где Срп_н — постоянная величина стоимости, не зависящая от на­дежности; С_РПо — стоимость разработки и производства системы, обладающей ВБР Р_о.

ЭА, имеющий низкую надеж­ность, как правило, имеет высо­кую стоимость при эксплуата­ции. Это объясняется большими затратами на проведение плано­вых профилактических ремон­тов (ППР), осмотров, проверок, отыскание и устранение отказов. Все это требует содержания обслуживающего персонала с отно­сительно высокой квалификаци­ей, наличия контрольно-измери­тельной аппаратуры и т. п. По мере увеличения надежности затраты на эксплуатацию ЭА умень­шаются. Типичная зависимость стоимости эксплуатации ЭА от на­дежности (кривая 2 на рис. 8.2) может быть аппроксимирована выражением

(8.4)

где С_Эн — постоянная величина, не зависящая от надежности; С_Эо — стоимость эксплуатации ЭА, обладающей ВБР в течение Т лет. Общая стоимость всех затрат на разработку, производство и эксплуатацию ЭА:

(8.5)

Кривая зависимости суммарной стоимости ЭА от надежности приведена на рис. 8.2 (кривая 3). Из рисунка видно, что суммар­ная стоимость ЭА имеет минимум при определенном значении ВБР, которую назовем оптимальной величиной надежности по стоимости Р_ОПТ. Для вычисления Р_ОПТ необходимо взять производ­ную от выражения (8.5) и решить уравнение

В окончательном виде

(8.6)

Распределение требований к надежности составляющих ЭА элементов также предполагает решение оптимизационной зада­чи. В простейшем случае, когда отказы N элементов ЭА независи­мы и элементы равнонадежны,

Для нахождения связи надежности ЭА, надежности элемен­тов и стоимости ЭА и элементов воспользуемся следующей мето­дикой. Пусть для всех i -х элементов ЭА (i = 1,..., N) зависимость между надежностью и стоимостью разработки и изготовления определяется функцией вида

а между надежностью и стоимостью эксплуатации –

 

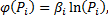
где α, и β — постоянные величины.

Стоимость ЭА складывается из затрат на составляющие его эле­менты, т. е.

(8.7)

Чтобы формула (8.7) выражала зависимость между надежно­стью и суммарной стоимостью, необходимо P_i (t)выразить через P (t). По определенному текущему значению надежности ЭА могут удовлетворять множества комбинаций значений P_i (t), дающих в произведении одно и то же значение P (t). Нас же интересует толь­ко такая комбинация произведений P_i (t), которая для данного зна­чения приводит к C_Σ =>min. Иначе, задача сводится к нахожде­нию таких значений Р _i (t), при которых ВБР ЭА равна Р(t), а стои­мость минимальна, т. е.

(8.8)

На основании метода Лагранжа минимизация стоимости ЭА может быть достигнута решением следующей системы уравнений:

(8.9)

где ω — неопределенный множитель.

После дифференцирования второго уравнения системы (8.9) получим

(8.10)

Обозначим ω Р = v, тогда после преобразований из выражения (8.10) имеем

(8.11)

Подставляя (8.11) в первое выражение системы (8.9), получаем

(8.12)

Из уравнения (8.9) и (8.12) следует, что между P (t)и P_i (t)име­ется сложная зависимость, затрудняющая непосредственное вы­ражение P_i (T)через P (t). Поэтому задачу можно решать методом имитационного моделирования. Задавая различные значения па­раметру v, находим текущие значения P (t)и соответствующие ком­бинации P_i(T), входящие в произведение P (t),при которых сум­марная стоимость ЭА будет минимальной для каждого значения P (t). По полученным значениям C_Σ и P (t)строится зависимость C_Σ = f(Р), из которой находится Р_опт.

 

8.4.

⇐ Предыдущая30313233343536373839Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: