Методы моделирования надежности сложных электрических аппаратов

Существуют сложные ЭА, работу которых не удается описать математически, задав систему уравнений, позволяющую найти количественные закономерности между входными и выходными параметрами ЭА с учетом особенностей его функционирования. При физическом моделировании нередко натурное воспроизведе­ние процесса сопряжено с большими материальными затратами. В таких случаях единственным способом исследования является моделирование процесса функционирования ЭА на компьютере. Сложность физических процессов, включающих электромагнит­ные, тепловые и газодинамические, затрудняет создание модели функционирования аппарата. При этом функционирование ЭА рас­членяется на ряд элементарных процессов, каждый из которых формализируется (описывается аналитически, задается логиче­скими условиями и т. д.), а затем в заданной последовательности воспроизводится на компьютере.

Наибольшее распространение среди методов моделирования надежности систем получил метод статистического моделирова­ния (Монте-Карло).

Подготовка и моделирование надежности сложных ЭА на ком­пьютере осуществляется в следующей последовательности:

1) определение целевой направленности моделирования;

2) выбор показателей надежности и эффективности, которые либо определяются, либо оптимизируются при моделировании;

3) определение законов распределений случайных величин, используемых при моделировании, а также способов их воспроиз­ведения;

4) формализация моделируемых процессов, т. е. составление статистической модели в соответствии с целевой направленностью моделирования, выбранными показателями надежности и спосо­бом воспроизведения процесса функционирования;

5) разработка укрупненного моделирующего алгоритма, т. е. последовательности операций при моделировании в крупном пла­не, как правило, на языке словесного описания;

6) детальная разработка структуры алгоритма с использовани­ем алгоритмического языка;

7) реализация алгоритма на компьютере и анализ полученных результатов.

Рассмотрим некоторые из этих этапов, представляющие инте­рес для моделирования надежности сложных ЭА.

Так как задачи надежности вполне естественно аппроксими­руются случайными процессами, то их исследование статистиче­скими методами дает наибольший эффект. При этом наиболее час­то решаются следующие задачи.

Моделирование случайных событий. Случайные события (ис­правная работа, отказ, восстановление) появляются в процессе мо­делирования в соответствии с заданными вероятностями р₁, р₂,..., р_п. При статистическом моделировании используются случай­ные числа, равномерно распределенные в интервале [0,1].На прак­тике случайные числа вырабатываются либо самим компьютером по специальным алгоритмам (псевдослучайные числа), либо спе­циальной приставкой — датчиком случайных чисел. Предполо­жим, что в нашем распоряжении имеется последовательность слу­чайных чисел с функцией распределения F (x)в интервале [0, 1]. Для решения задачи отрезок [0, 1] разбивают на п отрезков таким образом, чтобы длина каждого i -гo отрезка равнялась вероятно­сти Р _i. Попадание случайного числа на определенный отрезок фик­сируется как факт свершения данного события. В компьютере этот процесс сводится к выбору случайного числа R_j и последователь­ной проверке условия

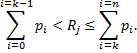
Длячастного случая, когда число возможных исходов п равно двум, например «исправен — неисправен», и вероятности этих событий Р (А)и 1 - Р (А), процесс воспроизведения события сво­дится к выбору случайного числа и однократной проверке усло­вия R_j < P (A). Если это условие выполнено, фиксируется выпол­нение события А. Эти же принципы используются и при модели­ровании зависимых случайных событий.

Получение случайных чисел с заданными законами распре­деления. Решение этой задачи основывается на известном в мате­матической статистике положении: если случайная величина х имеет плотность распределения f(x), то распределение случайной величины

является равномерным в интервале [0, 1]. Таким образом, сово­купность значений y_i = f (x_i)может интерпретироваться как после­довательность случайных величин, равномерно распределенных в интервале [0, 1]. Отсюда следует, что процесс получения после­довательности случайных чисел x_i с заданным законом распреде­ления F (x)сводится к решению относительно x_i уравнения

Формирование случайной величины по закону равной вероят­ности:

Формирование случайной величины по показательному закону:

Так как

То

 

 

Формирование случайной величины по закону Вейбулла:

Таким образом, получение случайных величин, распределен­ных по известному закону, сводится к формированию равномерно распределенных случайных чисел и преобразованию их по опре­деленной формуле.

Оценка точности результатов расчета и моделирования. В про­цессе моделирования и расчета надежности системы с помощью компьютера возможны ошибки. Оценки и основные факторы, их вызывающие, следующие:

■ ошибка определения входных величин (например, ошибки в определении интенсивностей и вероятностей отказов элемен­тов ЭА);

■ ошибка в представлении величин, вызванная ограниченностью числа разрядов компьютера;

■ ошибки операций;

■ ошибки расчетной формулы;

■ ошибки, вызванные сбоями в работе элементов компьютера;

■ ошибка, вызванная ограниченностью числа статистических реализаций.

В процессе моделирования вместо вероятностей используются частности, вместо математического ожидания — среднее значение случайной величины, вместо дисперсии — ее оценка и т. д.

Количество реализаций случайной величины N (количество опытов), точность ее воспроизведения (измеряется величиной до­верительного интервала, которым накрывается истинное значе­ние определяемого показателя), и достоверность того, что довери­тельный интервал накроет истинное значение определяемого по­казателя, взаимосвязаны.

Повышение точности, т. е. сужение доверительного интервала при сохранении доверительной вероятности, требует увеличения числа реализации случайной величины (числа опытов). Повышение доверительной вероятности при сохранении доверительного интервала также требует увеличения числа реализаций. Но уве­личение числа реализаций случайной величины вызывает увели­чение компьютерного времени. Поэтому следует стремиться не просто к высокой точности результатов, а к целесообразным точ­ности и достоверности. В каждом конкретном случае моделирова­ния могут быть свои признаки целесообразной точности и досто­верности моделирования. Наиболее распространенные из них сле­дующие.

1. Среднеквадратическая ошибка результата из-за ограничен­ности реализаций не должна превышать половины суммарной среднеквадратической ошибки результата, вызванной другими факторами.

2. Доверительный интервал вероятности не должен превышать следующих пределов:

где p* — частность случайной величины; N — число реализаций, которое должно быть не меньше

где p*— вероятность воспроизводимой случайной величины; (р — р*)— допустимая ошибка.

3. Доверительный интервал для математического ожидания случайной величины

где D* (x)— дисперсия величины х, полученная из опыта.

Отсюда число реализации N должно быть не меньше числа

где М(х) – М*(х) — допустимая ошибка.

Способы воспроизведения процесса функционирования. При воспроизведении процесса функционирования исследуемого ЭА возможно использование двух способов.

1. Разбиение процесса функционирования на интервалы, рав­ные ∆ t. В конце каждого из таких интервалов анализируется со­стояние исследуемого объекта и запоминаются числа возникших состояний, используемых затем для обработки. Достоинство этого метода — возможность воспроизводить в модели непрерывные де­терминированные и случайные процессы. Недостаток — большая затрата компьютерного времени при моделировании сложных ЭА.

2. Использование характерных точек моделируемого процес­са. При этом способе процесс моделирования осуществляется фор­мированием моментов возникновения события, подлежащего уче­ту (момент возникновения отказа и т. п.). Время возникновения таких событий и их число запоминаются, и на основании их обра­ботки получаются требуемые характеристики. Этот способ назы­вают моделированием с независимым временем.

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. В чем основное отличие сложного ЭА от простого?

2. Что такое функциональная избыточность ЭА?

3. Перечислите характерные особенности, присущие сложным ЭА.

4. Какие функции выполняют иерархические СУ сложными ЭА?

5. Расскажите об алгоритме расчета функциональной надежности ЭА.

6. Поясните составляющие функционала оптимизационной задачи при обосновании требований к надежности оборудования сложного ЭА.

7. Дайте характеристику зависимости стоимости разработки и изготов­ления сложного ЭА от его надежности.

8. Как связаны стоимость сложного ЭА и его надежность на этапе экс­плуатации?

9. Каков порядок нахождения значений оптимальной надежности от стоимости сложного ЭА?

10. Какие вы знаете методы оптимизации?

11. В чем суть определения оптимального распределения значений надеж­ности элементов ЭА по стоимости на основании метода Лагранжа?

12. В каких случаях целесообразно решать задачу нахождения опти­мальных характеристик надежности элементов ЭА по стоимости ме­тодом имитационного моделирования?

13. Расскажите о содержании метода моделирования процесса функцио­нирования ЭА на компьютере.

14. Какова последовательность подготовки и моделирования надежно­сти сложных ЭА на компьютере?

15. Как производится моделирование случайных событий при оценке надежности сложных ЭА?

16. Объясните содержание решения задачи получения случайных чисел с заданными законами распределения при анализе надежности ЭА.

17. Назовите основные факторы, приводящие к возникновению ошибок в процессе моделирования и расчета надежности ЭА.

18. Какие вы знаете методы оценки точности и достоверности моделиро­вания надежности ЭА?

19. Расскажите, как подсчитывается количество требуемых реализа­ций случайных величин при моделировании надежности ЭА на ком­пьютере.

 

РАЗДЕЛ ТРЕТИЙ

⇐ Предыдущая31323334353637383940Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: