Определительные испытания на надежность

Признаком определительных испытаний является то, что в результате определяются количественные значения показателей надежности испытанных объектов. Однако по методам проведе­ния и способам обработки результатов, а также по планам органи­зации и условиям, в которых испытания проводятся, они могут быть различными (рис. 9.1).

Усредненные показатели обычно дают достаточное для прак­тических целей представление о надежности объекта, особенно тогда, когда необходимо произвести либо сравнение объектов, либо сравнение конструктивных вариантов. Однако среднее значение случайной величины не дает полного о ней представления. Более

подробную информацию о надежности можно получить по дове­рительному интервалу — интервалу возможных значений пока­зателя надежности, которым накрывается определенный показа­тель с заданной вероятностью.

Косвенными признаками назревающего отказа может быть выделение избыточного тепла, изменения токов и т. д. Принцип накопления информации заключается в том, что информация со­бирается из различных источников. Каждое последующее испы­тание служит для уточнения показателя надежности с использо­ванием априорной информации.

Ускорение испытаний имеет важное значение, так как глав­ный недостаток испытаний на надежность — их большая продол­жительность.

По планам проведения испытания делятся на следующие ос­новные группы: [NUN], [NUT], [NUr], [NU(r, T)], [NRT], [NRr], [NR(r, T)], [NMT], [NMr] и др.

Буквы указывают следующие особенности объектов: N — чис­ло одновременно испытываемых объектов; U — восстанавливае­мые и незаменяемые при испытаниях в случае отказа объекты; R — восстанавливаемые, но заменяемые при испытаниях в случае отказа объекты; М — восстанавливаемые при испытаниях в слу­чае отказа объекты; r — число отказавших объектов.

При испытаниях по плану [NUM] на испытания ставятся N объектов. Испытания ведутся до отказа всех объектов. Время от­каза t_i фиксируется.

Средняя наработка на отказ

Среднеквадратическое отклонение σ(Т₀) относительно его среднего значения

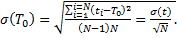(9.1)

При числе N, равном 8 и более, и при t_i вероятности безотказ­ности подчиняющихся экспоненциальному закону, распределение случайной величины Т с достаточной для практики точностью приближается к нормальному распределению. Поэтому число ис­пытываемых объектов можно определять из выражения (9.1).

Для экспоненциального закона σ(t) = Т_о. Из выражения

следует

(9.2)

Продолжительность испытаний можно определить по задан­ной вероятности того, что объект, поставленный на испытание, откажет. Вероятность возникновения отказа при экспоненциаль­ном законе распределения и продолжительность испытаний t_u со­ставляют:

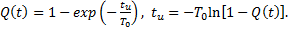(9.3)

Нетрудно видеть, что испытания по плану [NUM] требуют зна­чительного времени и количества объектов. Например, при испы­тании контакторов на коммутационную износостойкость преду­сматривается, согласно ТУ, до 1 млн циклов ВО, а на механиче­скую износостойкость — несколько миллионов. Это значительно усложняет получение срочной информации о работоспособности ЭА. В практике известны ускоренные методы испытания. Они при­меняются в тех случаях, когда на основании статистической обра­ботки большого числа результатов имеется возможность сопоставления параметров ускоренных испытаний с их допустимыми пре­делами.

В работе А. М. Залеского установлена зависимость, характери­зующая коммутационный износ контактов от значения тока на­грузки с учетом типа конструкторской разработки контактного узла, технологического процесса изготовления и сборки:

где т, т_н — потери массы контактной пары, соответствующие рабочему току и номинальному; N, N_H — число коммутационных операций, соответствующих указанным токам; п — показатель, зависящий от конструкторской разработки и качества изготовле­ния контактного узла.

Критерием средней наработки до предельного состояния для обоих режимов испытаний является контактирование по материа­лу контактодержателя. Следовательно, для допустимых пределов можно положить т = m_H. Отсюда число коммутационных опера­ций при будет соответствовать

Однако показатель средней наработки на отказ или среднее время безотказной работы требует равнозначности соответствую­щих испытаний на надежность. Ставится задача сохранить физи­ческую модель отказов при возрастании нагрузок. Это возможно при предположении о сохранении закона распределения отказов, т. е. закона, который обусловливает отношение равнозначности. В понятие отношения равнозначности испытаний вкладывается связь между временем количества коммутационного цикла t од­ного режима нагрузок I_н со временем количества коммутацион­ного цикла τ другого режима нагрузок I. Найденное аналитиче­ское выражение отношения равнозначности подставляется в усло­вия равенства надежности

(9.4)

Соотношение (9.4) тоже является отношением равнозначности. Для экспоненциального закона, где надежность Р = exp(-λt), отношение равнозначности будет

Отсюда при ускоренных испытаниях

Для закона распределения Вейбулла имеем

(9.5)

где с, β, γ — параметры закона Вейбулла.

Для испытуемого изделия без начального износа γ будет рав­няться нулю. Параметр β — формальный, значение которого при­нимается в пределах от 1 до 4. Отношение равнозначности будет иметь вид

Постоянные k и т задаются параметрами закона Вейбулла:

С другой стороны — из условия среднего времени безотказности работы следует

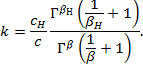
Таким образом, сократить продолжительность испытаний мож­но путем увеличения числа испытуемых изделий или снижения требований к точности результатов.

Применение восстановления отказавших объектов позволяет увеличить информативность испытаний без увеличения числа ис­пытываемых объектов.

Средняя наработка на отказ при испытаниях по плану [ NRr ], т. е. при постановке на испытания N объектов с восстановлением, до получения r отказов

(9.6)

где t_PΣ — суммарная наработка испытываемых объектов.

При отсутствии учета времени на восстановление

(9.7)

где t_r — время фиксации последнего отказа.

Для определения числа испытываемых объектов можно вос­пользоваться следующим методом. Так как среднеквадратическое отклонение наработки на отказ

где t — случайная величина (время до отказа); N — число испыта­ний, то ошибка определения в долях от

(9.8)

где значение Z_a при нормальном законе равно числу средних квадратических отклонений, которое нужно отложить от центра рас­сеяния для того, чтобы вероятность попадания в полученный уча­сток была равна а. Из (9.6) число испытаний составит

(9.9)

Таким образом, для планирования числа N необходимо задать точность ε и знать хотя бы ориентировочно величину σ(t). Если о величине σ(t) ничего не известно, тогда на испытание ставится чис­ло объектов N исходя из возможностей производства, a σ(t) опре­деляется в ходе испытания. По полученным значениям σ(t) уточ­няется число N.

Проведение испытаний по плану [ NRr ]уменьшает число ис­пытываемых N за счет их восстановления, но удлиняет время ис­пытаний. Увеличение числа испытываемых объектов при испы­таниях по плану [ NUM ]повышает точность результатов испыта­ний, а по плану [ NUr ], сокращает время испытаний.

 

9.3.

⇐ Предыдущая32333435363738394041Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: