 |
Общие правила комбинаторики.
|
|
|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ И КОНТРОЛЬНЫХ РАБОТ
по дисциплине Теория вероятности и математическая статистика
студентами, обучающимися по направлениям
080100.62 Экономика Мировая экономика
080100.62 Экономика Финансы и кредит
230700.62 Прикладная информатика Прикладная информатика в экономике
экономического факультета
Дата ввода –__ ___________2011г., протокол № 1
Дата изменения – ___ ________2014г., протокол № 1
Уфа - 2014г.
Составитель: Муллабаева А.У..
Методические указания по курсу «Теория вероятности и математическая статистика» для студентов очной и заочной формы обучения / Российский экономический университет им. Г.В.Плеханова Уфимский институт.
Методические указания предназначены для студентов очной и заочной формы обучения направлений 080100.62 Экономика - Мировая экономика, 080100.62 Экономика - Финансы и кредит, 230700.62 Прикладная информатика - Прикладная информатика в экономике УИ РЭУим. Г.В.Плеханова. Методические указания соответствуют учебному плану и государственному общеобразовательному стандарту. Полученные по данному предмету знания являются основой для овладения другими дисциплинами специализации.
Рецензенты:
Оглавление
ВВЕДЕНИЕ.. 4
§1. Элементы комбинаторики. 6
§2. Основные понятия теории вероятностей. 8
§3. Теоремы сложения и умножения вероятностей. 11
§4. Формула полной вероятности. Формула Байеса. 14
§5. Формула Бернулли. 16
§6. Локальная теорема Лапласа. 18
§7. Интегральная теорема Лапласа. 19
§8. Формула Пуассона. 21
§9. Дискретные случайные величины. 22
§10. Числовые характеристики дискретной случайной величины.. 24
§11. Непрерывные случайные величины. 27
|
|
|
§ 12 Равномерное и нормальное распределения. 34
§14. Эмпирическая функция распределения. 40
§15. Полигон и гистограмма. 42
§16. Точечные оценки. 47
§17. Интервальные оценки. 51
§18. Решение типовых задач по математической статистике. 54
§19. Элементы теории корреляции. 59
Задачи контрольной работы для студентов заочной формы обучения. 63
КОНТРОЛЬНЫЕ ВОПРОСЫ... 81
Вопросы для подготовки к экзамену. 85
Варианты индивидуальных заданий для студентов очного отделения. 95
Примерная тематика докладов. 118
Литература. 119
Приложения. 120
ВВЕДЕНИЕ
Цель и задачи дисциплины
Курс «Теория вероятностей и математическая статистика» является составной частью цикла математических дисциплин, составляющих фундамент математического образования специалиста. В любой области человеческой деятельности имеют место случайные явления, которые не позволяют осуществить точный прогноз результатов этой деятельности. Теория вероятностей и математическая статистика изучают закономерности случайных явлений. Знание этих закономерностей помогает принимать решения в условиях неопределённости, направленные на достижение поставленных целей.
Курс «Теория вероятностей и математическая статистика» является основой для изучения последующих дисциплин, таких как «Эконометрика», «Статистические методы прогнозирования», «Исследование операций», «Методы оптимизации», «Теория массового обслуживания», «Теория восстановлений», «Основы актуарных расчётов» и т.д.
Преподавание теории вероятностей и математической статистики имеет целью: ознакомить студентов с основами теории, необходимыми для решения прикладных задач, развить способности студентов к логическому и алгоритмическому мышлению, привить навыки самостоятельного изучения литературы по данной дисциплине и ее приложениям. На практических занятиях по дисциплине необходимо развить навыки составления и анализа математических моделей несложных задач прикладного характера, связанных со случайными явлениями, научить способам вычисления вероятностей простых и сложных событий, методам оценки неизвестных параметров на основе экспериментальных данных, методам проверки гипотез и правилам принятия решений, методам аппроксимации статистических связей между величинами или факторами.
|
|
|
Приступая к изучению курса теории вероятностей и математической статистики, студент должен знать:
элементарную математику в объёме средней школы;
дифференцирование и интегрирование функций из курса высшей математики;
основные сведения по сбору и первичной обработке данных из общего курса статистики.
Методические указания включают задания для выполнения работ на практических занятиях и варианты заданий для проведения текущего контроля для студентов очного отделения и задания домашнего выполнения, перечень вопросов на экзамен для студентов заочного обучения.
В каждом параграфе приведены примеры, пояснение изучаемого вопроса. Надеемся, что рассмотрение этих примеров поможет студентам при решении контрольных заданий.
Задачи контрольных работ для студентов заочного отделения одного варианта оканчиваются на одну и ту же цифру, совпадающую с последней цифрой номера зачетной книжки. Например, если номер зачетной книжки оканчивается на 6, то все задачи № 06, 16, 26,… входят в контрольную работу варианта № 6.
При оформлении контрольной работы решение задач следует излагать по порядку, подробно, предварительно полностью переписав задание. Работа оформляется на 12 листовой тетрадке в клетку.
Элементы комбинаторики
Общие правила комбинаторики.
Рассмотрим k множеств М 
, М 
, М 
, …, М 
, содержащих по m 
, m 
, m 
,…, m 
элементов соответственно. Выбирается по одному элементу из каждого множества и составляется еще одно множество. Число способов, которыми можно выбрать по одному элементу из каждого множества, равно произведению m ∙ m ∙ m ∙…∙ m . В этом и состоит основной принцип произведения комбинаторики.
В задачах теории вероятностей часто рассматриваются различные соединения (комбинации) k элементов из множества, содержащего n элементов (k≤n). Будем рассматривать такие соединения, в которые каждый элемент данного множества может входить не более одного раза, то есть соединения без повторений. Рассмотрим три вида соединений: размещения, перестановки, сочетания.
|
|
|
Определение. Размещениями из n элементов по k элементов называются наборы k элементов, отличающиеся один от другого или самими элементами (составом элементов), или их порядком. Число размещений обозначается A 
.
Число размещений из n элементов по k элементов находится по формуле:
А 
=n∙(n–1)∙(n–2)∙…∙(n–(k–1)). (1)
Определение. Перестановками из данных n элементов называются наборы из n элементов, различающихся только порядком.
Перестановки – это частный случай размещений. Число всех перестановок обозначают символом Р 
. Число Р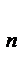 
найти несложно. Для этого в формулу (1) подставляем k=n.
Р 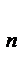=n∙(n–1)∙(n–2)∙…∙(n–(k–1))∙…∙2∙1=n!
Определение. Произведение n первых натуральных чисел называется факториалом числа n и обозначается символом n!(читается «эн факториал»).
Р 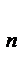=1·2·3 …∙n=n! (2)
Приведем некоторые значения факториала:
0!=1, 5!= 1·2·3·4∙5=120,
1!=1, 6!= 1·2·3·4∙5∙6=720,
2!=1·2=2, 7!= 1·2·3·4∙5∙6∙7=5040,
3!=1·2·3=6, 8!= 1·2·3·4∙5∙6∙7∙8=40320,
4!=1·2·3·4=24, 9!= 1·2·3·4∙5∙6∙7∙8∙9=362880.
Определение. Сочетаниями, содержащими k элементов, выбранных из n элементов заданного множества, называются всевозможные наборы k элементов, различающиеся хотя бы одним элементом. Число сочетаний из n элементов по k элементов обозначают С или (
.
Число сочетаний из n элементов по k элементов определяется формулой:
С = 
Примеры решения задач.
1. Определить, сколько трехзначных чисел можно составить из множества цифр 7,8,9,3,2 без повторений.
Решение. Трехзначные числа можно рассматривать как размещения, так как при замене одной цифры другой или перестановке их местами получаются разные числа. Так как n=5, k=3, то различных чисел будет:
А 
=5·4·3=60.
2. К кассе за получением (или для уплаты) денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь?
|
|
|
Решение. Очередь состоит из 4 различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из четырёх человек, их число равно:
Р4 = 4! = 24. 
3.В цехе 18 человек, из них 10 мужчин. На конференцию отбирают 6 человек так, что было 3 мужчины и 3 женщины. Сколько различных списков можно составить?
Решение. 3-х мужчин из 10 человек можно отобрать С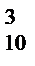 
различными способами, 3-х женщин из 8 можно отобрать С 
различными способами. Следовательно, 3-х женщин и 3-х мужчин можно отобрать С 
· С 
– различными способами.
Найдем: С = 
= 
,
С = 
= 
.
Итого, число различных списков:
С ∙ С = 120 · 54 = 6480.
Основные понятия теории вероятностей
Определение. Результат некоторого опыта или эксперимента, который нельзя заранее предсказать назовем случайным событием.
События обозначаются большими латинскими буквами: А, В, С,…
Примеры наиболее часто встречающихся испытаний и событий приведены в таблице.
Определение. Достоверным назовем событие, которое обязательно произойдет в результате опыта.
Например, из урны с 20 красными шарами обязательно будет вынут красный шар.
Определение. Невозможным назовем событие, которое заведомо не произойдет в результате опыта.
Например, из урны с 20 красными шарами не будет вынут зеленый шар.
| Испытания | События |
| 1. Бросание монеты. 2. Бросание игральной кости. 3. Извлечение карты из колоды. 4. Извлечение шара из урны. 5. Стрельба по мишени. 6. Учащийся отвечает на вопросы теста. 7. Сажаются семена томата определённого сорта. | 1. Выпал герб (орёл); выпала цифра (решка). 2. Выпало 5 очков; выпало 3 очка; выпало чётное число очков; выпало не менее 3-х очков,... 3. Извлекли бубновую карту; достали туза; вытащили даму пик; извлекли не старше дамы, … 4. Извлекли белый шар; извлекли зелёный шар; вытащили шар с номером 2; … 5. Попадание, промах; выбито 9 очков, … 6. Правильно ответил на все вопросы; на половину вопросов; хотя бы на один вопрос, … 7. Взойдут 9 семян; все взойдут; взойдет не менее 5 семян, … |
| Очевидно, что ряд таких примеров можно продолжать долго. В разряд испытаний можно отнести процессы, с которыми сталкиваемся достаточно регулярно, например: наблюдение за погодой (здесь событиями являются – ясный день, дождь, снег, ветер и т.д.); выход на работу в определенный день (приход на работу вовремя; опоздание; отгул и т.д.); нахождение в неблагоприятных условиях, при которых можно получить некоторое заболевание (заразиться гриппом; простыть на сквозняке; получить профзаболевание или травму на производстве и т.д.) |
|
|
|
Определение. События А и В называются несовместными, если появление одного из них исключает появление другого, в противном случае события называются совместными.
Рассмотрим пример. События: А – из колоды вынута крестовая карта, В – из колоды вынута бубновая карта, D – из колоды вынута дама.
События А и В – несовместные. События А и D – совместные, так как из колоды может быть вынута дама крестей, в этом случае произойдет и событие А – крестовая карта, и событие D – дама.
Определение. События А и 
называются противоположными, если событие происходит всякий раз, когда не происходит событие А и наоборот.
Например, событие А –выпал герб при бросании монеты и событие – выпала цифра– противоположное.
Определение. События называются равновозможными, если нет основания считать, что одно из них произойдет скорее, чем другое.
Определение. Элементарными событиями назовем все результаты испытания, которые являются попарно несовместными и равновозможными. Те элементарные события, в которых наступает событие А, назовем благоприятствующими появлению события А.
Определение. Вероятностью события А (обозначается Р(А)) называется отношение числа m благоприятствующих исходов к общему числу n элементарных исходов опыта (классическое определение вероятности).
Итак, вероятность события А определяется формулой:
Р(А)= 
,
где m – число элементарных событий, благоприятствующих событию А, n – число всех элементарных исходов испытания.
Например, в урне 10 красных и 7 зеленых шаров, достаем 1 шар. Рассмотрим события: А – из урны вынут красный шар, В – из урны вынут зеленый шар. Найдём вероятности этих событий.
Решение: всего в урне 17 шаров, тогда n = 17. Благоприятствующими исходами для события А будет извлечение любого из 10 красных шаров, то есть m = 10, таким образом Р(А)= 
; аналогично, Р(В)= 
.
Пример. На конференцию из группы студентов из 20 человек (8 девушек, 12 юношей) отбирают 5 человек. Найти вероятность следующих событий:
А – среди отобранных студентов одни юноши,
В – среди отобранных студентов одни девушки,
С – среди отобранных 2 девушки и 3 юношей.
Решение. Заметим, что общее число исходов для всех трех событий будет одинаковым n= C 
.
Число благоприятствующих исходов: mА = C 
, mВ = C 
, mС = C 
∙С 
.
Следовательно, получаем вероятность появления события А:
Р(А)= 
= 
= 
=
= 
= 
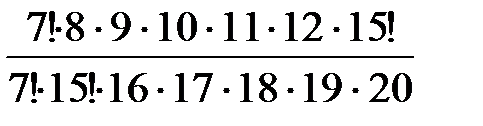= 0,051.
Найдем вероятность появления события В.
Р(В)= 
= 
= 
= 
= 
=0,006
Аналогично получаем:
Р(С)= 
= 
= 
= 
=
= 
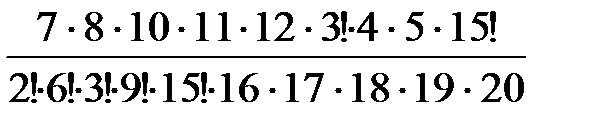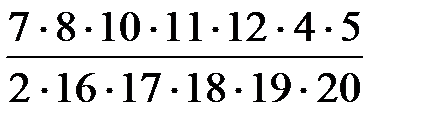= 0,0795.
Заметим, что вероятность достоверного события равна 1, а вероятность невозможного равна 0. Вероятность случайного события А заключена между 0 и 1. Итак, для любого события верно неравенство: 0 ≤ Р(А) ≤ 1.
|
|
|
