 |
Задания для самостоятельной работы
|
|
|
|
1. Плотность распределения случайной величины Х задана функцией
 .
.
Найти:
1) значение параметра с; 2) найти функцию распределения  ;
;
3) построить графики функций  и
и  ;
;
4) найти математическое ожидание случайной величины;
5) найти дисперсию случайной величины.
2. Случайная величина Х задана функцией распределения
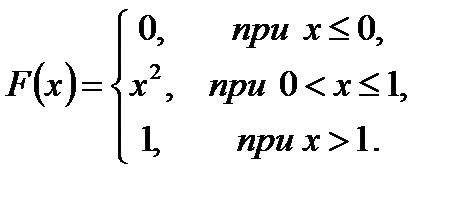
Найти:
1) найти плотность распределения  ;
;
2) построить графики функций  и
и  ;
;
3) найти математическое ожидание случайной величины;
4) найти дисперсию случайной величины;
5) найти вероятность того, что случайная величина принимает значение из интервала  .
.
Тема 8. Основные типы распределений непрерывных случайных величин.
Вопросы для самопроверки
1. Какие виды распределений непрерывных случайных величин знаете?
2. Что такое равномерное распределение?
3. Выведите числовые характеристики равномерного распределения.
4. Охарактеризуйте показательное распределение.
5. Какое распределение называют нормальным?
6. Что называют интегралом Лапласа?
7. Как, пользуясь таблицей значений интеграла Лапласа, вычислить вероятность попадания нормально распределённой случайной величины в некоторый интервал?
Задания для самостоятельной работы
1. Даны функции:  ; 2)
; 2)  ; 3) f3 (x) =
; 3) f3 (x) =  .
.
Являются ли эти функции плотностями вероятности?
2. Если соблюдается график движения, то среднее время ожидания пассажиром трамвая равно 3,5 минуты. Известно, что время ожидания имеет равномерный закон распределения. Минимальное время ожидания равно 0. Найти вероятность того, что пассажир будет ожидать трамвай от двух до пяти минут.
3. Время ремонта и обслуживания автомобиля после одной поездки случайно и имеет экспоненциальный закон распределения. Было замечено, что в текущем сезоне на ремонт и обслуживание автомобиля после одной поездки тратилось в среднем 5 минут. Найти вероятность того, что при очередной поездке это время не превысит 30 минут.
|
|
|
4. Рост взрослого мужчины удовлетворительно описывается нормальным законом распределения. По статистике средний рост составляет 175 см, а среднеквадратическое отклонение равно 7 см. Найти вероятность того, что рост наугад взятого мужчины будет отличаться от среднего роста не больше чем на 7 см.
5. Случайная величина распределена нормально. Найти  , если
, если
 , а
, а  .
.
6. Случайная величина распределена нормально. Найти  , если
, если
 .
.
Тема 9. Числовые характеристики случайных величин.
Вопросы для самопроверки
1. Что такое начальные и центральные моменты различных порядков?
2. С какими моментами связаны математическое ожидание и дисперсия?
3. С помощью каких числовых характеристик описывается отличие конкретного распределения от нормального?
4. Что такое мода, медиана?
5. Что характеризует эксцесс?
Задания для самостоятельной работы
1. Страховая компания заключает однотипные договоры, причём страховая премия (сумма, выплачиваемая страховщиком при заключении договора) составляет 4 тыс. рублей. При наступлении страхового случая компания должна выплатить 20 тыс. рублей. Известно, что страховой случай наступает в 4% случаев. Фирме удалось застраховать 200 клиентов. Ответить на вопросы:
а) Каков средний доход фирмы и среднеквадратическое отклонение дохода фирмы?
б) Какова вероятность того, что доход фирмы будет находиться в пределах от 710 до 750 тыс. рублей?
Тема 10. Системы случайных величин.
Вопросы для самопроверки
1. Что такое двумерная случайная величина?
2. Как задается функция распределения двумерной случайной величины?
3. Что такое ковариация случайных величин?
4. Что такое коэффициент корреляции случайных величин? Перечислите основные свойства коэффициента корреляции.
|
|
|
5. Что такое условное математическое ожидание?
6. Объясните, как построить линию регрессии Y на Х.
|
|
|


