 |
Формула полной вероятности. Формула Байеса
|
|
|
|
Определение. Будем говорить, что события В 
, В 
, …, В 
образуют полную группу событий, если:
1. Событие В + В + …+ В достоверное;
2. События Вi и Вj – попарно несовместные (i= 1,2,…,n, j= 1,2,…,n, i 
j).
Утверждение. Сумма вероятностей событий, образующих полную группу равна 1.
Пример. Студент на экзамене может получить одну из четырех оценок: «отлично», «хорошо», «удовлетворительно» и «неудовлетворительно». События 
– получил «отлично»,
– получил «хорошо»,
– получил «удовлетворительно»,
– получил «неудовлетворительно»
попарно несовместные и в сумме – событие достоверное, так как обязательно происходит одно из этих событий. Следовательно, события В , В , В 
, В4 образуют полную группу событий.
Для нахождения вероятности события А, которое может произойти при условии осуществления одного из несовместных событий В , В , …, В , образующих полную группу, используется формула:
Р(А)= 
Эта формула называется формулой полной вероятности.
События В , В , …, В называются гипотезами.
Пример. В урну, содержащую два шара, опущен зеленый шар. Найти вероятность того, что будет вытащен из урны зеленый шар, если равновероятны первоначальные представления о цвете шаров.
Решение. Событие А– извлечен зеленый шар.
Возможны следующие гипотезы о первоначальном составе шаров:
В – первоначально зеленых шаров не было в урне;
В – был 1 зеленый шар;
В 
– оба шара зеленые.
По условию задачи гипотезы равновероятны и образуют полную группу событий, следовательно, вероятность каждой из гипотез равна ⅓, то есть Р(В )= Р(В ) = Р(В 
) = ⅓. Тогда условные вероятности наступления события А при появлении каждой из гипотез будут соответственно равны:
|
|
|
Р 
(А) = ⅓; Р 
(А) = ⅔; Р 
(А) =1.
Отсюда по формуле полной вероятности получаем:
Р(А) = Р(В 
) · Р (А) + Р(В 
) · Р (А) + Р(В 
) · Р (А).
Р(А) = ⅓ · ⅓ + ⅓ · ⅔ + ⅔ · 1 = ⅔.
Пусть событие А может наступить лишь при условии появления одного из несовместных событий В 
, В 
, …, В 
, образующих полную группу событий.
Если событие А уже произошло, то вероятности гипотез В , В , …, В могут быть переоценены по следующей формуле:
Р 
(B 
)= 
,
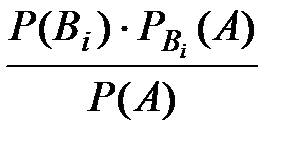где i = 1, 2, 3,…, n.
Эта формула называется формулой Байеса.
Пример. Два автомата производят одинаковые детали, поступающие на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй 84%. Наудачу взятая деталь оказалась отличного качества. Найти вероятность того, что эта деталь сделана первым автоматом.
Решение. Рассмотрим событие А – деталь отличного качества.
Можно составить две гипотезы:
В 
– деталь сделана первым автоматом, причем Р(В 
) = ⅔, так как его производительность вдвое больше производительности второго автомата.
В 
– деталь сделана вторым автоматом, причем Р(В 
) = ⅓.
Условная вероятность появления события А при выполнении гипотезы В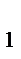 
равна Р (А) = 0,6.
Условная вероятность появления события А при выполнении гипотезы В равна: Р (А) = 0,84.
Отсюда вероятность появления события А равна:
Р(А) = ⅔ · 0,6 + ⅓ · 0,84 = 0,68.
Тогда вероятность того, что деталь отличного качества сделана первым автоматом, по формуле Байеса равна:
Р 
(В 
) = 
= 
.
Формула Бернулли
Пусть производится n независимых испытаний, в каждом из которых событие может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р (0< p < 1). Следовательно, вероятность непоявления события А в каждом испытании также постоянна и равна q = 1 – p.
Часто возникает задача вычислить вероятность того, что при n испытаниях событие А наступит ровно k раз.
|
|
|
Искомая вероятность обозначается P 
(k).
Например, символ Р 
(3), означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
Поставленную задачу можно решить с помощью так называемой формулы Бернулли.
P 
(k) = 
,
где 
.
Вероятности того, что в n испытаниях событие наступит: а)менее t раз; б) более t раз; в) не менее t раз; г) не более t раз находят соответственно по формулам:
a) P (0) + P (1)+…+ P (t–1)= P (k<t),
б) P (t+1) + P (t+2) + … + P (n) = P (k>t),
в) P (t) + P (t +1) + … + P (n) = P (k≥t),
г) P (0) + P (1) +… + P (t) = P (k≤t).
Пример. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р=0,7. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии в продолжении каждых из 6 суток постоянна и равна р=0,7. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q =1 – p = 1 – 0,7 = 0,3.
Из условия задачи следует, что n = 6; k=4.
Искомая вероятность по формуле Бернулли равна:
.
Локальная теорема Лапласа
Формула Бернулли позволяет вычислить вероятность того, что событие появиться в n испытаниях ровно k раз: P (k) = 
При применении формулы учитывается, что вероятность появления события в каждом испытании постоянна. Легко видеть, что пользоваться формулой Бернулли при больших значениях n достаточно трудно.
Естественно, возникает вопрос: нельзя ли вычислить интересующую нас вероятность, если число испытаний велико, не прибегая к формуле Бернулли? Оказывается, можно.
Локальная теорема Лапласа и дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в n испытаниях, если число испытаний достаточно велико.
Локальная теорема Лапласа.
Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р 
(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n):
Р (k) = 
где 
φ(x) = 
; q = 1 – p.
Имеются таблицы, в которых помещены значения функции φ(x)= 
,
|
|
|
соответствующие положительным значениям аргумента x (см. приложение 1).
Для отрицательных значений аргумента пользуются теми же таблицами, так как φ(х) – функция четная, то есть φ(–x) = φ(x).
Пример. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании
равна 0,2.
Решение. По условию, n=400; k=80; p=0,2; q=0,8.
Воспользуемся формулой Лапласа:
Р 
(80)≈ 
.
Вычислим определяемое данными задачи значение х:
x = (k–np) / 
= (80 – 400 ∙ 0,2) / 8 = 0
По таблице приложения 1 находим φ(0)=0,3989.
Искомая вероятность:
Р 
(80)= (1/8)∙0,3989=0,04986.
Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены): Р (80)=0,0498.
|
|
|
