 |
Эмпирическая функция распределения
|
|
|
|
Пусть известно статистическое распределение частот количественного признака Х. Введем обозначения:  ─ число наблюдений, при которых наблюдалось значение признака, меньше х; n – общее число наблюдений (объем выборки). Ясно, что относительная частота события Х<х равна
─ число наблюдений, при которых наблюдалось значение признака, меньше х; n – общее число наблюдений (объем выборки). Ясно, что относительная частота события Х<х равна  . Если х изменяется, то, вообще говоря, изменится и относительная частота, то есть относительная частота
. Если х изменяется, то, вообще говоря, изменится и относительная частота, то есть относительная частота  есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.
есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.
Определение. Эмпирическая функция распределения (функция распределения выборки) – функция F*(x), определяющая для каждого значения х относительную частоту события X<x.
 ,
,
где  ─ число вариант, меньших х; n – объем выборки.
─ число вариант, меньших х; n – объем выборки.
Например, для того чтобы найти F*(x2), надо число вариант, меньших x2, разделить на объем выборки:
 .
.
В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(x) определяет вероятность события X<x, а эмпирическая функция F*(x) определяет относительную частоту этого же события.
Из теоремы Бернулли следует, что относительная частота события X<x, то есть F*(x), стремится по вероятности к вероятности этого события, то есть к значению F(x). Другими словами, при больших значениях n числа F*(x) и F(x) мало отличаются одно от другого в том смысле, что  . Уже отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности. Такое заключение подтверждается и тем, что F*(x) обладает всеми свойствами F(x).
. Уже отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности. Такое заключение подтверждается и тем, что F*(x) обладает всеми свойствами F(x).
|
|
|
Из определения функции F*(x) вытекают следующие ее свойства:
1) Значения эмпирической функции принадлежит отрезку [0; 1];
2) F*(x) – неубывающая функция;
3) Если x1 ─ наименьшая варианта, то F*(x) = 0 при х < х1;
если хk ─ наибольшая варианта, то F*(x) = 1 при х > xk.
Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
Пример. Построить эмпирическую функцию по данному распределению выборки:
Варианты 
| |||
Частоты 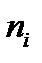
|
Решение. Найдем объем выборки (сумма всех частот ni):
n = n1 + n1 + n1 = 12 + 18 + 30 = 60.
Наименьшая варианта равна 2 (x1 = 2), следовательно, F*(x) = 0 при х ≤ 2 (по свойству 3 функции F*(x));
значения, меньшие 6 (х<6), а именно x1 = 2, наблюдались n1 = 12 раз, следовательно,  при 2<x≤6;
при 2<x≤6;
значения х<10, а именно x1 = 2, x1 = 2 наблюдались n1 + n2 = 12 + 18 = 30 раз, следовательно  при 6<х≤10.
при 6<х≤10.
Так как х =10 – наибольшая варианта, то F*(x) = 1 при х>10 (по свойству 4 функции F*(x)).
Искомая эмпирическая функция имеет вид:
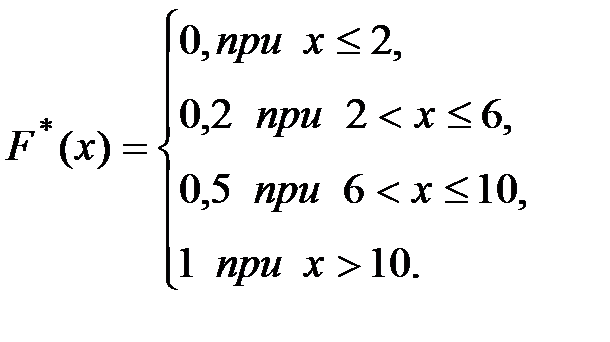
Ниже приведен график полученной эмпирической функции.
На графике на соответствующих осях откладывают значения функции F*(x) и интервалы вариант
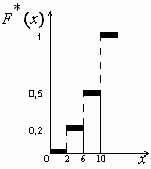
Рис. 5. График эмпирической функции.
Полигон и гистограмма
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Определение. Полигоном частот называют ломаную, отрезки которой соединяют точки (x1, n1), (x2, n2), …, (xk, nk).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni. Точки (xi, ni) соединяют отрезками прямых и получают полигон частот.
Определение. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x1, w1), (x2, w2), …, (xk, wk).
Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат wi. Точки (xi, wi) соединяют отрезками прямых и получают полигон относительных частот.
|
|
|
На рисунке изображен полигон относительных частот следующего распределения:
| x | 1,5 | 3,5 | 5,5 | 7,5 |
| w | 0,1 | 0,2 | 0,4 | 0,3 |
| Wi 0,4 0,3 0,2 0,1 0 0,5 2,5 5,5 7,5 xi |
Рис. 6. Полигон относительных частот.
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длинной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-ый интервал.
Определение. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению  (плотность частоты).
(плотность частоты).

Рис. 7. Гистограмма частот.
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс, на расстоянии  .
.
Площадь i-го частичного прямоугольника равна  =
= 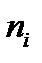 ─ сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, то есть объему выборки n.
─ сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, то есть объему выборки n.
На рисунке 2 изображена гистограмма частот распределения объема n=100, приведенного в таблице 1.
| Частичный интервал, длиною h=5 | Сумма частот вариант частичного интервала 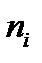
| Плотность частоты 
|
| 5 – 10 | 0,8 | |
| 10 – 15 | 1,2 | |
| 15 – 20 | 3,2 | |
| 20 – 25 | 7,2 | |
| 25 – 30 | 4,8 | |
| 30 – 35 | 2,0 | |
| 34 – 40 | 0,8 |
Определение. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длинною h, а высоты равны отношению  (плотность относительной частоты).
(плотность относительной частоты).
Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии  . Площадь i-го частичного прямоугольника равна
. Площадь i-го частичного прямоугольника равна  =
=  ─ относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.
─ относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.
Примеры.
1. В результате выборки получена следующая таблица распределения частот.
|
|
|

| |||
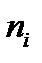
|
Построить полигоны частот и относительных частот распределения.
Для начала построим полигон частот.
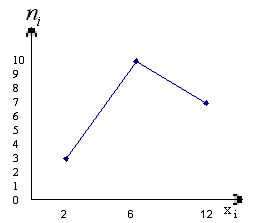
Рис. 8. Полигон частот.
Чтобы построить полигон относительных частот найдем относительные частоты, для чего разделим частоты на объем выборки n.
n = 3 + 10 + 7 = 20.
 .
.
Получаем

| |||

| 0,15 | 0,50 | 0,35 |
Построим полигон относительных частот.

Рис. 9. Полигон относительных частот.
2. Построить гистограммы частот и относительных частот распределения.
Найдем плотность частоты  :
:
| Частичный интервал, длиною h = 3 | Сумма частот вариант частичного интервала 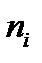
| Плотность частоты 
|
| 2 – 5 | ||
| 5 – 8 | 3,3 | |
| 8 – 11 | 8,3 | |
| 11 – 14 |
Построим гистограмму частот.

Рис. 10. Гистограмма частот.
Чтобы построить гистограмму относительных частот, нужно найти относительные частоты. Для этого найдем объем выборки n.
 .
.
Теперь найдем относительные частоты  :
:

Получим:
| Частичный интервал | Сумма относительных частот
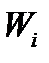
| Плотность частоты 
|
| 2 – 5 | 0,18 | 0,06 |
| 5 – 8 | 0,2 | 0,07 |
| 8 – 11 | 0,5 | 0,16 |
| 11 – 14 | 0,12 | 0,04 |
Плотности частот  нужно вычислить. При этом h = 3.
нужно вычислить. При этом h = 3.

Построим гистограмму относительных частот.
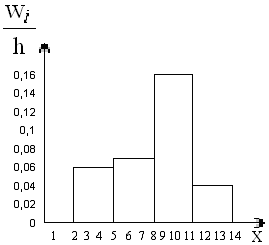
Рис.11. Гистограмма относительных частот.
Точечные оценки
Определение. Статистической оценкой Q* неизвестного параметра Q теоретического распределения называют функцию f(x1, x2, …, xn) от наблюдаемых случайных значений x1, x2, …, xn.
Определение. Точечной оценкой называют статистическую оценку, которая определяется одним числом Q* = f(x1, x2, …, xn), где x1, x2, …, xn ─ результаты n наблюдений над количественным признаком Х (выборка).
Определение. Несмещенной называют точечную оценку Q*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, то есть M(Q*) = Q. Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру.
Выборочная средняя.
Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.
|
|
|
Определение. Выборочной средней  называют среднее арифметическое значение признака выборочной совокупности.
называют среднее арифметическое значение признака выборочной совокупности.
Если все значения x1, x2, …, xn признака выборки объема n различны, то 
Если же все значения признака x1, x2, …, xk имеют соответственно частоты n1, n2, …, nk, причем n1 + n2 + … + nk = n, то
 ,
,
где  – объем выборки.
– объем выборки.
Выборочная средняя является несмещенной оценкой генеральной средней (неизвестного математического ожидания).
Замечание. Если первоначальные варианты  ─ большие числа, то для упрощения решения целесообразно вычесть из каждой варианты одно и то же
─ большие числа, то для упрощения решения целесообразно вычесть из каждой варианты одно и то же
число С, то есть перейти к условным вариантам ui = xi – c. Тогда
 .
.
Выборочная дисперсия.
Смещенной оценкой генеральной дисперсии служит выборочная дисперсия. Эту величину вводят для того, чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг среднего значения  .
.
Определение. Выборочной дисперсией  называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения  . Если значения признака x1, x2, …, xk имеют соответственно частоты n1, n2, …, nk, причем n1 + n2 + … + nk = n, то
. Если значения признака x1, x2, …, xk имеют соответственно частоты n1, n2, …, nk, причем n1 + n2 + … + nk = n, то

Эта оценка является смещенной, так как  ,
,
где DГ – генеральная дисперсия – среднее арифметическое квадратов отклонения значения признака генеральной совокупности от их среднего значения 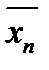 .
.
Теорема. Выборочная дисперсия равна среднему квадратов значений признака минус квадрат выборочной средней.

Для вычисления выборочной дисперсии эта формула наиболее удобна.
Замечание. Если перейти к условным вариантам ui = xi – c, то дисперсия при этом не изменится. Тогда  .
.
Оценка генеральной дисперсии по исправленной выборочной.
Пусть из генеральной совокупности в результате n независимых наблюдений
над количественным признаком Х извлечена повторная выборка объема n:
| Значения признака | xi | x1 | x2 | … | xk |
| Частоты | ni | n1 | n2 | … | nk |
При этом n1 + n2 + … + nk = n. Требуется по данным выборки найти неизвестную генеральную дисперсию DГ. Если в качестве оценки DГ принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение DГ. Объясняется это тем, что математическое ожидание выборочной дисперсии не равно оцениваемой DГ, а равно 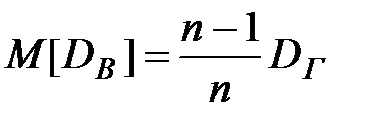 .
.
Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить  на дробь n/(n–1). Сделав это, мы получим исправленную дисперсию, которую обычно обозначают
на дробь n/(n–1). Сделав это, мы получим исправленную дисперсию, которую обычно обозначают  .
.
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:
|
|
|
 .
.
Более удобна форма:
 .
.
В условных вариантах она имеет вид:
 ,
,
причем если ui = xi – c, то  ; если
; если  , то
, то 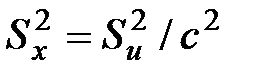 .
.
Задача 1.
Из генеральной совокупности извлечена выборка объемом n = 60

| ||||
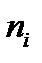
|
Найти несмещенную оценку генеральной средней.
Решение. Несмещенной оценкой генеральной средней является выборочная средняя:  ,
,
где  ─ варианта выборки,
─ варианта выборки, 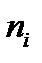 ─ частота варианты
─ частота варианты  ;
;  объем выборки.
объем выборки.
 .
.
Ответ: 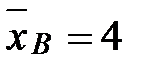 .
.
Задача 2.
|
|
|


