 |
Элементы теории корреляции
|
|
|
|
Определение. Зависимость двухслучайных величин называют корреляционной, если изменение одной случайной величины приводит к
изменению среднего значения другой случайной величины.
Основные задачи теории корреляции:
1. определить есть ли связь между случайными величинами, если есть, то найти уравнение зависимости (уравнение регрессии);
2. определить силу (тесноту) связи между случайными величинами.
Для определения самого факта связи между случайными величинами и тесноты связи служит коэффициент корреляции. Уравнение регрессии позволяет предсказать, какие изменения в среднем будет претерпевать признак при изменении другого признака.
Если уравнения регрессии являются линейными, то есть графиками будут прямые линии, то корреляционная зависимость называется линейной.
Выборочный коэффициент корреляции  находится по формуле:
находится по формуле:
 .
.
Свойства выборочного коэффициента корреляции:
1. Значения коэффициента корреляции изменяются на отрезке [–1;1]:
 .
.
2. Чем модуль  больше и ближе к 1, тем теснее связь между изучаемыми признаками.
больше и ближе к 1, тем теснее связь между изучаемыми признаками.
3. Если  , то между признаками функциональная связь.
, то между признаками функциональная связь.
4. Если  , то между изучаемыми признаками нет линейной корреляционной зависимости.
, то между изучаемыми признаками нет линейной корреляционной зависимости.
5. Если 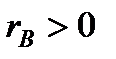 , то между признаками прямая (положительная) связь, если
, то между признаками прямая (положительная) связь, если  , то между признаками обратная (отрицательная) связь.
, то между признаками обратная (отрицательная) связь.
Выборочное уравнение прямой регрессии Y на X имеет вид:
 ,
,
где  ,
, 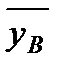 – выборочные средние, за приближенные значения σy и σx принимают соответственно sx и sy:
– выборочные средние, за приближенные значения σy и σx принимают соответственно sx и sy:
 ,
,  .
.
Выборочное уравнение прямой регрессии X на Y имеет вид:
 ,
,
Пример. Были произведены измерения общей длины ствола в см (X) и длины его части без ветвей (Y) 10 молодых сосен. Результаты этого измерения представлены в таблице:
|
|
|
| X | ||||||||||
| Y |
Вычислить выборочный коэффициент корреляции и найти выборочное уравнение прямой регрессии Y на X.
Решение. Вычислим выборочный коэффициент корреляции по формуле:

Для вычисления величин, входящих в формулу, составим вспомогательную таблицу (приведена на следующей странице), в которой результаты измерений записаны столбцами. Внизу каждого из столбцов вычислены суммы для нахождения средних  и
и  . Далее расположены столбцы, в которых вычисляются разности xi–
. Далее расположены столбцы, в которых вычисляются разности xi–  и yi–
и yi–  , их квадраты и произведения. Значения этих столбцов суммируются (последняя строка), чтобы получились величины, необходимые для подстановки в формулу. Отметим, что суммы в столбцах, в которых вычислены разности xi–
, их квадраты и произведения. Значения этих столбцов суммируются (последняя строка), чтобы получились величины, необходимые для подстановки в формулу. Отметим, что суммы в столбцах, в которых вычислены разности xi–  и
и
yi–  будут всегда равны нулю.
будут всегда равны нулю.
Находим средние  и
и  (смотри данные в таблице, 1–2 столбцы):
(смотри данные в таблице, 1–2 столбцы):
 = 700/10 = 70,
= 700/10 = 70, 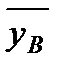 = 230/10 = 23.
= 230/10 = 23.
Выполнив все вычисления в таблице (3 – 7 столбцы), получаем:
Σ(xi–  )(yi–
)(yi– 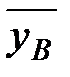 ) =1520,
) =1520,
Σ(xi–  )2 = 8250,
)2 = 8250,
Σ(yi– 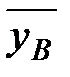 )2 = 298.
)2 = 298.
Подставляя эти значения в соответствующую формулу, вычислим коэффициент корреляции:

| xi | yi | xi– 
| (xi–  )2 )2
| yi– 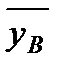
| (yi– 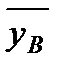 )2 )2
| (xi–  )(yi– )(yi– 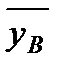 ) )
|
| –45 –35 –25 –15 –5 | –9 –5 –4 –3 | |||||
Таким образом, у выбранных сосен имеет место очень сильная корреляция между общей длиной ствола и длиной его части без ветвей.
Найдем теперь выборочное уравнение прямой регрессии Y на X.
 ,
,
где  ,
,  .
.
Тогда σy/σx= 
Подставляя в выборочное уравнение прямой регрессии Y на X: =70,
=23, rB=0,97, σy/σx=0,19, получим y–23=0,97∙0,19∙(x–70) или y–23=0,18x–12,6.
Окончательно, y=0,18x + 10,4 – искомое уравнение прямой регрессии Y на X.
Задачи контрольной работы для студентов заочной формы обучения
Группа
01. Старшине роты необходимо составить список из 9 солдат в любом порядке. Сколько различных списков он может составить?
|
|
|
02. Сколькими способами можно переставить буквы в слове АРБУЗ?
03. Сколькими способами можно выбрать две монеты из трех: 1,2,3 копейки?
04. Сколько различных 4-х буквенных сочетаний можно составить из слова КАНДЕЛЯБР?
05. В разрезной азбуке было составлено слово КНИГА. Мальчик случайно уронил эти буквы. Сколькими способами он может их составить?
06. Из группы в 20 голов крупного рогатого скота, предназначенного для откорма, для контрольного определения среднесуточного привеса отбирается группа из 8 животных. Сколькими способами это можно сделать?
07. Из 30-ти человек староста группы должен отобрать 10 человек для уборки свеклы в колхозе. Сколько различных списков он может составить?
08. В ящике 20 шаров, среди которых 12 белых, а остальные – голубые. Отбирают наугад 2 шара. Сколько существует вариантов того, что они белые?
09. В урне 16 шаров, среди которых 9 белых, остальные – красные. Отбирают наугад 3 шара. Сколько вариантов того, что два из них окажутся красными?
10. На фабрике по пошиву флагов имеются следующие цвета ткани: красный, белый, голубой, синий, желтый. Сколько можно сшить 3-х цветных флагов с горизонтальными полосами при условии, что одинаковых быть не должно?
Группа
11. В коробке имеется 45 карандашей, 10 из которых сломаны. Художник наудачу извлекает 5 карандашей. Найти вероятность того, что извлеченные карандаши сломаны.
12. Кафедра физвоспитания приобрела для футбольной команды 16 футболок с номерами от 1 до 16. Игроки наудачу берут 10 футболок. Найти вероятность того, что футболка под номером 13 окажется не взятой.
13. Брошены 3 игральные кости. Найти вероятность того, что сумма выпавших очков равна 12, если их произведение равно 48.
14. В читальном зале на полке стоят 37 книг, одна из которых по цитологии. Библиотекарь наудачу берет 8 книг. Найти вероятность того, что среди них нет книги по цитологии.
15. В аудитории находится 40 студентов, 25 из которых не выполнили домашнее задание. Преподаватель наудачу берет тетради у 10 студентов. Найти вероятность того, что все тетради окажутся с выполненным заданием.
16. В магазине имеется 16 плиток шоколада, 12 из которых фабрики «Бабаевский». Покупатель купил три плитки шоколада. Все шоколадки стоят одинаково. Найти вероятность того, что он не купил ни одной шоколадки фабрики «Бабаевский».
|
|
|
17. На грядке посажено 25 кустов средне- и раннеспелого картофеля, из которых 16 раннеспелого сорта. Весь картофель посажен вперемешку. В первый день уборки картофеля выкопано 12 кустов картофеля. Найти вероятность того, что среднеспелого и раннеспелого картофеля выкопано одинаково.
18. Грибник собрал 12 трубчатых и 16 пластинчатых грибов. По дороге домой он уронил три гриба. Найти вероятность того, что он потерял трубчатые грибы.
19. В кодовом замке 10 кнопок с цифрами от 0 до 9. Чтобы его открыть, надо нажать одновременно 3 кнопки. Хозяин, возвращаясь домой, забыл одну цифру в коде замка и стал нажимать третью кнопку наугад. Найти вероятность того, что он откроет замок с первого раза.
20. В парке 15 деревьев. В одном дереве есть дупло, в котором живет белка. Трест зеленого хозяйства провел санитарную рубку, в результате которой было срублено 4 дерева. Найти вероятность того, что белка не осталась без дома.
Группа
21. Два стрелка сделали по одному выстрелу по мишени. Известно, что вероятность попадания в мишень для одного из стрелков равна 0,6, а для другого – 0,7. Найти вероятность того, что хотя бы один из стрелков попадет в мишень.
22. Ящик содержит 90 годных и 10 дефектных деталей. Сборщик последовательно достает из ящика 10 деталей. Найти вероятность того, что среди взятых деталей хотя бы одна дефектная.
23. Два охотника сделали по одному выстрелу по зайцу. Известно, что вероятность попадания для одного из них равна 0,6, а для другого – 0,7. Найти вероятность того, что только один из охотников попадет в зайца.
24. Вероятность попадания в мишень при одном выстреле для первого стрелка равна р, а для второго – 0,7. Известно, что вероятность попадания при одном выстреле обоих стрелков равна 0,35. Найти р.
25. Охотник выстрелил 3 раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,8; а после каждого выстрела уменьшается на 0,1. Найти вероятность того, что он попадет хотя бы один раз.
|
|
|
26. В ящике 10 деталей, среди которых 7 окрашенных. Сборщик наудачу достает 3 детали. Найти вероятность того, что среди взятых деталей не более двух окрашенных.
27. Найти вероятность того, что схема будет работать,
| Р2 |
| Р1 |
| Р3 |
| Р4 |
если заданы вероятности работы каждого независимо работающего устройства: р1 = 0,3, р2 = 0,4, р3 = 0,6, р4 = 0,5.
28. Студент успел подготовить к экзамену 20 вопросов из 30. Какова вероятность того, что из 3 наудачу выбранных вопросов студент знает не менее двух.
29. Экзаменационный билет содержит 3 вопроса. Вероятность того, что студент ответит на первый и второй вопросы билета, равна 0,9, на третий – 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого надо ответить на все вопросы.
30. В команде из 12 спортсменов 5 мастеров спорта. По жеребьевке из команды выбирают 3 спортсменов. Какова вероятность того, что среди выбранных спортсменов не более двух мастеров спорта?
Группа
31. В ящик, содержащий 5 шаров, опущен красный шар, после чего наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется красным, если равновозможны все предположения о первоначальном составе шаров (по цвету).
32. В каждой из трех коробок содержится 9 белых и 7 зеленых шаров. Из первой коробки наудачу взят один шар и переложен во вторую коробку, после чего из второй коробки извлечен один шар и переложен в третью коробку. Найти вероятность того, что шар, наудачу извлеченный из третьей коробки, окажется зеленым.
33. В первом ящике содержится 20 шаров, из них 16 белых, а остальные – синие. Во втором ящике 40 шаров, 8 из которых белые, а остальные синие. Из каждой коробки вынимается по одному шару, а затем из них наудачу извлекают один. Найти вероятность того, что взят синий.
34. В коробку, в которой находится два карандаша, положили зеленый карандаш, после чего из нее вынут один карандаш. Найти вероятность того, что извлеченный карандаш окажется зеленым, если равновозможны все предположения о первоначальном составе карандашей (по цвету).
35. В ящике содержится 20 деталей, изготовленных на заводе № 1, 40 деталей – на заводе № 2. Вероятность того, что деталь, изготовленная на заводе № 1, отличного качества равна 0,7; для детали, изготовленной на заводе № 2, равна 0,4. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.
36. Число деталей, изготавливаемых на I,II, III станках относится как 4:3:3. Вероятность того, что деталь, изготовленная на I станке, является бракованной - 0,2; на II – 0,4; на III – 0.3. Наудачу взятая деталь оказалась бракованной. Найти вероятность того, что деталь изготовлена на I станке.
|
|
|
37. В кондитерской продается в среднем 40% шоколадных конфет, 35% – карамельных и 25% мармеладных. Вероятности продажи шоколадных конфет, карамельных и мармеладных – соответственно, равны 0,6; 0,7 и 0,8. Покупатель в кондитерской приобрел конфеты. Найти вероятность того, что он купил мармеладные конфеты.
38. Два принтера печатают одинаковые тексты. Производительность второго принтера в 2 раза больше производительности первого. Первый принтер печатает в среднем 78% листов с текстами отличного качества, а второй 89%. Наудачу взятый лист с текстом оказался отличного качества. Найти вероятность того, что этот лист произведен вторым принтером.
39. В пирамиде 8 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95, для винтовки без оптического прицела эта вероятность равна 0,7. Стрелок поразил мишень из наудачу взятой винтовки. Найти вероятность того, что он стрелял из винтовки с оптическим прицелом.
40. Событие А может появиться при условии появления одного из несовместных событий В1, В2, В3, образующих полную группу событий. Их вероятности равны: Р(В1)=0,3; Р(В2)=0,5; Р(В3)=0,2. Были также найдены условные вероятности события А при появлении событий В1, В2, В3. Они равны соответственно 0,7, 0,8 и 0,6. Событие А произошло. Найти условную вероятность события В1.
Группа
41. Монету бросают 3 раза. Найти вероятность того, что «герб» выпадет не менее одного раза.
42. В роддоме родилось 12 детей. Найти вероятность того, что среди них 7 мальчиков. Вероятность рождения мальчика 0,51.
43. Имеются две одинаковые лунки, по которым случайным образом разбрасываются 6 шариков. Найти вероятность того, что в каждую лунку попадет ровно 3 шара. Вероятности попадания в лунки одинаковы.
44. Отрезок MN разделен точкой F в отношении 2:3. На отрезок брошены 2 точки. Найти вероятность того, что они попадут на большую часть отрезка. Предполагается, что вероятность попадания точки на отрезок, пропорциональна длине отрезка и не зависит от его расположения.
45. Что вероятнее выиграть у равносильного противника: не менее 3-х партий из 4-х или не менее 6-ти партий из 8-ми?
46. Монету бросают 6 раз. Найти вероятность того, что «решка» выпадет не менее 2-х и не более 3-х раз.
47. В семье 4 ребенка. Найти вероятность того, что среди них 1 девочка и 3 мальчика. Вероятность рождения мальчика равна 0,51.
48. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть 6 партий из 8-ми или 7 из 10-ти?
49. Посадили 8 сортовых тюльпанов. Вероятность того, что тюльпан взойдет р = 0,8. Найти вероятность того, что взойдет ровно 5 тюльпанов.
50. Отрезок разделен на 2 равные части. На отрезок наудачу брошено 6 точек. Найти вероятность того, что на каждую из 2-х частей попадет по 3 точки. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.
Группа
51. Вероятность появления события в каждом из 2100 независимых испытаний равна 0,7. Найти вероятность того, что событие появится: а) не менее 1470 и не более 1500 раз; б) не менее 1470 раз; в) не более 1469 раз.
52. Вероятность появления события в каждом из 21 независимых испытаний равна 0,7. Найти вероятность того, что событие появится в большинстве испытаний.
53. Монета брошена 20 раз. Найти вероятность того, что число выпадений «герба» будет заключено между числами 12 и16.
54. Вероятность появления события в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие появится не менее 75 раз?
55. Вероятность появления положительного результата в каждом из n опытов равна 0,9. Сколько нужно произвести опытов, чтобы с вероятностью 0,98 можно было ожидать, что не менее 150 опытов дадут положительный результат?
56. Найти вероятность того, что событие А наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,6.
57. Вероятность попадания в мишень при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
58. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков.
59. Монета брошена 20 раз. Найти вероятность того, что «герб» выпадет ровно 10 раз
60. Монета брошена 40 раз. Найти вероятность того, что «герб» выпадет на 6 раз больше, чем «решка».
Группа
61. Найти математическое ожидание и дисперсию дискретной случайной величины Х, заданной законом распределения:
| X | 0,21 | 0,54 | 0,61 |
| p | 0,1 | 0,5 | 0,4 |
62. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:
| X | 4,3 | 5,1 | 10,6 |
| p | 0,2 | 0,3 | 0,5 |
63. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X, заданной законом распределения:
| X | ||||
| p | 0,05 | 0,1 | 0,2 | 0,65 |
64. Найти среднее квадратическое отклонение случайной величины X, если задан закон распределения:
| X | ||||
| p | 0,3 | 0,2 | 0,2 | 0,3 |
65. Найти дисперсию и математическое ожидание дискретной случайной величины Х, заданной законом распределения:
| Х | ||||
| p | 0,4 | 0,3 | 0,1 | 0,2 |
66. Найти дисперсию дискретной случайной величины X, заданной законом распределения:
| Х | ||||
| p | 0,2 | 0,1 | 0,3 | 0,4 |
67. Найти математическое ожидание числа бракованных изделий в выработке из 5 изделий, если случайная величина Х задана рядом распределения:
| Х | ||||||
| p | 0,2373 | 0,3955 | 0,2637 | 0,0879 | 0,0146 | 0,0010 |
68. Распределения содержания кремния в отливках из чугуна при определенном составе шахты таково:
| Si% | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 |
| p | 0,32 | 0,25 | 0,14 | 0,12 | 0,08 | 0,05 | 0,02 | 0,01 | 0,01 |
Определить математическое ожидание содержания Si в отливах для данного состава шахты.
69. Вычислить дисперсию и среднее квадратическое отклонение содержания Si в отливках из чугуна для распределения, приведенного в задаче 68.
70. Вычислить дисперсию числа бракованных изделий для распределения, приведенного в задаче 67.
Группа
Случайная величина Х задана интегральной функцией распределения F(x). Найти: 1) дифференциальную функцию распределения f(x); 2) математическое ожидание M(Х); 3) дисперсию D(Х); 4) среднеквадратическое отклонение σ(Х); 5) построить графики функций F(x), f(x).
71. 
| 72. 
|
73. 
| 74. 
|
75. 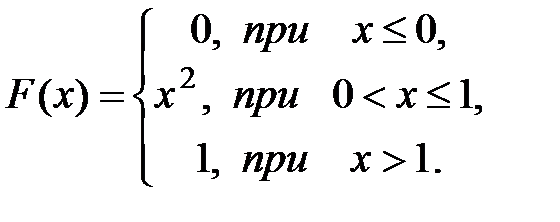
| 76. 
|
77. 
| 78. 
|
79. 
| 80. 
|
Группа
81. Найти M(x) и D(x) равномерно распределенной случайной величины Х, заданной плотностью f(x):

82. Найти M(x) и D(x) равномерно распределенной случайной величины Х, заданной плотностью f(x):

83. Найти M(x) и D(x) равномерно распределенной случайной величины Х, заданной плотностью f(x):
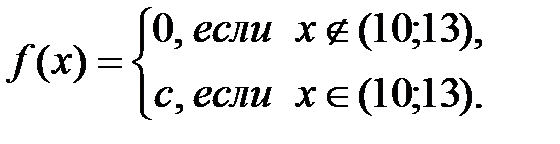
84. Найти M(x) и D(x) равномерно распределенной случайной величины Х, заданной плотностью f(x):

85. Найти M(x) и D(x) равномерно распределенной случайной величины Х, заданной плотностью f(x):

86. Математическое ожидание нормально распределенной случайной величины Х равно 5 и среднее квадратическое отклонение равно 4. Найти плотность вероятностей случайной величины Х.
87. Известно, что случайная величина Х подчинена нормальному закону распределения, M(Х)=4, σ2=25. Найдите плотность вероятностей случайной величины Х.
88. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 8 и 1. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (10;12).
89. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 15 и 5. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (10;15).
90. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 и 14. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (8;12).
Группа
Выборка задана в виде распределения частот. а) Найти распределение
относительных частот. б) Найти эмпирическую функцию по данному распределению выборки и построить график функции F(x).
91.
| 92.
| ||||||||||||||||||
93.
| 94.
| ||||||||||||||||||
95.
| 96.
| ||||||||||||||||||
97.
| 98.
| ||||||||||||||||||
99.
| 100.
|
Группа
101. Построить полигон частот по данному распределению выборки:
| xi | ||||
| ni |
102. Построить полигон относительных частот по данному распределению выборки:
| xi | |||||
| wi | 0,1 | 0,2 | 0,1 | 0,25 | 0,35 |
103. Построить полигон частот по данному распределению выборки:
| xi | |||||
| ni |
104. Построить полигон относительных частот по данному распределению выборки:
| xi | |||||
| wi | 0,15 | 0,2 | 0,25 | 0,3 | 0,1 |
105. Построить полигон частот по данному распределению выборки:
| xi | ||||
| ni |
106. Построить гистограмму частот по данному распределению выборки:
| Частичный интервал | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 |
| Сумма частот вариант интервала ni |
107. Построить гистограмму частот по данному распределению выборки:
| Частичный интервал | 5 – 10 | 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 |
| Сумма частот вариант интервала, ni |
108. Построить гистограмму относительных частот по данному распределению:
| Частичный интервал | 2 – 5 | 5 – 8 | 8 – 11 | 11 – 14 | 14 – 17 |
| Сумма относительных частот вариант интервала, wi | 0,18 | 0,06 | 0,16 | 0,2 | 0,4 |
109. Построить гистограмму относительных частот по данному распределению:
| Частичный интервал | 0 – 5 | 5 – 10 | 10 – 15 |
| Сумма относительных частот вариант интервала, wi | 0,3 | 0,5 | 0,2 |
110. Построить гистограмму относительных частот по данному распределению:
| Частичный интервал | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 | 10 – 12 |
| Сумма относительных частот вариант интервала, wi | 0,1 | 0,25 | 0,45 | 0,15 | 0,05 |
Группа
111. Из генеральной совокупности извлечена выборка объема n=40:
| xi | ||||
| ni |
Найти несмещенную оценку генеральной средней.
112. Найти выборочную среднюю по данному распределению выборки объема n=15:
| xi | |||
| ni |
113. По выборке объема n=81 найдена смещенная оценка DВ=5 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.
114. В итоге пяти измерений (без систематических ошибок) длины бруска одним прибором получены следующие результаты: 804, 806, 807, 809, 810. Найти: а) выборочную среднюю длину бруска; б)выборочную и исправленную дисперсии ошибок прибора.
115. Найти выборочную дисперсию по данному распределению выборки объема n = 27:
| xi | |||
| ni |
116. Найти выборочную дисперсию по данному распределению выборки объема n = 120:
| xi | ||||
| ni |
117. Найти выборочную дисперсию по данному распределению выборки объема n = 75:
| xi | 34,7 | 35,4 | 35,9 | 36,3 |
| ni |
118. Найти выборочную дисперсию по данному распределению выборки объема n = 20:
| xi | 0,004 | 0,005 | 0,008 |
| ni |
119. Найти выборочную дисперсию по данному распределению выборки объема n = 34:
| xi | |||
| ni |
120. Найти выборочную дисперсию по данному распределению выборки объема n = 44:
| xi | 0,3 | 0,7 | 0,9 |
| ni |
Группа
121. Из генеральной совокупности извлечена выборка объема n = 10:
| xi | ||||||
| ni |
Оценить с надежностью 0,99 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
122. Из генеральной совокупности извлечена выборка объема n=10:
| xi | ||||
| ni |
Оценить с надежностью 0,95 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
123. Из генеральной совокупности извлечена выборка объема n = 11:
| xi | |||||
| ni |
Оценить с надежностью 0,95 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.
124. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 20 найдена выборочная средняя  = 15 и «исправленное» среднее квадратическое отклонение s = 2. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,99.
= 15 и «исправленное» среднее квадратическое отклонение s = 2. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,99.
125. Даны «исправленное» среднее квадратическое отклонение s = 0,5; выборочная средняя  = 3;
= 3;  = 2,20. Найти доверительный интервал для оценки неизвестного математического ожидания, нормально распределенной случайной величины X.
= 2,20. Найти доверительный интервал для оценки неизвестного математического ожидания, нормально распределенной случайной величины X.
126. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением σ =8. Найти доверительный интервал для оценки неизвестного математического ожидания, если выборочная средняя  = 16,6, объем выборки n = 25 и заданная надежность γ=0,95.
= 16,6, объем выборки n = 25 и заданная надежность γ=0,95.
127. Даны среднее квадратическое отклонение σ = 10, выборочная средняя  = 7,8 и объем выборки нормально распределенного признака n = 10.
= 7,8 и объем выборки нормально распределенного признака n = 10.
Найти доверительный интервал для оценки неизвестного математического ожидания с заданной надежностью γ=0,95.
128. Количественный признак Х генеральной совокупности распределили нормально. По выборке объема n = 40 найдено «исправленное» среднее квадратическое отклонение s = 0,8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,999.
129. Количественный признак Х генеральной совокупности распределили нормально. По выборке объема n=10 найдено «исправленное» среднее квадратическое отклонение s=5. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,99.
130. По данным выборки объема n=19 из генеральной совокупности нормально распределенного количественного признака найдено «исправленное» среднее квадратическое отклонение s = 5,4. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,95.
Группа
Вычислить выборочный коэффициент корреляции и найти выборочное уравнение прямой регрессии Y на X.
131.
| X | ||||||||||
| Y |
132.
| X | ||||||||||
| Y |
133.
| X | ||||||||||
| Y |
133.
| X | ||||||||||
| Y |
135.
| X | ||||||||||
| Y |
136.
| X | ||||||||||
| Y |
137.
| X | ||||||||||
| Y |
138.
| X | ||||||||||
| Y |
139.
| X | ||||||||||
| Y |
140.
| X | ||||||||||
| Y |
Группа
Найти основные выборочные характеристики  , s2, s, V, sx; с надежностью 95% указать доверительный интервал для оценки генеральной средней xГ для следующей выборки:
, s2, s, V, sx; с надежностью 95% указать доверительный интервал для оценки генеральной средней xГ для следующей выборки:
| Номер задачи | ||||||||||||
| 141. | 142. | 143. | 144. | 145. | 146. | 147. | 148. | 149. | 150. | |||
| 40,8 26,4 33,2 29,5 36,1 32,8 33,5 36,4 37,1 39,6 41,0 28,3 30,6 37,9 39,2 32,5 35,6 34,8 36,9 34,2 | 12,6 18,7 15,3 14,8 19,5 13,7 16,4 15,2 16,3 12,9 18,5 16,5 15,4 13,6 16,9 15,8 17,3 19,6 15,8 19,6 | 19,7 20,3 25,6 24,3 28,9 29,6 19,4 23,5 25,8 29,4 28,2 26,1 23,9 25,8 23,9 26,9 27,6 25,9 24,7 28,5 | 18,6 19,5 23,8 15,4 39,7 24,5 19,8 20,5 26,5 23,4 21,6 29,7 29,7 24,6 19,4 16,5 16,8 14,4 13,8 22,4 | 26,5 18,4 29,4 35,8 26,9 34,2 26,7 34,6 35,1 32,8 30,9 28,7 29,6 31,5 36,4 34,8 39,5 32,9 34,4 30,4 | 29,8 30,5 31,6 29,6 35,7 36,8 29,4 21,6 29,7 24,6 34,8 36,4 32,1 39,7 34,5 34,8 31,5 34,8 37,9 29,6 | 45,8 50,4 48,4 53,2 49,5 52,6 48,7 51,9 45,9 46,8 49,5 51,2 46,3 48,7 48,9 48,3 47,6 48,3 49,5 48,6 | 95,4 82,5 86,9 90,2 89,1 85,6 87,5 86,4 89,3 92,1 90,3 86,9 87,4 90,4 94,6 93,2 87,5 86,4 93,4 86,5 | 32,5
35,4
18,9
21,5
26,5
23,0
26,1
28,4
19,8
31,5
30,6
25,8
31,0
36,4
26,5
28,7
23,4
26,8
29
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

