 |
Задания для самостоятельной работы
|
|
|
|
1. Двухмесячные объёмы продаж продукции некоторого предприятия удовлетворительно описываются двумерным случайным вектором с плотностью распределения вероятности

Найти:
a) константу с;
b) функцию распределения F(x,y);
c) исследовать случайные величины X и Y на независимость.
Тема 11. Понятие о различных формах закона больших чисел.
Вопросы для самопроверки
1. Какие утверждения принято называть «законом больших чисел»?
2. Сформулируйте центральную предельную теорему Лапласа.
3. Сформулируйте теорему, известную как «неравенство Чебышева».
Тема 12. Математическая статистика. Основные понятия и определения.
Вопросы для самопроверки
1. Какие задачи рассматриваются в математической статистике?
2. Что такое генеральная совокупность?
3. Что называется выборкой из генеральной совокупности?
4. Какое различие между выборкой и вариационным рядом?
5. Опишите понятия: полигон частот, полигон относительных частот, гистограмма.
6. Что такое теоретическая и эмпирическая функции распределения?
7. Как построить эмпирическую функцию распределения?
8. Как находятся выборочное среднее и выборочная дисперсия?
Задания для самостоятельной работы
1. По выборке:

| ||||||

|
найти выборочное среднее, выборочную дисперсию, исправленную дисперсию, выборочное среднее квадратическое отклонение, исправленное среднее квадратическое отклонение.
Тема 13. Классификация оценок. Точечное и интервальное оценивание параметров.
Вопросы для самопроверки
1. Какая оценка неизвестного параметра теоретического распределения называется состоятельной? Приведите пример состоятельной оценки.
|
|
|
2. Какая оценка неизвестного параметра теоретического распределения называется несмещенной?
3. Что значит, что оценка является эффективной?
4. Что является критерием состоятельности оценки?
5. Как доказать, что оценка является несмещенной?
6. Как находятся точечные оценки математического ожидания и дисперсии?
7. Являются точечные оценки математического ожидания и дисперсии состоятельными и несмещенными?
8. Что такое доверительный интервал?
9. Что такое доверительная вероятность?
10. Как строится доверительный интервал для математического ожидания?
Тема 14. Проверка статистических гипотез.
Вопросы для самопроверки
1. Что такое «статистическая гипотеза»?
2. Какую гипотезу называют нулевой, какую – конкурирующей?
3. Какие ошибки относят к ошибкам первого рода, какие – второго рода?
4. Что такое статистический критерий?
5. В каком случае гипотеза принимается, в каком – отвергается?
6. Что такое «критерий согласия»?
7. Какая случайная величина рассматривается в качестве критерия при проверке гипотезы о распределении генеральной совокупности?
Варианты индивидуальных заданий для студентов очного отделения
Вариант 1.
1. Из слова НАУГАД выбирается наугад одна буква. Какова вероятность того, что это буква: а) А; б) У?
2. В партии х изделий 1 сорта и десять изделий 2 сорта. Найти х, если вероятность того, что два взятые наугад изделия являются изделиями 1 сорта, равна 6/91.
3. Партия содержит изделия трех категорий: бракованные (шесть штук), стандартные (одна штука), повышенного качества (две штуки). Наугад взято три изделия. Требуется найти вероятность того, что среди взятых либо нет брака, либо число бракованных меньше, чем не бракованных.
4. В урне 4 белых и 2 черных шара. Из этой урны наудачу извлечены 2 шара. Какова вероятность того, что эти шары разного цвета?
|
|
|
5. Два стрелка сделали по одному выстрелу по мишени. Известно, что вероятность попадания в мишень для одного из стрелков равна 0,7, а для другого - 0,8. Найдите вероятность того, что только один из стрелков попадет в мишень!
6. В тире имеются шесть ружей, вероятности попадания из которых равны соответственно 0,3; 0,4; 0,5; 0,6; 0,7; 0,8. Определить вероятность попадания при одном выстреле, если стреляющий берет одно из ружей наудачу.
7. В студенческом стройотряде две бригады первокурсников и одна второкурсников. В каждой бригаде первокурсников 5 юношей и 3 девушки, а в бригаде второкурсников 4 юноши и 4 девушки. По жеребьевке из отряда выбрали одну из бригад и из нее одного человека для поездки в город. Выбранный человек оказался юношей. Какова вероятность, что он первокурсник?
8. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0,005. Телефонная станция обслуживает 600 абонентов. Какова вероятность того, что в течение часа позвонят пять абонентов?
9. Найдите наиболее вероятное число выпадений шестерки при подбрасываниях игральной кости.
10. По мишени производится 4 независимых выстрела с вероятностью попадания при каждом выстреле Р=0,8. Требуется:
а) найти закон распределения дискретной случайной величины X, равной числу попаданий в мишень;
б) найти вероятность события: 1  X
X  3
3
в) построить многоугольник распределения;
г) найти математическое ожидание и дисперсию случайной величины X.
11. Случайная величина X задана функцией распределения:

а) убедитесь, что величина X имеет плотность вероятности, и найдите ее;
б) найдите вероятность события;
в) найдите математическое ожидание и дисперсию.
Вариант 2.
1. На шести карточках написаны буквы В, Д, 3, О, У, X. После тщательного перемешивания наугад вынимают одну карточку за другой и раскладывают их в том порядке, в каком они были вынуты. Найти вероятность того, что на карточках будет написано слово "ВОЗДУХ".
2. Партия состоит из изделий 1 и 2 сорта. Если из этой партии взять наугад два изделия, то вероятность того, что оба изделия 1 сорта, равна 15/26, а вероятность того, что взятые изделия разных сортов, равна 5/13. Найти число изделий в партии.
3. В урне 6 белых и 4 черных шара. Из этой урны наудачу извлекли 5 шаров. Какова вероятность, что 2 из них белые, а 3 черные?
|
|
|
4. Партия содержит изделия трех категорий: бракованные (шесть штук), стандартные (одна штука), повышенного качества (две штуки). Найти вероятность того, что среди двух наугад взятых изделий нет брака.
5. Два стрелка сделали по одному выстрелу по мишени. Известно, что вероятность попадания в мишень для одного из стрелков равна 0.6, а для другого - 0.7. Найдите вероятность того, что хотя бы один из стрелков попадет в мишень.
6. Приборы одного наименования изготавливаются тремя заводами. Первый завод поставляет 45% всех изделий, поступающих на производство, второй -30% и третий - 25%. Вероятность безотказной работы прибора, изготовленного первым заводом, равна 0,8, вторым - 0,85 и третьим - 0,9. Определить вероятность безотказной работы прибора, поступившего на производство.
7. 35% приборов собирает специалист высокой квалификации и 65 % - средней. Надежность работы прибора, собранного специалистом высокой квалификации равна 0,95; надежность прибора, собранного специалистом средней квалификации равна 0,75. Наудачу взятый прибор оказался надежным. Определить вероятность того, что он собран специалистом средней квалификации.
8. Завод выпускает в среднем 99,8% доброкачественных и 0,2% бракованных изделий. Какова вероятность того, что среди наудачу взятых 500 изделий число бракованных будет больше трех?
9. Контрольное задание состоит из 10 вопросов, предусматривающих ответы "да" и "нет". Найдите наиболее вероятное число правильных ответов, которые даст учащийся, если он станет выбирать ответ по каждому вопросу наудачу.
10. В урне 7 шаров, из которых 4 белых, а остальные черные. Из этой урны наудачу извлекаются 3 шара; Х- число извлеченных белых шаров.
а) Найдите закон распределения дискретной случайной величины X:
б) найдите вероятность события Х≤ 2;
в) постройте многоугольник распределения;
г) найдите математическое ожидание и дисперсию случайной величины X.
11. Дана функция

а) При каком значении коэффициента а функция f(x) является плотностью вероятности некоторой случайной величины X?
|
|
|
б) Найдите функцию распределения F(x);
в) Вычислите вероятность попадания случайной величины X в промежуток (ОД);
г) найдите математическое ожидание и дисперсию случайной величины X
Вариант 3.
1. 25 экзаменационных билетов содержат по два вопроса, которые не повторяются. Экзаменующийся может ответить только на 45 вопросов. Какова вероятность того, что вытянутый билет состоит из подготовленных им вопросов?
2. В партии из 20 запасных резисторов имеется четыре нестандартных. Для проверки наудачу выбирают семь резисторов из этой партии. Определить вероятность того, что среди них окажутся ровно два нестандартных.
3. Какова вероятность того, что в написанном наудачу трехзначном числе 2 цифры одинаковы, а третья отличается от них?
4. Партия содержит изделия трех категорий: бракованные (шесть штук), стандартные (одна штука), повышенного качества (две штуки). Наугад берут два изделия. Найти вероятность того, что взятые изделия одной категории.
5. 2 стрелка сделали по одному выстрелу по мишени. Известно, что вероятность попадания в мишень для одного из стрелков равна 0,65, а для другого - 0,7. Найдите вероятность того, что оба стрелка попадут в цель.
6. Брак в продукции завода вследствие дефекта А составляет 5%, причем среди забракованной по признаку А продукции в 6% случаев встречается дефект В, а в продукции, свободной от дефекта А, дефект В встречается в 2% случаев. Найти вероятность встретить дефект В во всей продукции.
7. На некоторой фабрике машина А производит 40% всей продукции, а машина В - 60%. В среднем 9 единиц из 1000 единиц продукции, произведенных машиной А, оказывается браком, а у машины В - брак 2 единицы из 500. Некоторая единица продукции, выбранная случайным образом из дневной продукции, оказалась браком. Какова вероятность того, что она произведена на машине В?
8. Охотники делают шесть выстрелов по цели, вероятность попадания при каждом выстреле равна 0,7. Для поражения цели достаточно двух попаданий. Найти вероятность того, что цель будет поражена.
9. Вероятность изготовления стандартной детали 0,95. Сколько деталей должно быть в партии, чтобы наиболее вероятное число нестандартных деталей в ней равнялось 55?
10. Дискретная случайная величина X - число мальчиков в семьях с пятью детьми. Предполагая равновероятными рождение мальчика и девочки,
а) найдите закон распределения X;
б) постройте многоугольник распределения;
в) найдите вероятность события А - в семье не менее 2, но не более 3 мальчиков;
г) найдите математическое ожидание и дисперсию случайной величины X.
|
|
|
11. Случайная величина X задана функцией распределения F(x).

а) Убедитесь, что она имеет плотность вероятности и найдите ее;
б) Вычислите вероятность попадания случайной величины X в промежуток (-1; 1);
в) Найдите математическое ожидание и дисперсию случайной величины Х.
Вариант 4.
1. Бросают игральную кость. Какова вероятность выпадения номера, большего 4?
2. В ящике содержится десять одинаковых деталей, помеченных номерами 1, 2,..., 10. Наугад извлечены шесть деталей. Какова вероятность того, что среди извлеченных деталей окажутся:
а) деталь № 1?
б) деталь № 1 и деталь № 2?
3. В некоторый день недели во всех классах школы должно быть по 6 уроков. В этот день случайным образом ставятся в расписание 3 урока одного учителя и 2 урока другого. Какова вероятность того, что эти учителя не будут одновременно заняты?
4. В ящике пять деталей 1 сорта и десять деталей 2 сорта. Из ящика наугад берут пять деталей. Найти вероятность того, что среди отобранных деталей есть хотя бы три 2 сорта.
5. Два стрелка сделали по одному выстрелу по мишени. Известно, что вероятность попадания в мишень для одного из стрелков равна 0,8, а для другого – 0,75. Найдите вероятность того, что ни один из стрелков не попадет в цель.
6. На позиции может случайно и равновероятно оказаться один из пяти стрелков. Три из них вооружены оружием с оптическим прицелом, два - без оптического. Вероятность поражения цели из оружия с оптическим прицелом равна 0,95, без оптического - 0,7. Определить вероятность того, что при произведении одного выстрела случайно оказавшимся на позиции стрелком цель будет поражена.
7. Из 20 студентов, пришедших на экзамен, 8 подготовлены отлично, 6 - хорошо, 4 - посредственно и 2 - плохо. В экзаменационных билетах имеется 40 вопросов. Студент, подготовленный отлично, знает все вопросы, хорошо - 35, посредственно - 25 и плохо - 10 вопросов. Некий студент ответил на все 3 вопроса билета. Найдите вероятность того, что он подготовлен плохо.
8. Группа из пяти охотников участвует в охоте на медведя, причем каждый из них делает по одному выстрелу. Вероятность попадания в медведя при одном выстреле 1/3. Чтобы убить медведя, требуется не менее трех попаданий. Найти вероятность того, что медведь будет убит.
9. Вероятность того, что денежный приемник автомата при опускании монеты сработает неправильно, равна 0,03. Найдите наиболее вероятное число случаев правильной работы автомата, если будет опущено 150 монет.
10. С вероятностью попадания при одном выстреле 0,7 охотник стреляет по дичи до первого попадания, но успевает сделать не более 4 выстрелов. Дискретная величина X - число промахов.
а) Найдите закон распределения X;
б) найдите вероятность события: 1  Х
Х  3;
3;
в) постройте многоугольник распределения;
г) найдите математическое ожидание и дисперсию X.
11. Случайная величина X задана функцией распределения:

а) Убедитесь, что она имеет плотность вероятности, и найдите ее;
б) найдите вероятность события 1 <Х< 3;
в) найдите математическое ожидание и дисперсию X.
Вариант 5
1. Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность того, что получится слово ДВА?
2. Партия содержит изделия трех категорий: бракованные (одна штука), стандартные (семь штук), повышенного качества (семь штук). Наугад берут три из них. Требуется найти вероятность того, что остаток партии будет содержать изделия двух категорий поровну.
3. В группе из 10 человек 6 мужчин и 4 женщины. Случайным образом выбирают по очереди двоих. Какова вероятность того, что эти двое одного пола?
4. В партии 11 изделий, из них четыре нестандартных. Наугад берут четыре изделия. Найти вероятность того, что среди взятых изделий больше стандартных, чем нестандартных.
5. Два стрелка сделали по одному выстрелу по мишени. Известно, что вероятность попадания в мишень для одного из стрелков равна 0,9, а для другого - 0,85. Найдите вероятность того, что хотя бы один из стрелков не попадет в мишень.
6. В вычислительной лаборатории имеются шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на машине, выбранной наудачу. Найти вероятность того, что до окончания расчета машина не выйдет из строя.
7. Из 18 стрелков 5 попадает в мишень с вероятностью 0,6: 7 – с вероятностью 0,7; 4 - с вероятностью 0,6 и 2 - с вероятностью 0,5. Наудачу выбранный стрелок не попал в мишень. К какой группе вероятнее всего принадлежит стрелок?
8. Вероятность попадания в цель при одном выстреле равна 0,7. Найти вероятность того, что при 20 независимых выстрелах цель будет поражена не более 14 раз.
9. Вероятность того, что денежный приемник автомата при опускании одной монеты сработает правильно, равна 0,97. Сколько нужно опустить монет, чтобы наивероятнейшее число случаев правильной работы автомата было равно 100?
10. Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка при одном выстреле - 0,5, для второго 0,4. Дискретная случайная величина Х- число попаданий в мишень. Требуется:
а) найти закон распределения X;
б) построить многоугольник распределения;
в) найти вероятность события X  1
1
г) найти математическое ожидание и дисперсию X.
11. Случайная величина X задана функцией плотности вероятности

Найдите:
а) постоянную C;
б) функцию распределения F(x);
в) вероятность события 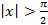
г) математическое ожидание и дисперсию
Вариант 6
1. В барабане револьвера семь гнезд, из них в четыре заложены боевые патроны, а остальные оставлены пустыми. Барабан приводится во вращение, в результате чего против ствола случайным образом оказывается одно из гнезд. После этого нажимается спусковой крючок. Найти вероятность того, что, повторив такой опыт дважды, мы оба раза произведем выстрел.
2. Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что это число кратно 5?
3. В урне 10 шаров, из которых 2 белых, 3 черных и 5 синих. Наудачу извлечены 3 шара. Какова вероятность того, что все 3 шара разного цвета?
4. В первом ящике 30 % деталей первого сорта, а во втором - 40 %. Вынимают по одной детали из каждого ящика. Определить вероятность того, что обе вынутые детали первого сорта.
5. Вероятность попадания в мишень при одном выстреле для первого стрелка равна р, а для второго – 0,7, Известно, что вероятность ровно одного попадания при одном выстреле обоих стрелков равна 0,38. Найдите р.
6. Радиолампа может принадлежать к одной из трех партий с вероятностями  =
=  =0,25; Р3 — 0,5. Вероятности того, что лампа проработает заданное число часов, равны соответственно 0,1; 0,4; 0,2. Определить вероятность того, что лампа проработает заданное число часов.
=0,25; Р3 — 0,5. Вероятности того, что лампа проработает заданное число часов, равны соответственно 0,1; 0,4; 0,2. Определить вероятность того, что лампа проработает заданное число часов.
7. Для сдачи экзамена студентам было необходимо подготовить 30 вопросов. Из 25 студентов 10 подготовили все вопросы, 8-25 вопросов, 5-20 вопросов и 2-15 вопросов. Вызванный студент ответил на поставленный вопрос. Найдите вероятность того, что этот студент подготовил только половину вопросов.
8. Есть 5 одинаковых партий изделий. Каждая партия состоит из двух изделий первого сорта и трех изделий второго сорта. Из каждой партии наугад берут по изделию. Найти вероятность того, что среди выбранных ровно три изделия одного сорта.
9. Производится 10 независимых выстрелов по цели, вероятность попадания в которую при одном выстреле равна 0,2. Найдите наиболее вероятное число попаданий.
10. В коробке имеются 7 карандашей, из которых 4 красные. Из этой коробки наудачу извлекаются 3 карандаша. Требуется:
а) найти закон распределения случайной величины X, равной числу красных карандашей в выборке;
б) построить многоугольник распределения;
в) найти вероятность события 0 < Х  2;
2;
г) найти математическое ожидание и дисперсию.
11. Случайная величина X задана функцией распределения:
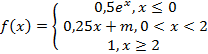
Найдите:
число т и функцию плотности вероятности  ;
;
вероятность события 1 <Х< 4;
математическое ожидание и дисперсию случайной величины X.
Вариант 7.
1. Наугад указываются месяц и число некоторого невисокосного года. Какова вероятность того, что это будет воскресенье, если всего в этом году 53 воскресенья, а соответствие чисел дням недели неизвестно?
2. Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что это число окажется делителем 20?
3. Числа 3, 5, 6, 9, 11, 17, 18 написаны на одинаковых карточках. Две карточки берутся наугад. Какова вероятность того, что образованную из двух полученных чисел дробь можно сократить?
4. Партия состоит из 18 деталей 1 сорта и 12 деталей 2 сорта. Из партии наугад берут две детали. Найти вероятность того, что отобранные детали одного сорта.
5. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,2. Произведено три независимых измерения. Найдите вероятность того, что не более чем в одном измерении допущенная ошибка превысит заданную точность.
6. Среди 350 механизмов 160 первого сорта, 110 - второго сорта и 80 – третьего сорта. Вероятность брака среди механизмов первого сорта равна 0,01, среди механизмов второго сорта - 0,02, среди механизмов третьего сорта - 0,04. Взятый механизм оказался исправным. Найти вероятность того, что он второго сорта.
7. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих шаров наудачу взят один шар. Найдите вероятность того, что шар - белый.
8. Вероятность брака при производстве деталей р=0,02. Найти вероятность того, что в партии из 400 деталей окажутся бракованными от 7 до 10 деталей.
9. Рабочий обслуживает 12 станков одного типа. Вероятность того, что станок потребует внимания рабочего в течение часа, равна 1/3. Найдите вероятность того, что в течение часа 4 станка потребуют внимания рабочего.
10. Из 25 контрольных работ, среди которых 5 оценены на «отлично», наугад извлекают 3 работы. Требуется:
а) найти закон распределения случайной величины X, равной числу оцененных на "отлично" работ среди извлеченных;
б) найти, чему равна вероятность события Х> 0;
в) построить многоугольник распределения;
г) найти математическое ожидание и дисперсию.
11. Задана плотность вероятности случайной величины X:

Найдите:
а) коэффициент а;
б) функцию распределения F(x);
в) вероятность события X > 1;
г) математическое ожидание и дисперсию.
Вариант 8.
1. Набирая номер телефона, абонент забыл последние три цифры, помня лишь то, что они различны, и набрал их наудачу. Найти вероятность того, что набран верный номер.
2. Наудачу выбрано двузначное число. Вероятность того, что это число окажется кратным 5?
3. На 10 карточках написаны буквы "а", "а", "а", "м", "м", "т", "т", "е", "и", "к". После перемешивания карточки раскладываются в ряд. Какова вероятность того, что получится слово "математика"?
4. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа не потребует внимания рабочего первый станок, равна 0,9; второй - 0,8; третий - 0,85. Найти вероятность того, что в течение часа хотя бы один станок потребует внимания рабочего.
5. В ящике 10 деталей, среди которых 7 окрашенных. Сборщик наудачу достает 4 детали. Найдите вероятность того, что все детали окрашенные.
6. Имеются две партии деталей, причем известно, что в одной партии все детали удовлетворяют техническим условиям, а в другой партии 25% деталей - недоброкачественные. Деталь, взятая из наудачу выбранной партии, оказалась доброкачественной. Определись вероятность того, что вторая деталь из этой же партии окажется доброкачественной, если первая деталь после проверки возвращена в партию.
7. 60% учащихся в школе - девочки. 80% девочек и 75% мальчиков имеют билеты в театр. В учительскую принесли кем-то потерянный билет. Какова вероятность того, что этот билет принадлежал девочке?
8. Вероятность поражения цели при одном выстреле равна 0,2. Найти вероятность того, что при трех выстрелах цель будет поражена один раз.
9. Вероятность появления события А в каждом из 1500 независимых испытаний равна 0,4. Найдите вероятность того, что число появлений события А заключено между 570 и 630.
10. Имеется 5 ключей, из которых только один подходит к замку. Требуется:
а) найти закон распределения случайной величины X, равной числу проб при открывании замка, если испробованный ключ в последующих испытаниях не участвует;
б) найти вероятность события Х> 2;
в) построить многоугольник распределения;
г) найти математическое ожидание и дисперсию случайной величины X.
11. Случайная величина X задана функцией распределения

Требуется:
а) найти число b;
б) найти вероятность события -1 <Х< 2;
в) найти математическое ожидание и дисперсию X.
Вариант 9.
1. В урне 3 белых и 7 черных шаров. Какова вероятность того, что вынутые наугад два шара окажутся черными?
2. Наудачу выбрана кость домино из полного набора. Какова вероятность того, что сумма очков на выбранной кости равна 5?
3. Брошены 3 игральные кости. Какова вероятность того, что на всех костях выпадет четное число?
4. При приемке партии продукции подвергается проверке на выбор половина изделий. Если число бракованных изделий более 2%, то вся партия бракуется (не принимается). Определить вероятность того, что партия из 100 изделий, содержащая 5% брака, будет принята.
5. Вероятность выигрыша по одному билету равна 1/7. Какова вероятность, купив 5 билетов, выиграть по всем пяти?
6. Известно, что 96% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,89 и нестандартную с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.
7. Бросается монета, и если она падает так, что сверху оказывается герб, вынимаем один шар из урны 1; в противном случае - из урны 2. Урна 1 содержит 3 красных и 1 белый шар. Урна 2 содержит 1 красный и 3 белых шара. Какова вероятность того, что вынутый шар - красный?
8. Найти вероятность того, что цель будет поражена не более двух раз при пяти независимых выстрелах, если вероятность поражения цели при одном выстреле равна 0,2.
9. Вероятность появления события А в каждом из независимых испытаний равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,9 можно было ожидать, что событие А появится не менее 75 раз?
10. В партии из 10 деталей имеется 8 стандартных. Из этой партии наудачу взято 4 детали. Требуется:
а) найти закон распределения случайной величины X, равной числу стандартных деталей в выборке;
б) построить многоугольник распределения;
в) найти вероятность события 1 <Х< 3;
г) найти математическое ожидание и дисперсию X.
11. Случайная величина X имеет плотность вероятности

Найдите:
а) число b и функцию распределения F(x);
б) вероятность события 1 <Х< 4;
в) математическое ожидание и дисперсию.
Вариант 10.
1. В партии из 10 резисторов 4 бракованных. Какова вероятность того, что два наугад выбранных резистора окажутся бракованными?
2. Ha одинаковых карточках написаны все целые числа от 1 до 15. Наудачу извлекаются две карточки. Какова вероятность того, что одно выбранное число больше 6, а другое - меньше?
3. Цифры 1, 2, 3, 4 и 5 написаны на карточках и тщательно перемешаны. Случайным образом эти карточки разложены в ряд. Какова вероятность того, что получено четное число?
4. Партия содержит изделия трех категорий: бракованные (одна штука), стандартные (семь штук) и повышенного качества (семь штук). Наугад берут три из них. Требуется найти вероятность того, что среди них нет бракованных, при условии, что лишь одно из них повышенного качества.
5. Вероятность выигрыша по одному билету лотереи равна 1/7. Какова вероятность, купив 5 билетов, выиграть по двум из них?
6. Из 18 стрелков 5 попадают в мишень с вероятностью 0,8; семь – с вероятностью 0,7; четыре - с вероятностью 0,6; два - с вероятностью 0,5. Наудачу выбранный стрелок произвел выстрел, но в мишень не попал. К какой группе вероятнее всего принадлежал этот стрелок?
7. В группе 20 мужчин и 30 женщин. 5% мужчин и 3% женщин дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, Что это мужчина?
8. Производится независимо три выстрела по мишени в тире. Вероятность поражения цели одним выстрелом равна 0,7. Найти вероятность попадания в цель.
9. Вероятность появления положительного результата в каждом из независимых испытаний равна 0,9. Сколько нужно произвести испытаний, чтобы с вероятностью 0,98 можно было ожидать, что не менее 150 испытаний дадут положительный результат?
10. Дважды брошена игральная кость. Случайная величина X равна разности между числом очков при первом и втором бросании. Требуется:
а) найти закон распределения X;
б) найти вероятность события 2 < Х< 4;
в) найти математическое ожидание и дисперсию X;
г) построить многоугольник распределения.
11. Случайная величина X задана функцией распределения

Требуется:
а) проверить, что она имеет плотность вероятности и найти ее;
б) найти вероятность события 2 <Х< 6;
в) найти математическое ожидание и дисперсию X.
Вариант 11.
1. Брошены две игральные кости. Чему равна вероятность того, что абсолютная величина разности выпавших очков равна двум?
2. Какова вероятность того, что в наудачу выбранном двузначном числе цифры одинаковы?
3. В урне 5 белых и 5 черных шаров. Из этой урны последовательно извлечены все шары по одному и разложены в ряд. Какова вероятность того, что цвета шаров чередуются?
4. Партия содержит изделия трех категорий: бракованные (девять штук), стандартные (две штуки), повышенного качества (восемь штук). Найти вероятность того, что все взятые изделия - повышенного качества, если наугад берут три изделия.
5. Пусть всхожесть семян ржи составляет 90 %. Чему равна вероятность того, что из семи посеянных семян взойдет пять?
6. Вероятности попадания при каждом выстреле для трех стрелков равны соответственно 4/5, 3/4, 2/3. При одновременном выстреле всех стрелков имелось два попадания. Определить вероятность того, что промахнулся третий стрелок.
7. В группе из 20 стрелков имеются 4 отличных, 10 хороших и 6 посредственных стрелков. Вероятность попадания в цель при одном выстреле для отличного стрелка равна 0,9, для хорошего - 0,7, для посредственного - 0,5. Найдите вероятность того, что два наудачу выбранных стрелка попадут в цель.
8. Вероятность того, что изделие не выдержит испытания, равна 0,0004. Найти вероятность того, что из 1000 изделий не выдержат испытания не менее двух изделий.
9. По данным технического контроля 2 % изготовленных автоматических станков нуждаются в дополнительной регулировке. Найдите вероятность того, что из 6 изготовленных станков 4 нуждаются в дополнительной регулировке.
10. Игральная кость бросается шесть раз. Случайная величина X равна количеству выпадений шестерки. Требуется:
а) найти закон распределения случайной величины X;
б) найти вероятность события Х  4;
4;
в) построить многоугольник распределения;
г) найти математическое ожидание и дисперсию X.
11. Случайная величина X имеет плотность распределения вероятностей

Найдите:
а) число т и функцию распределения F(x);
б) вероятность события 0 <Х< 5;
в) математическое ожидание и дисперсию X.
Вариант 12.
1. В мастерскую для ремонта поступило 15 телевизоров. Известно, что 6 из них нуждаются в общей регулировке. Мастер берет первые попавшиеся 5 штук. Какова вероятность того, что 2 из них нуждаются в общей регулировке?
2. Три орудия стреляют в цель независимо друг от друга. Вероятность попадания в цель для первого орудия равна 0,6, для второго - 0,7 и для третьего - 0,75. Найти вероятность хотя бы одного попадания в цель, если каждое орудие делает по одному залпу.
3. На тридцати одинаковых жетонах написаны двузначные числа от 11 до 40. Жетоны перемешивают и вынимают один случайным образом. Какова вероятность вынуть жетон с номером, кратным двум или трем?
4. Партия содержит изделия трех категорий: бракованные (девять штук), стандартные (две штуки), повышенного качества (две штуки). Найти вероятность того, что все взятые изделия бракованные, если наугад берут три изделия.
5. Из цифр 1, 2, 3, 4, 5 выбирается одна, а из четырех оставшихся - вторая. Найдите вероятность того, что оба раза будет выбрана нечетная цифра.
6. Два стрелка поочередно стреляют в мишень. Вероятности попадания первыми выстрелами для них равны соответственно 0,4 и 0,5, а вероятности попадания при последующих выстрелах для каждого увеличиваются на 0,05. Какова вероятность, что первым произвел выстрел первый стрелок, если при пятом выстреле произошло попадание в мишень?
7. В каждой из трех урн по 6 черных и 4 белых шара. Из первой урны наудачу извлечен шар и переложен во вторую, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найдите вероятность того, что шар, извлеченный затем из третьей урны, окажется белым.
8. В результате проведения опыта событие А появляется с вероятностью 0,001. Опыт повторяется 2000 раз. Какова вероятность того, что событие А появится не менее двух раз и не более четырех раз?
9. В семье 5 детей. Найдите вероятность того, что среди детей 2 мальчика, если вероятность рождения мальчика равна 0,5.
10. Рабочий обслуживает четыре независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,7, для второго - 0,75, для третьего - 0,8, для четвертого - 0,9. Требуется:
а) найти закон распределения случайной величины X, равной числу станков, которые не потребуют внимания рабочего;
б) найти вероятность события X < 3;
в) найти математическое ожидание и дисперсию X.
11. Случайная величина задана функцией распределения

Требуется:
а) проверить, что она имеет плотность вероятности и найти её;
б) найти вероятность события 0 < X < 3;
в) найти математическое ожидание и дисперсию X.
Вариант 13.
1. У сборщика 12 деталей, мало отличающихся друг от друга. Из них пять - первого вида, четыре - второго и три - третьего. Какова вероятность того, что среди шести взятых одновременно деталей три окажутся первого вида, две - второго, одна - третьего?
2. Наугад выбираются по одной букве из слов "дама" и "мама". Какова вероятность того, что эти буквы одинаковы?
3. В урне десять шаров. Вероятность того, что два извлеченных из нее шара окажутся белыми, равна 2/15. Сколько в урне белых шаров?
4. В цехе работают 20 станков. Из них 10 марки А, 6 марки В и 4 марки С. Вероятность того, что качество детали окажется отличным, для этих станков соответственно равна 0,9; 0,8; 0,7. Какова вероятность того, что наугад взятая деталь окажется отличного качества?
5. Из цифр 1, 2, 3, 4, 5 выбирается одна, а из оставшихся - вторая. Найдите вероятность того, что их сумма будет больше 4.
6. Третья часть одной из трех партий деталей является второсортной, остальные детали во всех партиях первосортные. Деталь, взятая наугад из одной парт
|
|
|


