 |
Перестановка, размещение и сочетание с повторением
|
|
|
|
Размещение с повторением из n элементов по k называется упорядоченная (n,k) – выборка с возможными повторениями элементов.
Пример: Пусть A={1,2,3}
Перечислим все размещения с повторением из элементов множества A по 2: 1,1; 1,2; 1,3; 2,1; 2,2; 2,3; 3,1; 3,2; 3,3.
Формула

Сочетанием с повторениями из n элементов по k называется неупорядоченная (n,k) – выборка с возможными повторениями элементов.
Пусть A={1,2,3}
Перечислим все сочетания с повторениями из элементов множества A по 2: 1,1; 1,2; 1,3; 2,3; 3,3.
Формула:

Последовательность длины n, составленная из k разных символов, первый из которых повторяется n1 – раз, второй – n2, третий – n3 раз,…k-й – nk раз (где  ) называется перестановкой с повторением из n элементов.
) называется перестановкой с повторением из n элементов.
Фор мула:

6. Граф и его элементы, способы задания графов.
Элементы графа. Способы задания графа. Подграфы.
Такая структура как граф в качестве (синонима используется также термин «сеть»), имеет самые различные применения в информатике.
Графом G называется система (V, U),
где V={v} — множество элементов, называемых вершинами графа;
U=={u} —.множество элементов, называемых ребрами графа.
- Каждое ребро определяется либо парой вершин (v1,v2), либо двумя противоположными парами (v1,v2) и (v2,v1).
- Если ребро из U представляется только одной парой (v1,v2), то оно называется ориентированным ребром, ведущим из v1 в v2. При этом v1 называется началом, а v2 -концом такого ребра.
- Если ребро U представляется двумя парами (v1,v2) и (v2,v1), то U называется неориентированным ребром. Всякое неориентированное ребро между вершинами v1 и v2 ведет как из v1 в v2, так и обратно. При этом вершины v1 и v2 являются как началами, так и концами этого ребра. Говорят, что ребро ведет какие v1 в v2, так и из v2 в v1.
|
|
|
- Всякие две вершины, которые соединяются ребром, являются смежными.
- По количеству элементов графы делятся на конечные и бесконечные.
- Граф, все рёбра которого неориентированные, называется неориентированным графом.
- Если рёбра графа определяются упорядоченными парами вершин, то такой граф называется ориентированным.
Рисунок 6 – Ориентированный граф.
- Существуют смешанные графы, состоящие как из ориентированных, так и из неориентированных рёбер.
- Если две вершины соединены двумя или более рёбрами, то эти рёбра называют параллельными.
- Если начало и конец ребра совпадают, то такое ребро называется петлёй.
- Граф без петель и параллельных рёбер называется простым.
- Если ребро определяется вершинами v1 и v2, то ребро инцидентно вершинам v1 и v2.
- Вершина, не инцидентная ни одному ребру, называется изолированной.
- Вершина, инцидентная ровно одному ребру, и само это ребро называются концевыми, или висячими.
- Ребра, которым поставлена в соответствие одна и та же пара вершин, называются кратными, или параллельными.
- Две вершины неориентированного графа v1 и v2 называются смежными, если в графе существует ребро (v1,v2).
- Две вершины ориентированного графа v1 и v2 называются смежными, если они различны и существует ребро, ведущее из вершины v1 в v2.
Рассмотрим некоторые понятия для ориентированного графа.
- Путём в графе называется такая последовательность рёбер u1,u2,…un, в которой конец каждого предыдущего ребра совпадает с началом последующего.
- Длина пути - это число рёбер, составляющих путь. Возможна длина пути =
- Путь, в котором никакое ребро не встречается дважды, называется простым, а путь, в котором кроме того не встречается дважды никакая вершина, называется элементарным.
- Контур – это конечный путь, у которого начальная вершинаv1 совпадает с конечной вершиной
- Контур называется элементарным, если все вершин, через которые он проходит, различны между собой.
|
|
|
Рисунок 7 – Ориентированный граф.
Путь:
Простой путь:
Элементарный путь:
Элементарный контур:
Контур:
Для неориентированных графов понятия «простой путь», «элементарный путь», «контур», «элементарный контур» заменяют, соответственно, понятия «цепь», «простая цепь», «цикл», «простой цикл». Граф называется связным, если для любых двух вершин существует путь (цепь), соединяющий эти вершины.
- Неориентированный связный граф без циклов называется деревом.
- Неориентированный несвязный граф без циклов - лесом.
Рисунок 9 –Лес.
Рисунок 10 – Дерево.
1. Геометрическое изображение. Как уже отмечалось, простейшим способом представления графов является их геометрическое изображение. При этом вершины графов обычно представляются точками пространства, которые помечены обозначениями вершин.
Рассмотрим пример геометрического задания графа, приведенный на рисунке 11.
Рисунок 11 - Пример геометрического задания графа
Кроме наглядного геометрического изображения и представления графов используются и другие способы задания. Они позволяют представлять графы в виде структур, которые можно хранить и обрабатывать с помощью специальных алгоритмов и программ.
7. Случайные события
Множество всех элементарных событий, имеющих место в результате случайного эксперимента, будем называть пространством элементарных событий W (элементарное событие соответствует элементарному исходу).
Случайными событиями (событиями), будем называть подмножества пространства элементарных событий W.
Пример 1. Подбросим монету один раз. Монета может упасть цифрой вверх - элементарное событие w ц (или w 1), или гербом - элементарное событие w Г (или w 2). Соответствующее пространство элементарных событий W состоит из двух элементарных событий:
W = {w ц,w Г } или W = {w 1,w 2}.
Пример 2. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий W = {w 1, w 2, w 3, w 4, w 5, w 6}, где w i- выпадение i очков. Событие A - выпадение четного числа очков, A = {w 2,w 4,w 6}, A  W.
W.
Пример 3. На отрезке [0, 1] наугад (случайно) поставлена точка. Измеряется расстояние точки от левого конца отрезка. В этом опыте пространство элементарных событий W = [0, 1] - множество действительных чисел на единичном отрезке.
|
|
|
В более точных, формальных терминах элементарные события и пространство элементарных событий описывают следующим образом.
Пространством элементарных событий называют произвольное множество W, W ={w}. Элементы wэтого множества W называют элементарными событиями.
Понятия элементарное событие, событие, пространство элементарных событий, являются первоначальными понятиями теории вероятностей. Невозможно привести более конкретное описание пространства элементарных событий. Для описания каждой реальной модели выбирается соответствующее пространство W.
Событие W называется достоверным событием.
Достоверное событие не может не произойти в результате эксперимента, оно происходит всегда.
Пример 4. Бросаем один раз игральную кость. Достоверное событие состоит в том, что выпало число очков, не меньше единицы и не больше шести, т.е. W = {w 1, w 2, w 3, w 4, w 5, w 6}, где w i- выпадение i очков, - достоверное событие.
Невозможным событием называется пустое множество Æ.
Невозможное событие не может произойти в результате эксперимента, оно не происходит никогда.
Случайное событие может произойти или не произойти в результате эксперимента, оно происходит иногда.
Пример 5. Бросаем один раз игральную кость. Выпадение более шести очков - невозможное событие Æ.
Противоположным событию A называется событие, состоящее в том, что событие A не произошло. Обозначается  ,
,  .
.
Пример 6. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, тогда событие  - выпадение нечетного числа очков. Здесь W = {w 1, w 2, w 3,w 4, w 5,w 6}, где w i- выпадение i очков, A = {w 2,w 4,w 6},
- выпадение нечетного числа очков. Здесь W = {w 1, w 2, w 3,w 4, w 5,w 6}, где w i- выпадение i очков, A = {w 2,w 4,w 6},  =
=  .
.
Несовместными событиями называются события A и B, для которых A B = Æ.
Пример 7. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, событие B - выпадение числа очков, меньшего двух. Событие AB состоит в выпадении четного числа очков, меньшего двух. Это невозможно, A = {w 2,w 4,w 6}, B = {w 1}, AB = Æ, т.е. события A и B -несовместны.
Действия со случайными событиями
|
|
|
Суммой событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одному из событий A или B. Обозначается A + B.
Пример 8. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий W = {w 1, w 2, w 3, w 4, w 5, w 6}, где элементарное событие w i- выпадение i очков. Событие A - выпадение четного числа очков, A = {w 2,w 4,w 6}, событие B - выпадение числа очков, большего четырех, B = {w 5, w 6}.
Событие A + B = {w 2,w 4, w 5, w 6} состоит в том, что выпало либо четное число очков, либо число очков большее четырех, т.е. произошло либо событие A, либо событие B. Очевидно, что A + B  W.
W.
Произведением событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одновременно событиям A и B. Обозначается AB.
Пример 9. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий W = {w 1, w 2, w 3,w 4, w 5,w 6}, где элементарное событие w i- выпадение i очков. Событие A - выпадение четного числа очков, A = {w 2,w 4,w 6}, событие B - выпадение числа очков, большего четырех, B = {w 5, w 6}.
Событие A B состоит в том, что выпало четное число очков, большее четырех, т.е. произошли оба события, и событие A и событие B, A B = {w 6} A B  W.
W.
Разностью событий A и B называется событие, состоящее из всех элементарных событий принадлежащих A, но не принадлежащих B. Обозначается A\B.
Пример 10. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, A = {w 2,w 4,w 6}, событие B - выпадение числа очков, большего четырех, B = {w 5, w 6}. Событие A\ B= {w 2,w 4} состоит в том, что выпало четное число очков, не превышающее четырех, т.е. произошло событие A и не произошло событие B, A\B  W.
W.
Очевидно, что
A + A = A, AA = A,  Æ.
Æ.
Нетрудно доказать равенства:
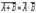 , (A+B)C= AC + BC.
, (A+B)C= AC + BC.
Определения суммы и произведения событий переносятся на бесконечные последовательности событий:
 , событие, состоящее из элементарных событий, каждое из которых принадлежит хотя бы одному из
, событие, состоящее из элементарных событий, каждое из которых принадлежит хотя бы одному из 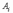 ;
;
 , событие, состоящее из элементарных событий, каждое из которых принадлежит одновременно всем
, событие, состоящее из элементарных событий, каждое из которых принадлежит одновременно всем  .
.
Вероятность события. Аксиоматическое определение вероятности
Пусть W - произвольное пространство элементарных событий, а  - такая совокупность случайных событий, для которой справедливо: W
- такая совокупность случайных событий, для которой справедливо: W 
 , AB
, AB 
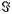 , A+B
, A+B 
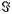 и A\B
и A\B 
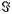 , если A
, если A 
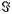 и B
и B 
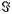 .
.
Числовая функция P, определенная на совокупности событий  , называется вероятностью, если:
, называется вероятностью, если:
P(A)  0 для любого A из
0 для любого A из  ;
;
P(W) = 1;
если A 
 и B
и B 
 несовместны, то P(A+B) = P(A) + P(B);
несовместны, то P(A+B) = P(A) + P(B);
для любой убывающей последовательности событий {Ai}из  ,
,  , такой, что
, такой, что 
 , имеет место равенство
, имеет место равенство  .
.
Тройку  называют вероятностным пространством.
называют вероятностным пространством.
Вероятность события. Классическое определение вероятности
Пусть W= {w 1, w 2, …, w s} - произвольное конечное пространство элементарных событий, A - событие, состоящее из k элементарных событий: A={w i1, w i2, …, w ik}, 1 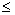 i1
i1 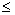 i2
i2 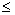 …
… 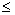 i k
i k 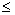 s, k = 1, 2,…, s, и пусть
s, k = 1, 2,…, s, и пусть 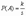 . Определенная таким образом функция P(A) удовлетворяет всем аксиомам 1-4(здесь множество
. Определенная таким образом функция P(A) удовлетворяет всем аксиомам 1-4(здесь множество  состоит из всех подмножеств множества W:
состоит из всех подмножеств множества W:  ). Таково классическое определение вероятности события A.
). Таково классическое определение вероятности события A.
|
|
|
Принята следующая формулировка классического определения вероятности: вероятностью события A называется отношение числа исходов, благоприятствующих A, к общему числу исходов.
Из приведенных определений следует: P( )=0,
)=0,  ,
,  .
.
Вероятность суммы событий
Для любых двух событий A и B справедливо:  .
.
Если события A и B несовместны, то  .
.
Вероятность произведения событий. Условная вероятность. Независимые события
Условная вероятность P(A/B) события A при условии, что событие B произошло, P(B) > 0, определяется формулой
 .
.
Для любых двух событий A и B справедливо:
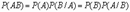 .
.
События A и B называются независимыми, если  . Для любых двух независимых, событий A и B справедливо:
. Для любых двух независимых, событий A и B справедливо:  .
.
Формула полной вероятности. Формулы Байеса
Пусть A - произвольное событие, а события B1, B2, …, Bn - попарно несовместны и образуют полную группу событий, т.е.  . Тогда имеет место следующая формула для вероятности события A- формула полной вероятности -
. Тогда имеет место следующая формула для вероятности события A- формула полной вероятности -
 , где P(Bk)>0, k=1, 2, …, n, A
, где P(Bk)>0, k=1, 2, …, n, A  B1+ B2 + …+ Bn.
B1+ B2 + …+ Bn.
Если событие A произошло, то вероятность того, что имело место событие Bk
вычисляется по формуле Байеса:  .
.
8. Определение (вычисление) вероятности наступления события.
Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможные.
Во многих случаях более удобным оказывается статистическое определение вероятности, которое связано с понятием относительной частоты появления события A в опытах. Относительная частота (частость) появления события A – это отношение числа m1 появлений события A в серии из n1 опытов к числу испытаний.
Относительная частота вычисляется по формуле:
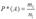
Результаты многочисленных опытов и наблюдений помогают заключить: при проведении серий из n1 испытаний, когда число nq сравнительно мало, относительная частота P*(A) принимает значения, которые могут сильно отличаться друг от друга. При однотипных массовых испытаниях во многих случаях наблюдается устойчивость относительной частоты события, т.е. с увеличением числа испытаний в сериях относительная частота P*(A) колеблется около некоторого постоянного числа P(A), причем эти отклонения тем меньше, чем дольше произведено испытаний, если не учитывать отдельные неудачные испытания (выбросы).
Вероятностью события A в статистическом смысле называется число P(A), относительно которого стабилизируется (устанавливается) относительная частота P*(A) при неограниченном увеличении числа опытов.
Под вероятностью события в статистическом смысле понимается почти достоверный предел его относительной частоты при неограниченно растущем числе испытаний. Таким образом, почти достоверно, что относительная частота события приближенно совпадает с его статистической вероятностью, если число испытаний достаточно велико. Поэтому, в практических задачах за вероятность события A принимается относительная частота P*(A) при достаточно большом числе испытаний.
Легко убедиться, что свойства вероятности, вытекающие из классического определения вероятности, сохраняются и при статистическом определении вероятности.
Если вероятность некоторого события близка к нулю, то, в соответствии со сказанным следует, что при единичном испытании в подавляющем большинстве случаев такое событие не наступит. Естественно, наступает вопрос: насколько малой должна быть вероятность, чтобы можно было считать невозможным наступление некоторого события в единичном испытании? Ответ на него не однозначен и зависит от тех потерь, которые будут иметь место, если это событие все-таки произойдет. Достаточно малую вероятность, при которой наступление события можно считать практически невозможным, называют уровнем значимости. На практике уровень значимости обычно принимают равным 0,05 (пятипроцентный уровень) или 0,01 (однопроцентный уровень).
При широких предположениях доказывается, что вероятности события в классическом и статистическом смыслах совпадают.
9.Вычисление веротностей событий и комбинаторики
Примеры решения задач по теме «Элементы комбинаторики. События и их вероятности»
Задача 1
В 11-м классе 30 человек. 18 человек изучают английский язык, 16 – немецкий, 9 – оба языка. Сколько человек изучают а) только английский язык, б) только немецкий язык, в) не изучают ни одного языка?
Решение.
а) поскольку 18 человек изучают английский, из них 9 изучают и английский и немецкий, то 18–9=9 человек изучают только английский язык;
б) поскольку 16 человек изучают немецкий, из них 9 изучают и немецкий и английский, то 16–9=7 человек изучают только немецкий язык;
в) поскольку в классе 30 человек, из них 9 изучают только английский, 7 – только немецкий, 9 – оба языка, то 30 – (9+7+9) = 5 человек не изучают ни одного языка.
Задача 2
Сколькими способами можно переставить буквы в слове «фикус»?
Решение. В данном случае необходимо найти число перестановок из 5 букв, а поскольку в слове «фикус» все буквы разные, то число перестановок определяем по формуле: P5=5!=1*2*3*4*5=120.
Задача 3
Сколькими способами можно переставить буквы в слове «ответ»?
Решение. Необходимо найти число перестановок из 5 букв, но в отличие от задачи 2, здесь имеются повторяющиеся буквы – буква «а» повторяется дважды. Поэтому число способов определим по формуле перестановок с повторениями: P5(1, 2, 1, 1) = 5! / 2! = 60.
Задача 4
В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по производной. Найдите вероятность того, что в случайно выбранном на экзамене билете учащемуся не достанется вопрос по производной.
Решение. В данном случае число благоприятных исходов равно (25-10)=15, общее число событий – 25.
Вероятность события А = {учащемуся не достанется вопрос по производной} находим как отношение: Р(А)=15/25=0,6.
Задача 5
В ящике имеется 15 деталей, среди которых 8 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
Решение. Событие А = {извлечены три окрашенных детали}.
Общее число всех возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 3 детали из 15:
n = С153=15! / 3!(15-3)!=15! / (3!*12!) = 13*7*5=455.
Число благоприятных исходов равно числу способов, которыми можно извлечь 3 детали из 8 окрашенных:
m = С83=8! / 3!(8-3)!= 8! / (3!*5!)=7*8=56.
Вероятность события А находим как отношение: Р(А) = m/n= 56/455≈0,12
Задача 6
Среди 17 студентов группы, из которых 8 – девушки, разыгрывается 7 билетов в театр. Какова вероятность того, что среди обладателей билетов окажутся 4 девушки и 3 юношей?
Решение. Событие А = {среди обладателей билетов ровно 4 девушки}.
Общее число возможных элементарных исходов розыгрыша равно числу способов, которыми можно выбрать 7 человек из всех студентов группы, т. е. из 17: n = С177=17! / 7!(17-7)!= 17! / (7!*10!)=19448.
Число благоприятных исходов (среди 7 обладателей билетов 4 девушки и 3 юношей) найдем, учитывая, что 4-х девушек их 8 можно выбрать С84 способами, а 3-х юношей из 9 можно выбрать С93 способами. Следовательно, m = С84 *С93 = 8!9! / 4!(8-4)!3!(9-3)! = 5880.
Вероятность события А находим как отношение: Р(А) = m/n= 5880/19448≈0,3
|
|
|


