 |
Геометрическая вероятность
|
|
|
|
Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т.д.).
Приведем формальное определение вероятностей для испытаний с бесконечным числом исходов. В подобных случаях пространство элементарных исходов может быть областью G, а под событием A можно понимать исходы, входящие в областьg.
Пусть на область G наугад бросается «точка». Какова вероятность того, что эта точка попадет в область g, являющуюся частью области G?
1. Пусть отрезок g, длину которого обозначим как lg, составляет часть отрезка G длина которого lG. На отрезок G наудачу поставлена точка. Это означает выполнение следующих предположений:
-поставленная точка может оказаться в любой точке отрезка G;
-вероятность попадания точки на отрезок g пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка G.
В этих предположениях вероятность попадания точки на отрезок g определяется равенством 
.
2. Пусть плоская фигура g с площадью Sg составляет часть плоской фигуры G, площадь которой SG. На фигуру G наудачу брошена точка. Это означает выполнение следующих предположений:
-брошенная точка может оказаться в любой точке фигуры G;
-вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно фигуры G, ни от формы g.
В этих предположениях вероятность попадания точки на фигуру g определяется равенством 
.
3. Аналогично вводится понятие геометрической вероятности при бросании точки в пространственную область G объема VG, содержащую область g объема Vg: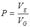 
.
|
|
|
В общем случае понятие геометрической вероятности вводится следующим образом.
Пусть 
– некоторое множество (базис), а 
– s-алгебра его подмножеств. Функция 
называется мерой, на 
, если она удовлетворяет условиям:
-Для любого множества 
его мера неотрицательна: 
;
-Для любого счетного набора попарно непересекающихся множеств 
мера их суммы равна сумме их мер: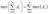 
– свойство счетной аддитивности.
Обозначим меру области g (длину, площадь, объем) через mes(g), а меру области G– через mes(G); обозначим через A событие «попадание брошенной точки в область g, которая содержится в области G». Вероятность события A, т.е. вероятность попадания в область gточки, брошенной в область G, определяется формулой: 
2) Рассмотрим, например, на плоскости некоторую область G, имеющую площадь 
, и внутри области G область g с площадью 
. Пусть в область G наудачу бросается точка. При этом попадание точки в область G – достоверное событие, а в g – случайное. Предполагается, что все точки области G Равноправны, т. е. наудачу брошенная точка может попасть в любую точку области G, и вероятность события A – попадания точки в область g – пропорциональна площади этой области и не зависит от ее расположения и формы (рис.1).
Геометрической вероятностью события A называется отношение площади области g к площади области G, т. е.
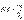(2)
Область g называется Благоприятствующей (благоприятной) событию A.
Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (прямая, отрезок) и трехмерной (некоторое тело в пространстве). Обозначая меру (длину, площадь, объем) области через mes, можно записать
(3)
11. Теоремы сложения вероятностей.
Несколько событий называются несовместимыми, если появление одного из них исключает возможность появления остальных.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий
|
|
|
P (AÈB) =P (A) +P (B). (2.1)
Если имеется счетное множество несовместных событий A 1,..., An, то
. (2.2)
Из правила сложения вероятностей вытекает, что если события A1, A2, …, An несовместны и образуют полную группу, то сумма их вероятностей равна единице; т.е. если
AiּAj =О при i≠j, то
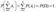(2.3)
В частности, если два события А и 
противоположны, то они образуют полную группу несовместных событий и
(2.4)
Тогда
(2.5)
Вероятность суммы двух совместных событий равна сумме вероятностей каждого из событий минус вероятность их совместного появления:
. ошибка-пересечение (2.6)
2) Противоположным к событию A называется такое событие 
, которое заключается в том, что событие A не происходит.
События Ak (k =1, 2,..., n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие.
При преобразовании выражений можно пользоваться следующими тождествами:
.
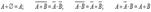3) Рассмотрим некоторое случайное событие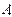 
и пусть его вероятность 
известна. Тогда вероятность противоположного события 
определяется по формуле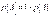 
Доказательство. В силу несовместности 
и 
, учитывая аксиомы, получаем:
и, следовательно, 
.
Следствие: 
, то есть вероятность невозможного события равна нулю.
4) Теорема. Вероятность суммы несовместных событий равна сумме вероятностей этих событий: 
, где 
и 
- несовместные события.
Замечание. Теорема верна и для n попарно несовместных событий.
Следствие. Рассмотрим противоположные события A и 
. Эти события несовместны, причем событие 
достоверное. Отсюда 
. Но 
, поэтому 
.
5) Теорема. Вероятность суммы двух совместимых событий А и В равна сумме вероятностей этих событий минус вероятность их произведения:
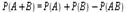
Если события А и В несовместимы, то их произведение АВ — невозможное событие и, следовательно, Р (А В) = 0, т. е.
P(A+B)=P(A)+P(B).
Умножение вероятностей.
1) 
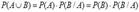ошибка-пересечение (2.9)
Вероятность произведения (пересечения, совмещения) двух событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого (правило умножения вероятностей).
Правило умножения вероятностей может быть обобщено на случай произвольного числа событий
(2.10)
т.е. вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место.
|
|
|
Событие A называется независимым от события B, если его вероятность не зависит от того, произошло событие B или нет, т.е. P(B / A)=P(B).
Для независимых событий правило произведения вероятностей принимает вид:
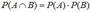.(2.11)
Несколько событий A1, A2, …, An называются независимыми, если любое из них не зависит от любой комбинации (произведения) любого числа других. Для независимых событий правило умножения принимает вид:
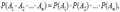(2.12)
или
(2.13)
т.е. вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий.
Заметим, что если имеется несколько событий A1, A2, …, An, то их попарная независимость (т.е. независимость любых двух событий Ai и Aj, i≠j) еще не означает их независимости в совокупности.
2) Для зависимых событи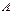й 
и 
верно следующее: 
.
Это означает, что вероятность совместного наступления двух событий равна произведению вероятности одного события на условную вероятность другого события, вычисленную при условии, что произошло первое событие.
Условная вероятность
1) Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.
2) Пусть 
— фиксированное вероятностное пространство. Пусть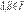 
два случайных события, причём 
. Тогда условной вероятностью события A при условии события B называется
.
Полная вероятность
Если событие А может произойти только при выполнении одного из событий 
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
.
Эта формула называется формулой полной вероятности.
Вновь рассмотрим полную группу несовместных событий 
, вероятности появления которых 
. Событие А может произойти только вместе с каким-либо из событий 
, которые будем называть гипотезами. Тогда по формуле полной вероятности
Если событие А произошло, то это может изменить вероятности гипотез
|
|
|
.
По теореме умножения вероятностей
,
откуда
.
Аналогично, для остальных гипотез
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез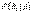 
называются апостериорными вероятностями, тогда как 
- априорными вероятностями.
Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через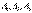 
обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
Можно применить формулу полной вероятности, причем в наших обозначениях:
Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:
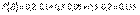
Повторение испытаний.
1) ПОВТОРЕНИЕ НЕЗАВИСИМЫХ ОПЫТОВ. Несколько опытов называются независимыми, если вероятность исхода опыта не зависит от того, какие исходы имели другие опыты. Рассмотрим случай, когда вероятности исходов опытов постоянны и не зависят от номера опыта.
Пусть один тот же опыт проводятся n раз. В каждом опыте некоторые события А1, А2, …, Аr появляется с вероятностями р1, р2, …, рп. Будем рассматривать не результат каждого конкретного опыта, а общее число появлений событий А1, А2, …, Аr.
Рассмотрим случай с двумя возможными исходами опытов, т.е. в результате каждого опыта событие A появляется с вероятностью р и не появляется с вероятностью q=1-p. Вероятность P(n,k) того, что в последовательности из n опытов интересующее нас событие произойдет ровно k раз (безразлично, в какой последовательности), равна (формула Бернулли)
. (4.1)
Следствия из формулы Бернулли.
1. Вероятность того, что событие А наступит менее k раз
(4.2)
2. Вероятность того, что событие наступит более k раз
(4.3)
3. Вероятность того, что в n опытах схемы Бернулли, событие А появится от k1 до k2 раз
. (4.4)
4. Вероятность того, что в n опытах событие А появится хотя бы один раз, определяется формулой
(4.5)
Число к0, которому соответствует максимальная биномиальная вероятность 
, называется наивероятнейшим числом появления события А. При заданных n и p это число определяется неравенствами: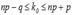 
. (4.6)
16. Локальная и интегральная формулы
Если количество независимых испытаний достаточно большое применения формулы Бернулли становится трудоемким. Для упрощения вычислений применяют локальную и интегральную теоремы Лапласа, которые дают близкий к формуле Бернулли результат при большом количестве испытаний и не требуют больших вычислений.
|
|
|
ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА
Вероятность того, что в 
независимых испытаниях с вероятностью появления события 
равной 
событие наступит ровно 
раз (безразлично в какой последовательности) определяется по приближенной формуле
где
– Функция Гаусса,
– аргумент функции Гаусса;
– вероятность противоположного события 
.
Формулу 
называют локальной формулой Лапласа.
Функция 
обладает следующими свойствами:
1) она является четной функцией 
;
2) для значений аргумента больше четырех она сколь угодно мала 
Теорему Лапласа рекомендуется применять при значениях произведения больше девяти
ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА-ЛАПЛАСА
Вероятность, что в независимых испытаниях событие 
с вероятностью появления 
наступит не менее 
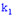раз и не более 
(независимо от последовательности появления) приближенно определяется зависимостью
где 
– интегральная функция Лапласа;
– аргументы интегральной функции распределения;
– вероятность невыполнения события .
Функция 
обладает следующими свойствами:
1) она является нечетной функцией
2) для аргументов больше пяти она равна 0,5
Значение обеих функций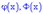 
находят из таблиц в которых функции с достаточной точностью протабульовани.
--------------------------------
Рассмотрим задачи на применение каждой из теорем.
Пример 1. Есть 100 лунок по которым случайным образом разбрасывают 30 шариков. Каждый шарик с равной вероятностью может попасть в любую лунку (в одну лунку попадает не более одного шарика). Найти вероятность того, что в выбранную лунку попадет ровно один шарик.
Решение. Проводится 
независимых бросков шариков с одинаковой вероятностью попадания при каждом броске
Вероятность попадания в лунку ровно одного шарика определим по локальной формулой Лапласа:
Для этого определяем составляющие
и подставим в зависимость
--------------------------------
Пример 2. Проводится 200 независимых опытов с вероятностью успеха в каждом 24%. Какова вероятность успешного проведения 50 опытов?
Решение. По условию 
находим составляющие формулы Лапласа
Подставляя в формулу, находим
--------------------------------
Пример 3. Вероятность выхода из строя за смену одного станка равна 0,1. Определить вероятность выхода из строя от 2 до 13 станков при наличии 100 станков.
Решение. Записываем входные данные
Для подобных примеров применяем интегральную формулу Муавра-Лапласа и находим вероятность
--------------------------------
Решение задач по приведенным теоремам позволяет при большом количестве испытаний находить приближенное значение вероятности. Локальная теорема необходима при определении конкретного количества появления событий, интегральная теорема Муавра-Лапласа - в случаях, когда задан диапазон возможного количества появлений события. Таблицы табулирования функций, применяемых в формулах можно найти в сборниках по теории вероятностей и интернете.
Если вероятность 
появления события 
в отдельном испытании достаточно близка к нулю 
, то даже при больших значениях количества испытаний вероятность, вычисляемая по локальной теореме Лапласа, оказывается недостаточно точной. В таких случаях используют формулу, выведенную Пуассоном.
ТЕОРЕМА ПУАССОНА
Если вероятность 
наступления события 
в каждом испытании постоянна, но достаточно мала, число независимых испытаний достаточно велико, при этом сочетания 
меньше десяти то вероятность того, что в количестве испытаниях событие наступит ровно 
раз примерно равна
где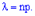 
Для формулы Пуассона используют таблицы табулирования функции 
.
-------------------------------
Рассмотрим примеры типичных для студентов задач.
Пример 1. Автобиография писателя издается тиражом в 1000 экземпляров. Для каждой книги вероятность быть неправильно сброшюрованной равна 0,002. Найти вероятность того, что тираж содержать ровно 7 бракованных книг.
Решение. Проверим выполнение условия теоремы Пуассона. Для входных значений
получим
что условия выполняются.
По табличным значениям функции Пуассона находим вероятность
Применения к этому событию локальную теорему Лапласа получим
Точное значение вероятности определяем по формуле Бернулли
Из анализа трех методов следует, что формула Пуассона дает более точнее приближения, чем формула Лапласа. Именно поэтому ее рекомендуют применять для отыскания вероятности в такого сорта задачах.
-------------------------------
Пример 2. Вероятность изготовления нестандартной детали равна 0,004. Найти вероятность того, что среди 1000 деталей окажется 5 нестандартных.
Решение. Имеем даные 
, которые удовлетворяют требования теоремы Пуассона 
По таблице функции Пуассона при 
получим:
Найдем вероятность того же события по локальной теореме Лапласа.
Для 
,
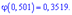
искомая вероятность: 
Точное значение вычисляем согласно формулы Бернулли:
Таким образом, формула Пуассона дает гораздо более точное приближение, чем формула Лапласа.
Пример 3. Станок штампует детали. Вероятность того, что изготовленная деталь бракованная, равна 0,02. Какова вероятность того, что среди 200 деталей окажется 5 бракованных?
Решение. Есть 
, есть удовлетворяются требования теоремы
По таблице функции Пуассона при получим:
----------------------------------------------
Используйте формулу Пуассона в тех задачах, где она более уместна. Всегда проверяйте выполнения условия теоремы Пуассона, при значениях которые не удовлетворяют условие формула дает большую погрешность при вычислении вероятности. Для проверки результата применяйте формулу Бернулли, она более точна и с ее результатом найденную вероятность по формуле Пуассона лучше всего сравнивать. Если погрешность невелика, тогда Вы все сделали правильно, в противном случае придется вычислять снова или найти слабое место и исправить ошибки.
17.Понятие случайной дискретной величины
Рассмотрим случайную величину * 
, возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2,..., xn,.... Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1,2,...) равно вероятности того, что величина 
примет значение xi
Такая случайная величина называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2,..., xn,.... Так как в каждом из испытаний случайная величина принимает всегда какое-либо значение из области ее изменения, то
Пример 1. Случайная величина — число очков, выпадающих при однократном бросании игральной кости. Возможные значения — числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения? (Решение)
Пример 2. Пусть случайная величина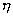 
- число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений 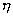состоит из 2-х чисел 0 и 1: 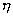=0, если событие A не произошло, и 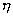=1, если событие A произошло. Таким образом,
Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить событие A. Пусть вероятность наступления события A при каждом испытании равна p. Рассмотрим случайную величину — число наступлений события A при n независимых испытаниях. Область изменения состоит из всех целых чисел от 0 до n включительно. Закон распределения вероятностей р(m) определяется формулой Бернулли (13'):
Закон распределения вероятностей по формуле Бернулли часто называют биномиальным, так как Pn(m) представляет собой m-й член разложения бинома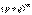 
.
Пусть случайная величина может принимать любое целое неотрицательное значение, причем
| (17) |
где 
— некоторая положительная постоянная. В этом случае говорят, что случайная величина распределена по закону Пуассона, Заметим, что при k=0следует положить 0!=1.
Как мы знаем, при больших значениях числа n независимых испытаний вероятность Pn(m) наступления m раз события A удобнее находить не по формуле Бернулли, а по формуле Лапласа. Однако последняя дает большие погрешности при малой вероятности р появления события А в одном испытании. В этом случае для подсчета вероятности Pn(m) удобно пользоваться формулой Пуассона, в которой следует положить 
.
Формулу Пуассона можно получить как предельный случай формулы Бернулли при неограниченном увеличении числа испытаний n и при стремлении к нулю вероятности 
.
18. Характеристика и свойства случайной дискретной величины
Закон распределения (функция распределения и ряд распределения или плотность веро-ятности) полностью описывают поведение случайной величины. Но в ряде задач доста-точно знать некоторые числовые характеристики исследуемой величины (например, ее среднее значение и возможное отклонение от него), чтобы ответить на поставленный во-прос. Рассмотрим основные числовые характеристики дискретных случайных величин.
Математическое ожидание.
Определение 7.1. Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности:
М (Х) = х 1 р 1 + х 2 р 2 + … + хпрп. (7.1)
Если число возможных значений случайной величины бесконечно, то, если полученный ряд сходится абсолютно.
Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.
Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего.
Замечание 3. Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непрерывных случайных величин.
Пример 1. Найдем математическое ожидание случайной величины Х – числа стандартных деталей среди трех, отобранных из партии в 10 деталей, среди которых 2 бракованных. Составим ряд распределения для Х. Из условия задачи следует, что Х может принимать значения 1, 2, 3. Тогда
Пример 2. Определим математическое ожидание случайной величины Х – числа бросков монеты до первого появления герба. Эта величина может принимать бесконечное число значений (множество возможных значений есть множество натуральных чисел). Ряд ее распределения имеет вид:
| Х | … | п | … | ||
| р | 0,5 | (0,5)2 | … | (0,5) п | … |
Тогда
..+
+ 
(при вычислении дважды использовалась формула суммы бесконечно убывающей геометрической прогрессии:, откуда).
Свойства математического ожидания.
1) Математическое ожидание постоянной равно самой постоянной
Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М (С) = С ·1 = С.
2) Постоянный множитель можно выносит за знак математического ожидания:
М (СХ) = С М (Х). (7.3)
Доказательство. Если случайная величина Х задана рядом распределения
| xi | x 1 | x 2 | … | xn |
| pi | p 1 | p 2 | … | pn |
то ряд распределения для СХ имеет вид:
| Сxi | Сx 1 | Сx 2 | … | Сxn |
| pi | p 1 | p 2 | … | pn |
Тогда М (СХ) = Сх 1 р 1 + Сх 2 р 2 + … + Схпрп = С (х 1 р 1 + х 2 р 2 + … + хпрп) = СМ (Х).
Определение 7.2. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы.
Определение 7.3. Назовем произведением независимых случайных величин Х и Y случайную величину XY, возможные значения которой равны произведениям всех возможных значений Х на все возможные значения Y, а соответствующие им вероятности равны произведениям вероятностей сомножителей.
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M (XY) = M (X) M (Y). (7.4)
Доказательство. Для упрощения вычислений ограничимся случаем, когда Х и Y принимают только по два возможных значения:
| xi | x 1 | x 2 |
| pi | p 1 | p 2 |
| уi | у 1 | у 2 |
| gi | g 1 | g 2 |
Тогда ряд распределения для XY выглядит так:
| ХY | x 1 y 1 | x 2 y 1 | x 1 y 2 | x 2 y 2 |
| p | p 1 g 1 | p 2 g 1 | p 1 g 2 | p 2 g 2 |
Следовательно, M (XY) = x 1 y 1· p 1 g 1 + x 2 y 1· p 2 g 1 + x 1 y 2· p 1 g 2 + x 2 y 2· p 2 g 2 = y 1 g 1(x 1 p 1 + x 2 p 2) + + y 2 g 2(x 1 p 1 + x 2 p 2) = (y 1 g 1 + y 2 g 2) (x 1 p 1 + x 2
