 |
Медиана и мода непрерывной случайной величины
|
|
|
|
Мода — значение во множестве наблюдений, которое встречается наиболее часто
Мо = XMо + hМо * (fМо - fМо-1): ((fМо - fМо-1) + (fМо - fМо+1)),
здесь XMо — левая граница модального интервала, hМо — длина модального интервала, fМо-1 — частота премодального интервала, fМо — частота модального интервала, fМо+1 — частота послемодального интервала.
Модой абсолютно непрерывного распределения называют любую точку локального максимума плотности распределения. Для дискретных распределений модой считают любое значение ai, вероятность которого pi больше, чем вероятности соседних значений
Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т.е.
Ме=(n+1) /2 Р(Х < Ме) = Р(X > Ме)
Равномерно распределенная НСВ
Равномерное распределение. Непрерывная случайная величина 
называется равномерно распределенной на отрезке 
(
), если ее функция плотности распределения (рис. 1.6, а) имеет вид [3]:
Обозначение: 
– СВ 
распределена равномерно на 
.
Соответственно функция распределения на отрезке (рис. 1.6, б):
Рис. 1.6. Функции случайной величины, распределенной равномерно на [ a, b ]: а – плотности вероятностей f (x); б – распределения F (x)
Математическое ожидание и дисперсия данной СВ определяются выражениями:
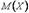, в силу симметрии функции плотности, совпадает с медианой. Моды равномерное распределение не имеет
Пример 4. Время ожидания ответа на телефонный звонок – случайная величина, подчиняющаяся равномерному закону распределения в интервале от 0 до 2 минут. Найти интегральную и дифференциальную функции распределения этой случайной величины.
|
|
|
27.Нормальный закон распределения вероятностей
Непрерывная случайная величина x имеет нормальльное распределение с параметрами: m,s > 0, если плотность распределения вероятностей имеет вид:
где: m – математическое ожидание, s– среднеквадратическое отклонение.
Нормальное распределение называют еще гауссовским по имени немецкого математика Гаусса [1777-1855]. Тот факт, что случайная величина имеет нормальное распределение с параметрами: m, 
, обозначают так: N (m,s), где: m=a=M[X]; 
Достаточно часто в формулах математическое ожидание обозначают через а. Если случайная величина распределена по закону N(0,1), то она называется нормированной или стандартизированной нормальной величиной. Функция распределения для нее имеет вид:
График плотности нормального распределения, который называют нормальной кривой или кривой Гаусса, изображен на рис.5.4.
Рис. 5.4. Плотность нормального распределения
свойства случайной величины, имеющей нормальный закон распределения.
1. Если 
, то для нахождения вероятности попадания этой величины в заданный интервал (х1;х2) используется формула:
.
2. Вероятность того, что отклонение случайной величины 
от ее математического ожидания 
не превысит величину 
(по абсолютной величине), равна:
.
3. "Правило трех сигм". Если случайная величина 
, то практически достоверно, что ее значения заключены в интервале (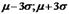
). (Вероятность выхода за эти границы составляет 0,0027.) Правило позволяет, зная параметры (
и 
), ориентировочно определить интервал практических значений случайной величины.
Показательное распределение
Случайная величина X имеет экспоненциальное распределение с параметром 
, если её плотность имеет вид
.
Интегрируя плотность, получаем функцию экспоненциального распределения:
сновные характеристики показательного распределения:
Графики плотности и функции полученного показательного распределения
|
|
|
|
|
|
