Числовые характеристики случайных величин, имеющих некоторые стандартные законы распределения.

1. Биномиальное распределение.

Для дискретной случайной величины Х, представляющей собой число появлений события А в серии из п независимых испытаний (см. лекцию 6), М (Х) можно найти, используя свойство 4 математического ожидания. Пусть Х ₁ – число появлений А в первом испытании, Х ₂ – во втором и т.д. При этом каждая из случайных величин Х_i задается рядом распределения вида

Xi
pi	q	p

Следовательно, М (Х_i) = p. Тогда

Аналогичным образом вычислим дисперсию: D (X_i) = 0²· q + 1²· p – p ² = p – p ² = p (1 – p), откуда по свойству 4 дисперсии

2. Закон Пуассона.

Если р (Х = т) = 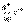, то М (Х) = (использовалось разложение в ряд Тейлора функции е^х).

Для определения дисперсии найдем вначале М (Х ²) =

Поэтому D (X) = a ² + a – a ² = a.

Замечание. Таким образом, обнаружено интересное свойство распределения Пуассона: математическое ожидание равно дисперсии (и равно единственному параметру а, определяющему распределение).

3. Равномерное распределение.

Для равномерно распределенной на отрезке [ a, b ] непрерывной случайной величины, то есть математическое ожидание равномерно распределенной случайной величины равно абсциссе середины отрезка [ a, b ].

Дисперсия

.

4. Нормальное распределение.

Для вычисления математического ожидания нормально распределенной случайной величины воспользуемся тем, что интеграл Пуассона.

 

(первое слагаемое равно 0, так как подынтегральная функция нечетна, а пределы интегрирования симметричны относительно нуля).

.

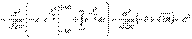Следовательно, параметры нормального распределения (а и σ) равны соответственно математическому ожиданию и среднему квадратическому отклонению исследуемой случайной величины.

20. Функции плотности случайной непрерывной величины.

Как известно, случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначают заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными буквами (x, y, z). различают непрерывные и дискретные случайные величины.

Непрерывной случайной величиной называется случайная величина Х, если ее функция распределения (интегральная функция распределения) представима в виде:

где f (x) – некоторая неотрицательная функция, такая что

Функция f (x) называется плотностью распределения вероятностей случайной величины X (дифференциальной функцией распределения).

Вероятность того, что непрерывная случайная величина X принимает значение в заданном промежутке, вычисляется следующим образом:

Примеры распределений вероятностей непрерывной случайной величины Х:

· равномерное распределение вероятностей непрерывной случайной величины;

· показательное распределение вероятностей непрерывной случайной величины;

· нормальное распределение вероятностей непрерывной случайной величины.

При решении задач широко используют числовые характеристики непрерывных случайных величин (таблица 1).

Таблица 1 - Числовые характеристики непрерывных случайных величин
Числовая характеристика	Обозначение и формула
Математическое ожидание непрерывной случайной величины Х
Если все возможные значения Х принадлежат интервалу (а, b), то математическое ожидание вычисляют
Дисперсия непрерывной случайной величины Х
иначе
Если все возможные значения Х принадлежат интервалу (а, b), то дисперсию вычисляют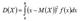
иначе
Среднее квадратическое отклонение непрерывной случайной величины Х

21. Интегральная функция распределения случайной непрерывной величины.

Все по отдельности возможные значения непрерывных случайных величин перечислить нельзя - их бесконечно много. Поэтому естественно указывать вероятности не для отдельных значений, а для целых интервалов. Рассмотрим значения с.в.Х такие, что Х<х. Вероятность события X<х зависит от x, т.е. является функцией x. Эта функция и называется интегральной функцией распределения и обозначается через F(x). Итак, по определению

F(x)=P(X<x)

Для наглядности можно представить себе такую картину. На чис­ловую ось наугад бросаем точку (в соответствии с некоторым за­коном распределения). ТогдаF(x), для каждого x указывает вероятность того, что точка упадёт левее x

Непосредственно из определения интегральной функции распределения вытекают следующие свойства F(x):

1. . Это следует из того, что F(x)=P(X<x), а вероятность P – есть число заключённое между нулём и единицей.

Легко видеть, что

так как события

X<-¥ и X<¥

являются соответственно невозможным и достоверным.

2. Интегральная функция распределения является неубывающей, т.е. при . В самом деле, пусть . Событие 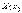можно разложить на два события: и . События эти несовместны, поэтому по теореме сложения вероятностей имеем

или

Так как в правой части стоит неотрицательная величина, то

1. Следствие: Вероятность того, что сл. величина X примет значение из интервала [a,b] равна приращению интегральной функции распределения на этом интервале.

2. Следствие. Если функция F(x) непрерывна, то вероятность того, что непрерывная случайная величина примет одно единственное значение равна нулю. Это следует из того, что

, при Dx®0, следовательно

Р(х Р(Х=х)=0.

Похожая ситуация в геометрии. Геометрическая точка не имеет размера, а интервал состоящий из точек имеет длину отличную от нуля. Так и для непрерывных случайных величин одно единственное значение имеет нулевую вероятность, а интервал имеет вероятность отличную от нуля. В общем случае график функции F(x) изображен ниже. Если рассмотреть на оси Х интервалы одинаковой длины, то вероятность попасть в какой-то из них для с.в.Х будет тем больше, чем больше окажется приращение функции F(x) на этом интервале.

Пример 1. Показательный закон распределения определяется интегральной функцией распределения , где l>0 некоторый параметр. График этой функции имеет вид:

 

Из графика видно, что P(X<0)=F(0)=0 т.е. X принимает только неотрицательные значения. Кроме того, значения близкие к нулю более вероятны, нежели все другие. Функция возрастает вблизи нуля наиболее быстро и ее приращения, равные вероятности попадания в интервал, для интервалов расположенных вблизи нуля будут больше, чем для таких же интервалов, расположенных в любом другом месте числовой оси. По такому закону распределено, например, время безотказной работы бытовых приборов и других сложных устройств.

Дополнение. Показательный закон распределения тесно связан с рассмотренным выше распределением Пуассона. Пусть случайные события на оси времени распределены по закону Пуассона с параметром 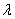, т.е. вероятность того, что на отрезке времени длительности х произойдет m событий равна P(m)= 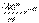..Зафиксируем момент наступления события и найдем вероятность того, что до момента наступления следующего события пройдет времени больше, чем х. Это означает, что за время х не появится ни одного события: Р(0)= . Тогда вероятность того, что между моментами появления событий времени будет меньше х равна 1- е (как вероятность противоположного события). В результате приходим к показательному распределению P(X<x)=F(x)= 1-e .

Поток, в котором интервалы между моментами наступления последовательных событий распределены по показательному закону, называется простейшим или Пуассоновским. Итак, если события во времени или пространстве распределены по закону Пуассона, то интервалы между последовательными событиями распределены по показательному закону.

Замечание 1. Если дискретная случайная величина имеет закон распределения, то её интегральная функция распределения имеет вид,

где скачки функции равны вероятностям соответствующих значений X.

Интегральная функция непрерывной случайной величины представляет собой непрерывную функцию,.для дискретной случайной величины она имеет вид ступенчатой функции. Можно привести примеры таких сл. величин, интегральная функция которых не везде является непрерывной неубывающей функцией, а в некоторых точках имеет разрывы. Такие величины называют смешанными случайными величинами.

22. Характеристика случайной непрерывной величины

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: