 |
Числовые характеристики непрерывных случайных величин
|
|
|
|
Для непрерывных случайных величин, так же, как и для дискретных, используют понятия математического ожидания и дисперсии.
Математическим ожиданием непрерывной случайной величины 
называется значение интеграла:
,
где 
– плотность вероятности.
Дисперсией непрерывной случайной величины называется значение интеграла:
.
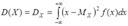Среднее квадратичное отклонение непрерывной случайной величины 
вычисляется как корень квадратный из дисперсии:
.
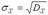Мода (
) непрерывной случайной величины – это такое ее значение, которому соответствует максимальное значение ее плотности вероятности.
Медианой (
) непрерывной случайной величины 
называется такое ее значение, которое определяется равенством:
.
Основные свойства математического ожидания и дисперсии непрерывных случайных величин остаются такими же, как и для дискретных случайных величин.
Начальные и центральные моменты для непрерывных случайных величин находятся по формулам:
Основные примеры распределений непрерывной случайной величины
Равномерное распределение
Непрерывная случайная величина считается равномерно распределенной, если ее плотность вероятности имеет вид:
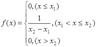
Математическое ожидание случайной величины, имеющей равномерное распределение:
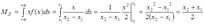
Дисперсия может быть вычислена следующим образом:
Среднее квадратичное отклонение будет иметь вид:
.
Показательное распределение
Показательным (экспоненциальным) распределением непрерывной случайной величины называется такое распределение, которое описывается следующим выражением для плотности вероятности:
|
|
|
,
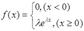где 
– постоянная положительная величина.
Функция распределения вероятности в этом случае имеет вид:
Математическое ожидание случайной величины, имеющей экспоненциальное распределение, получаем на основании общей формулы с учетом того, что 
при 
:
.
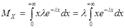Интегрируя это выражение по частям, находим: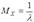 
.
Дисперсию для экспоненциального распределения можно получить, используя выражение:
.
Подставляя выражение для плотности вероятности, находим:
Вычисляя интеграл по частям, получаем: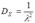 
.
23. Функция плотности и функция распределения непрерывной случайной величины.
Пусть имеется непрерывная случайная величина 
с функцией распределения 
, которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от 
до 
:
,
т.е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать 
к нулю. В пределе получим производную от функции распределения:
. (5.4.1)
Введем обозначение:
. (5.4.2)
Функция 
- производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины 
.
Термины «плотность распределения», «плотность вероятности» становятся особенно наглядными при пользовании механической интерпретацией распределения; в этой интерпретации функция 
буквально характеризует плотность распределения масс по оси абсцисс (так называемую «линейную плотность»). Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис. 5.4.1).
Рис. 5.4.1.
|
|
|
Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.
Рассмотрим непрерывную случайную величину 
с плотностью распределения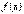 
и элементарный участок 
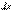, примыкающий к точке (рис. 5.4.2). Вероятность попадания случайной величины 
на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна 
. Величина 
называется элементом вероятности. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок 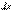(рис. 5.4.2).
Рис. 5.4.2.
Выразим вероятность попадания величины на отрезок от 
до 
(рис 5.4.3) через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем этом участке, т.е. интегралу:
(5.4.3)
*) Так как вероятность любого отдельного значения непрерывной случайной величины равна нулю, то можно рассматривать здесь отрезок 
, не включая в него левый конец, т.е. отбрасывая знак равенства в 
.
Геометрически вероятность попадания величины на участок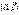 
равна площади кривой распределения, опирающейся на этот участок (рис. 5.4.3.).
Рис. 5.4.3.
Формула (5.4.2.) выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению
,
откуда по формуле (5.4.3) имеем:
. (5.4.4)
Геометрически 
есть не что иное, как площадь кривой распределения, лежащая левее точки (рис. 5.4.4).
Рис. 5.4.4.
Укажем основные свойства плотности распределения.
1. Плотность распределения есть неотрицательная функция:
.
Это свойство непосредственно вытекает из того, что функция распределения 
есть неубывающая функция.
2. Интеграл в бесконечных пределах от плотности распределения равен единице:
.
Это следует из формулы (5.4.4) и из того, что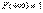 
.
Геометрически основные свойства плотности распределения означают, что:
1) вся кривая распределения лежит не ниже оси абсцисс;
2) полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Выясним размерность основных характеристик случайной величины – функции распределения и плотности распределения. Функция распределения 
, как всякая вероятность, есть величина безразмерная. Размерность плотности распределения 
, как видно из формулы (5.4.1), обратна размерности случайной величины.
|
|
|
Пример 1. Функция распределения непрерывной случайной величины Х задана выражением
а) Найти коэффициент а.
б) Найти плотность распределения 
.
в) Найти вероятность попадания величины 
на участок от 0,25 до 0,5.
Решение. а) Так как функция распределения величины непрерывна, то при 
, откуда 
.
б) Плотность распределения величины 
выражается формулой
в) По формуле (5.3.1) имеем:
.
Пример 2. Случайная величина подчинена закону распределения с плотностью:
при 
при 
или 
.
а) Найти коэффициент а.
б) Построить график плотности распределения 
.
в) Найти функцию распределения 
и построить её график.
г) Найти вероятность попадания величины на участок от 0 до 
.
Решение. а) Для определения коэффициента а воспользуемся свойством плотности распределения:
,
откуда 
.
б) График плотности представлен на рис. 5.4.5.
Рис. 5.4.5.
в) По формуле (5.4.4) получаем выражение функции распределения:
График функции 
изображен на рис. 5.4.6.
Рис. 5.4.6.
г) По формуле (5.3.1) имеем:
.
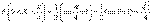Тот же результат, но несколько более сложным путем, можно получить по формуле (5.4.3).
Пример 3. Плотность распределения случайной величины задана формулой:
.
а) Построить график плотности .
б) Найти вероятность того, что величина попадет на участок (-1, +1).
Решение. а) График плотности дан на рис. 5.4.7.
Рис. 5.4.7.
б) По формуле (5.4.3) имеем:
.
24. Вычисление математического ожидания, дисперсии, среднеквадратического отклонения НСВ по ее функции плотности НСВ
Математическое ожидание непрерывной случайной величины вычисляется по формуле:
Дисперсия непрерывной случайной величины вычисляется по формуле:
Среднее квадратическое отклонение непрерывной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:
σ(X) = √D(X)
|
|
|
