 |
Линейное программирование в экономике
|
|
|
|
Линейные методы оптимизации.
Задачи линейного программирования
Термин «линейное программирование» впервые появился в 1951 г. в работах американских ученых (Дж. Данциг, Т. Купманс), а первые исследования по линейному программированию (основные задачи и приложения, критерий оптимальности, экономическая интерпретация, методы решения, геометрическая интерпретация результатов решения) были проведены в конце 30-х годов в СССР в Ленинградском университете Л. В. Канторовичем.
Под линейным программированием понимается линейное планирование, т.е. получение оптимального плана - решения в задачах с линейной структурой.
Линейное программирование широко применяется в сфере военной деятельности, сельском хозяйстве, промышленности, управлении производственными процессами и запасами, в экономике и на транспорте.
Общая постановка задачи линейного программирования.
Общей задачей линейного программирования (ЗЛП) называют задачу: Максимизировать или минимизировать функцию
(1)
при ограничениях: 
(2)
где cj, aij, bi -заданные действительные числа, (1) - целевая функция, (2) - ограничения, 
- план задачи.
Экономическая интерпретация задачи ЛП состоит в следующем. Моделируемая система характеризуется наличием нескольких видов «производственной деятельности» 
, для осуществления которых требуются имеющиеся в ограниченном количестве различные ресурсы 
Расход i-го ресурса на единицу продукта j-го вида производственной деятельности равен aij. В свою очередь при таком потреблении результат j-го вида производственной деятельности для единицы соответствующего продукта (удельная стоимость или прибыль) характеризуется величиной cj.
|
|
|
Цель построения модели состоит в определении уровней (объемов производства) каждого вида производственной деятельности xj, при которых оптимизируется (максимизируется или минимизируется) общий результат производственной деятельности системы в целом без нарушения ограничений, накладываемых на использование ресурсов.
Оптимальным решением (или оптимальным планом) ЗЛП называется решение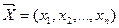 
системы ограничений (2), при котором линейная функция (1) принимает оптимальное значение.
Термины «решение» и «план» - синонимы, однако первый используется чаще, когда речь идет о формальной стороне задачи (ее математическом решении), а второй - о содержательной стороне (экономической интерпретации).
Симметричной формой записи ЗЛП называют задачу
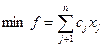
или задачу 
(3)
Линейное программирование в экономике
1. Задача о наилучшем использовании ресурсов. Пусть некоторая производственная единица (цех, завод, фирма и т.д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов, может выпускать n различных видов продукции (товаров) Пj, 
Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т.д.). Все эти виды ограничивающих факторов называют ингредиентами Ri, 
Они ограничены, и их количества равны соответственно b1,b2,...,bm условных единиц. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т.д. Примем в качестве такой меры, например, цену реализации cj, j= 
. Известны также технологические коэффициенты aij, 
, которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции j-го вида. Обозначим через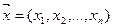 
план производства, показывающий, какие виды товаров П1, П2,..., Пn нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.
|
|
|
Математическая модель задачи имеет следующий вид:
(4)
Так как переменные xj входят в целевую функцию f (
) и систему ограничений только в первой степени, а показатели aij, bi, cj являются постоянными в планируемый период, то (4) - задача линейного программирования.
2. Задача о смесях. В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходных материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе задач относятся задачи формировании минимальной потребительской продовольственной корзины, составлении кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности, смесей для получения бетона в строительстве и т.д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы.
Модель задачи о наилучшем составе смеси рассмотрим на примере задачи формирования минимальной потребительской продовольственной корзины. Задан ассортимент продуктов 
, имеющихся в продаже. Каждый продукт содержит определенное количество питательных веществ, обозначаемые номерами 1,2,..., m (углеводы, белки, жиры, витамины, микроэлементы и др.). Единица j-го продукта содержит aij единиц i-го питательного вещества. Для нормальной жизнедеятельности в заданный промежуток времени нужно потреблять не менее bi единиц i-го питательного вещества. Обозначим через cj стоимость единицы продукта j-го вида. Необходимо определить требуемую потребительскую продовольственную корзину, имеющую минимальную стоимость.
Решение задачи - это количества xj продуктов каждого вида, обеспечивающие необходимое количество питательных веществ при минимальных затратах на исходные продукты.
|
|
|
Математическая модель задачи имеет следующий вид:
(5)
3. Задача о раскрое материалов. Сущность задачи об оптимальном раскрое состоит в разработке таких технологически допустимых планов раскроя, при которых получается необходимый комплект заготовок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму.
На раскрой (распил, обработку) поступает материал нескольких видов в определенном количестве. Из этого материала необходимо изготовить различные изделия. Материал может быть раскроен разными способами. Каждый способ имеет свою себестоимость и позволяет получить разное количество изделий каждого вида. Определить способ раскроя, при котором суммарная себестоимость минимальна.
Пусть n - число различных видов материала, поступающего на раскрой;
dj - количество материала j-го вида, 
m - число различных видов изделий, которые надо изготовить;
bi - число изделий i-го вида, 
; l -число различных способов раскроя;
aijk - число изделий i-го вида, которое можно получить из единицы материала j-го вида при k-м способе раскроя, 
;
cjk - себестоимость раскроя единицы материала j-го вида k-м способом, 
.
Обозначим через xjk - количество единиц материала j-го вида, раскраиваемых k-м способом, .
Математическая модель задачи имеет следующий вид:
.
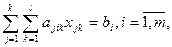
Вместо критерия минимизации себестоимости в задаче может быть взят, например, критерий минимизации отходов. В этом случае в условии должно быть задано количество отходов, получаемых при каждом способе раскроя для единицы материала каждого вида.
|
|
|
