 |
Алгоритм решения СЛАУ в форме жордановых таблиц
|
|
|
|
Рассмотрим исходную СЛАУ в общей форме:

Запишем эту систему в виде нуль - равенств.

Внесем эту систему в жорданову таблицу:
 … …  … … 
| ||
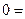
| 
| 
|
| … | … | ……………… |
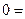
| 
| 
|
| … | … | ……………… |
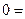
| 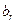
| 
|
Здесь на месте базисных переменных пока стоят нули.
I. Уравнения исходной системы записать в жорданову таблицу в виде нуль - равенств (нуль - строк).
II. Выполнить один шаг жордановых исключений.
1) Принять за разрешающую строку любое нуль-равенство, а за разрешающий столбец любой столбец ( ≠0).
≠0).
2) В новой таблице поменять местами заглавные элементы разрешающей строки и разрешающего столбца (0 и  или
или  и
и 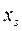 ).
).
3) Выполнить пересчет таблицы. Правила пересчета приведены выше.
4) Вычеркнуть нуль-столбец (элементы разрешающегося столбца можно вообще не вычислять).
III. Проанализировать новую таблицу.
1) Если имеется нуль-строка со всеми нулевыми элементами, кроме свободного члена, то СЛАУ несовместна.
2) Если есть нуль-строки полностью состоящие из нулей, то их надо вычеркнуть.
3) Если нуль-равенства еще имеются, то необходимо вернуться на пункт II.
IV. После ряда шагов жордановых исключений в таблице будет получено общее решение СЛАУ.
 … …  … … 
| ||

| 
| 
|
| … | … | ……………… |

| 
| 
|
| … | … | ……………… |

| 
| 
|
Отметим, что если r= n, то в таблице останется только столбец свободных членов. В этом случае СЛАУ имеет единственное решение.
Примеры решения типовых задач
Пример 1. Решить СЛАУ.
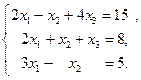
Решение.
Составим жорданову таблицу.
  
| ||
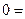
| 2 -1 4 | |
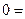
| 2 1 1 | |
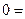
| 3 -1 0 |
Выберем разрешающий элемент. Он выделен жирным шрифтом и подчеркнут.
После пересчета элементов таблица принимает вид:
|
|
|
  
| ||
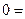
| -17 | -6 -5 -4 |
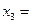
| 2 1 1 | |
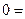
| 3 -1 0 |
Нуль - столбец можно вычеркнуть.
 
| ||
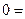
| -17 | -6 -5 |
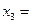
| 2 1 | |
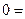
| 3 -1 |
Выберем разрешающий элемент.
После пересчета элементов таблица принимает вид:

| ||
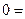
| -42 | -21 |
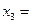
| 5 | |

| -5 | -3 |
Разделим все элементы нуль - строки на -21.

| ||
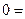
| 1 | |
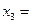
| 5 | |

| -5 | -3 |
Выберем разрешающий элемент.
После пересчета элементов таблица принимает вид:
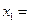
| |
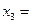
| |

|
Ответ: (2; 1; 3).
Пример 2. Решить СЛАУ.

Решение.
Составим жорданову таблицу.
  
| ||
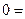
| 2 -3 -1 | |
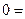
| -1 -1 2 | |
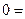
| 1 -4 1 |
Выберем разрешающий элемент.
После пересчета элементов таблица принимает вид:
 
| ||
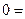
| -4 | 5 -3 |
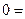
| -5 3 | |

| -4 1 |
Выберем разрешающий элемент.
После пересчета элементов таблица принимает вид:

| ||

| -4/5 | -3/5 |
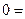
| ||

| -1/5 | -7/5 |
Найдено общее решение СЛАУ в базисе (х 1 ; х 2):

Задания для самостоятельного решения
Решить СЛАУ.
1.

2.

3.
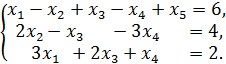
4.

5.
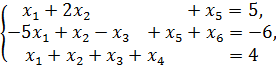
6.

7.

8.

9.

10.

Базисные и опорные решения СЛАУ
Основные понятия
Для отыскания всех базисных решений необходимо:
1) Получить общее решение СЛАУ в любом базисе и выписать первое базисное решение.
2) Выполняя шаг за шагом ряд жордановых исключений переходить от одного базиса к другому и выписывать соответствующие базисные решения.
Чтобы найти все опорные решения СЛАУ можно получить все базисные решения и выбрать из них решения, не содержащие отрицательных элементов. Оказывается, что если наложить определенные условия на выбор разрешающего элемента, то можно найти опорные решения без полного перебора базисных решений, то есть можно переходить от одного опорного решения к другому опорному решению.
|
|
|
Симплексным отношением называется отношение элемента столбца свободных членов к соответствующему элементу разрешающего столбца. В дальнейшем в столбце свободных членов не будет отрицательных элементов и симплексное отношение будет вычисляться только для положительных элементов разрешающего столбца.
|
|
|


