Транспортная задача по критерию времени

Как известно, качество плана транспортной задачи можно оценивать по различным критериям. Рассмотрим здесь в качестве такого критерия (целевой функции) время перевозок.

Транспортная задача по критерию времени возникает при перевозке срочных грузов. Как и в обычной ТЗ, имеется m поставщиков с запасами однородного груза в количестве а_i (i= 1¸ m) и n потребителей, которым этот груз должен быть доставлен в объеме b_j (j= 1¸ n). Требуется составить план перевозок товара так, чтобы удовлетворить потребности при имеющихся запасах и чтобы при этом наибольшее время доставки всех грузов было минимальным.

Пусть Т – матрица времен размера т´п, в которой на позиции (i,j) находится величина t_ij. Тогда задача имеет вид:

z= 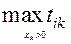→min,

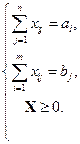(8)

ТЗ по критерию времени не является задачей линейного программирования, т.к. целевая функция z не является линейной функцией переменных х_ij.

Без ограничения общности можно считать, что задача закрытая. В противном случае ее всегда можно закрыть, пропорционально уменьшая избыточные запасы а_i (или потребности b_j) или вводя фиктивные пункты отправления или назначения.

Решение ТЗ по критерию времени может быть получено в следующем порядке. Находится начальный план Х ₀(можно использовать, например, метод северо-западного угла или метод наименьшей стоимости). Определяется значение целевой функции z (Х ₀) = 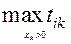= . Все свободные ячейки, которым соответствуют t_ik > , исключаются из рассмотрения (например, закрашиваются темным фоном). Чтобы понизить значение целевой функции, необходимо освободить ячейку (i ₀, k ₀), в которой t_ik достигает максимума. Для этого можно строить так называемые разгрузочные циклы, которые могут включать в свой состав несколько свободных ячеек, т.е. положительные вершины цикла могут опираться на ячейки с нулевыми перевозками. В разгрузочном цикле, начиная с разгружаемой ячейки (i ₀, k ₀), расставляются поочередно знаки «-» и «+» и осуществляют сдвиг на величину q= 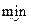t_ik. Если удается эту ячейку разгрузить, то она исключаются из рассмотрения (закрашивается). Получается новый план Х ₁, на котором значение целевой функции не больше, чем на Х ₀. Далее снова пытаются разгрузить ячейку, соответствующую z (Х ₁) = 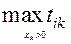= . Процесс продолжается до тех пор, пока возможность разгрузить соответствующую ячейку не исчезнет.

Рассмотрим этот метод на примере.

Пример 6.

Пусть T = 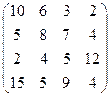, a ₁=20, a ₂=30, a ₃=50, a ₄=50, b ₁=20, b ₂=30, b ₃=40, b ₄=60.

Находим начальный план Х ₀ методом северо-западного угла (итерация 0, рис.1). Базисные нули не записываем. Максимум целевой функции z (Х ₀) = 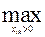{10,8,5,12,4}=12 достигается в ячейке (3,4). Закрасим ячейку (4,1), т.к. время t ₄₁=15 больше, чем z (Х ₀) = 12.

Итерация 0   Вj Аi                       Ө 8   Å 4       Å 4     Ө 12	Для улучшения решения разгрузим ее с по-мощью цикла (3,4)→(2,4)→(2,2)→(3,2). Осуществив сдвиг по циклу, получим новое опорное решение Х1 (итерация 1 на рис.2). Максимум целевой функции на этом опорном решении z (Х1) = 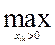{10,8,4,4,5,4}=10 дости-гается в ячейке (1,1). Закрасим ячейку (3,4), т.к. время t 34=12 больше, чем z (Х1) = 10. Разгрузим ячейку (1,1) с помощью цикла (1,1)→(1,2)→(2,2)→(2,1) (итерация 1).

Осуществив сдвиг по циклу, получим новое опорное решение Х ₂ (итерация 2). Максимум целевой функции на этом опорном решении z (Х ₂) = 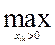{6,5,4,4,5,4}=6 достигается в ячейке (1,2). Закрасим ячейки (1,1), (2,2), (2,3) и (4,3), т.к. в них время t ₁₁=10, t ₂₂=8, t ₂₃=7 и t ₄₃=9 больше, чем z (Х ₂) = 6.

Итерация 1

Итерация 2

Итерация 3

Вj Аi

Вj Аi

Вj Аi

Ө 10

Å 6

Ө 6

Å 3

Å 5

Ө 8

Å 4

Ө 5

Разгрузим ячейку (1,2) с помощью цикла (1,2)→(1,3)→(3,3)→(3,2) (итерация 2). Осуществив сдвиг по циклу, получим новое опорное решение Х ₃ (итерация 3). Максимум целевой функции на этом опорном решении z (Х ₃) = 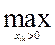{3,5,4,4,5,4}=5 достигается в ячейках (2,1) и (3,3). Закрасим ячейки (1,2) и (4,2), в которых время перевозок не менее t ₂₁=5. С помощью оставшихся не закрашенных ячеек разгрузить ячейки (2,1) и (3,3) не удается, поэтому Х ₃ является оптимальным решением:

Х*=Х ₃= 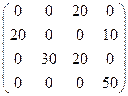, z * =z (Х ₃) = 5.