 |
Укрупненный алгоритм симплексного метода
|
|
|
|
Основная теорема линейного программирования.
Линейная функция, определенная на выпуклом l – мерном многограннике, достигает своего оптимального значения в одной или несколько вершинах этого многогранника.
Если линейная функция достигает оптимального значения в нескольких вершинах, то она имеет это оптимальное значение и в любой точке, являющейся выпуклой линейной комбинацией этих вершин.
Приведенная теорема указывает один из методов решения ЗЛП:
1. найти все опорные планы ЗЛВ;
2. вычислить значения функции цели при каждом опорном плане;
3. выбрать требуемое оптимальное значение и соответствующие опорные планы.
При больших размерностях ЗЛП полный перебор опорных планов практически не возможен. Поэтому обычно применяются методы упорядоченного перебора опорных планов. Рассмотрим самый распространенный универсальный метод решения ЗЛП. Этот метод называется симплексным методом или симплекс – методом.
Симплексный метод состоит в порядочном переходе от одного опорного плана ЗЛП к другому. Переходы осуществляются так, чтобы функция цели всякий раз возрастала. Второе название этого метода – метод последовательного улучшения плана.
Для решения ЗЛП симплексным методом необходимо:
1. привести ЗЛП к канонической форме записи;
2. составить симплексную таблицу для решаемой ЗЛП;
3. найти начальный опорный план ЗЛП;
4. найти оптимальный опорный план ЗЛП.
Для решения ЗЛП используются симплексные таблицы. Эти таблицы отличаются от жордановых таблиц только наличием строки содержащей функцию цели.
1.6.2 Алгоритм отыскания начального опорного плана
Опорный план ЗЛП представляет собой опорное решение системы уравнений – ограничений этой ЗЛП, поэтому алгоритм нахождения начального опорного плана ЗЛП очень похож на алгоритм отыскания опорных решения СЛАУ. Перед отысканием начального опорного плана ЗЛП должна быть приведена к канонической форме записи (система ограничений должна быть системой уравнений).
|
|
|
I. Уравнения системы ограничений записать в симплексную таблицу в виде нуль-равенств с неотрицательными свободными членами.
II. Выполнить одно преобразование таблицы.
1) Принять за разрешающий столбец - столбец, содержащий хотя бы один положительный элемент, не считая свободного члена (f – строка не учитывается).
2) Выбрать разрешающую строку (разрешающий элемент) по минимальному симплексному отношению.
3) В новой таблице поменять местами заглавные элементы разрешающей строки и разрешающего столбца (0 и  или
или  и
и 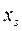 ).
).
4) Выполнить пересчет таблицы, включая f – строку. Правила пересчета приведены выше.
5) Если разрешающая строка содержала нуль-равенство, то нуль-столбец нужно вычеркнуть (элементы разрешающегося столбца можно вообще не вычислять).
III. Проанализировать новую симплексную таблицу.
1) Если имеется нуль-строка со всеми нулевыми элементами, кроме свободного члена, то ЗЛП не имеет допустимых планов.
2) Если есть нуль-строки полностью состоящие из нулей, то их надо вычеркнуть.
3) Если хотя бы один свободный член отрицательный, то допущена ошибка при выборе разрешающего элемента. Необходимо ее устранить.
4) Если имеется нуль-строка в которой все элементы кроме свободного члена меньше либо равны нулю, то ЗЛП не имеет опорных планов.
5) Если нуль-равенства еще имеются, то необходимо вернуться на пункт II.
IV. После ряда преобразований симплексной таблицы в ней будет получен первый опорный план ЗЛП и соответствующая ему функция цели.
1.6.3 Алгоритм отыскания оптимального опорного плана
|
|
|
Перед применением данного алгоритма необходимо найти начальный опорный план и записать его в симплексную таблицу.
I. Если f- строке нет отрицательных элементов, то найденный опорный план оптимален.
1) Ели при этом в f – строке нет нулевых элементов, то оптимальный план единственен. Необходимо выписать ответ.
2) Если среди элементов f - строки имеется l нулевых элементов, необходимо выписать найденный опорный план и выполнить l симплексных преобразований таблицы, то есть получить еще l оптимальных опорных планов. При этом необходимо принимать за разрешающий столбец последовательно все столбцы нулевым элементам f – строки. В этом случае ЗЛП имеет бесчисленное множество оптимальных планов, которые определяются в выпуклой линейной комбинации всех найденных оптимальных опорных планов.
II. Если f - строке есть хотя бы один отрицательный элемент, которому соответствует столбец не положительных элементов, то функции цели не ограничена сверху и ЗЛП решений не имеет.
III. Если в f – строке есть хотя бы один отрицательный элемент и в соответствующем ему столбце есть хотя бы один положительный элемент, то найденный опорный план не оптимален. Необходимо перейти к другому опорному плану.
1) Принять за разрешающий столбец, столбец соответствующий наибольшему по модулю отрицательному элементу f – строки.
2) Выбрать разрешающую строку по минимальному симплексному отношению.
3) Выполнить одно симплексное преобразование таблицы.
4)Перейти на пункт I данного алгоритма.
|
|
|


