 |
Геометрическая интерпретация
|
|
|
|
Геометрическая интерпретация экономических задач дает возможность наглядно представить их структуру и выявить особенности. Графически можно решить только задачи линейного программирования (ЗЛП) с двумя переменными.
Случай двух переменных проясняет свойства ЗЛП, приводит к идее ее решения, делает решения геометрически наглядными.
Пусть дана задача:
f=c1x1+c2x2 
max (8)
(9)
(10)
Рассмотрим геометрическую интерпретацию элементов этой задачи.
Введем на плоскости декартову прямоугольную систему координат x 1 Ox 2и сопоставим каждой паре чисел (x 1 ,x 2) точку плоскости с координатами x 1 и х 2. Выясним сначала, что представляет собой множество точек, соответствующих допустимым решениям данной задачи.
Рассмотрим одно линейное неравенство 
.
Оно определяет на плоскости одну из двух полуплоскостей, на которые прямая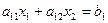 
разбивает плоскость. Найдем, с какой стороны от прямой лежит полуплоскость, точки которой удовлетворяют заданному неравенству. Это можно сделать путем подстановки координат одной точки в неравенство. Если координаты точки удовлетворяют неравенству, то эта точка лежит в полуплоскости, соответствующей решению данного неравенства. Штриховку прямой надо произвести так, чтобы она «закрывала» выбранную точку. В противном случае неравенству соответствует другая плоскость.
Каждое из ограничений (9), (10) задает на плоскости х 1 Oх 2 некоторую полуплоскость. Допустимое множество планов ЗЛП геометрически изображается пересечением (общей частью) полуплоскостей, определяемых отдельными ограничениями. Полуплоскость - выпуклое множество. Множество называется выпуклым, если ему вместе с двумя произвольными точками принадлежит и прямолинейный отрезок, их соединяющий. Пересечение любого числа выпуклых множеств является выпуклым множеством. Таким образом, область допустимых планов задачи (8) - (10) есть выпуклое множество. На рисунке 1 представлены некоторые ситуации, когда область допустимых решений ЗЛП - выпуклый многоугольник (а), неограниченная выпуклая многоугольная область (б), единственная точка (в), прямая линия (г), луч (д), отрезок (е), пустое множество (ж).
|
|
|
X2 
X2 X2
 |
 |
б)
0 а) X1 0 X1
Х2 Х2 Х2
 | |||||
 | |||||
 | |||||
в) 1 д)
г)
0 Х1 0 Х1 0 Х 1
Х2 Х2
 | |||
 | |||
е) ж)
Х1
|
Рисунок 1
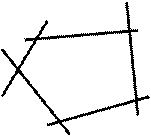
Перейдем к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП многоугольник ABCDE (рисунок 2).
X2
B C
M
A
D
E
N
0 X1
Рисунок 2
Выберем произвольное значение целевой функции f = f 0, например f 0 =0. Получим c 1 x 1+ c 2 x 2= f 0 . Это уравнение прямой линии MN. В точках прямой MN целевая функция сохраняет одно и то же постоянное значение f 0.
Считая f 0 параметром, получим семейство параллельных прямых, называемых линиями уровня целевой функции. Нас интересуют те точки области допустимых решений, которые принадлежат линии уровня с наибольшим (наименьшим) значением f 0 по сравнению с его значениями для всех других линий уровня, пересекающихся с областью допустимых решений.
Рассмотри частные производные функции цели по переменным x1 и х2, то есть по направлению осей координат:
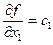(11)
(12)
Каждая частная производная функции показывает скорость ее возрастания вдоль соответствующей оси. Следовательно, с 1 и с 2 - скорости возрастания вдоль осей Oх1 и Oх2. Вектор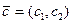 
является градиентом функции. Он показывает направление наискорейшего возрастания целевой функции, вектор
|
|
|
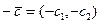указывает направление наискорейшего убывания целевой функции. Вектор 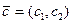перпендикулярен к прямым семейства: 
|
|
|
