Алфавит. Слово. Язык. Информация.

Так как наш курс математический, то мы будем опираться на недоказуемое утверждение (тезис), которое используется математиками при изучении информации.

Тезис. Любая информация может быть представлена словом в конечном алфавите.

Заметим при этом, что не любое слово в конечном алфавите является информацией.

Опр. Алфавит A – это конечный или бесконечный набор символов: A={a₁,a₂,…,a_n,…}.

Опр. Слово – это конечный упорядоченный набор символов алфавита.

Выделяется специальное пустое слово (слово, не содержащее символов).

Пусть 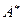– множество всех слов в алфавите .

Опр. Язык L – это подмножество . ().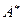

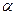
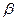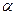Опр. Конкатенация слов и .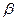

 

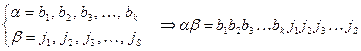
Информация (слово в конечном алфавите)- нематериальная сущность. При любых действиях с информацией необходимо различать собственно информацию (слово) и материальный носитель, с помощью которого производится действие с информацией: книга, дискета, электромагнитное поле и т.п.

Назовем информационным объектом материальный носитель с находящейся на нем информацией. Структура материального носителя может быть сложной. Например, он, как целое, может состоять из частей, с каждой из которых может быть связан свой собственный информационный объект. Или наоборот, из нескольких ИО может быть сформирован новый ИО, как целое из частей. Из этих новых ИО формируются еще более сложные системы ИО и т.д. Для таких «сложных» ИО обычно используется термин информационная система (ИС).

 

Информация и алгоритм.

Задачи, алгоритмы

В любой математической дисциплине, которая претендует на наличие собственного взгляда на "математическую" проблематику, исходные понятия не определяются математическим языком. Обычно, речь идет об "интуитивных" объектах, сущность которых может обсуждаться за пределами математики.

В этом курсе мы тоже будем иметь дело с несколькими лишь интуитивно определяемыми понятиями. Важнейшие из них - задача и алгоритм. Сразу оговорим очевидное. Для описания базовых понятий раздела науки используются те же слова, которые применяются и на бытовом уровне. Но в науке они становятся терминами и приобретают особый смысл. В лекции иногда трудно избежать ситуации, когда одно и то же слово используется и в качестве термина, и в качестве обиходного. В тексте при подозрении на двусмысленное понимание для терминов будет использоваться курсив, а для обиходных – кавычки, а там, где двусмысленность при разумном понимании невозможна – обычный шрифт.

Задача

Начнем с обсуждения первого из упомянутых понятий – понятия задача. При описании базовых понятий или аксиоматики используется три способа: аналогия, пример и расчленение «менее элементарных» сущностей на совокупность «более элементарных. Пойдем и мы по этому пути.

Наш курс тесно связан с двумя математическими дисциплинами: математической логикой и дискретной математикой. Поэтому самая простая идентификация понятия может быть дана по аналогии. Вспомним то, что имелось в виду под задачей в этих дисциплинах. В нашем курсе мы будем иметь дело примерно с тем же самым.

Например, в [1] определение задачи вообще не дается, считается, что оно «интуитивно очевидно». В [2] под задачей понимается «некоторый общий вопрос, на который следует дать ответ». При этом «задача содержит несколько параметров или свободных переменных, конкретные значения которых не определены».

В [4] под задачей понимается «выбор наилучшей конфигурации или множества параметров для достижения некоторой цели». При этом задачи делятся на непрерывные и комбинаторные. «В непрерывных задачах обычно отыскивается множество действительных чисел или даже некоторая функция; в комбинаторных задачах – некоторый объект из конечного или возможно бесконечного счетного множества». Другими словами, задача оптимизации – это пара (F,c), где F – произвольное множество, область допустимых точек, а – c функция стоимости, отображающая элементы F на множество действительных чисел. Требуется найти такую x* точку из F, на которой значение функции c (x*) обладает определенным свойством, например, минимально, максимально и пр.

Теперь займемся «расчленением» сущностей, приведенных выше. Задачи, рассматриваемые в нашем курсе, это, в подавляющем большинстве, задачи комбинаторные или дискретные. Уже само слово комбинаторный относится к упомянутому выше множеству F. Вернее, к способу его задания. Мы видим, что при таком задании с задачей обычно связывается два объекта: множество параметров и структура связей между ними. Параметры – «язык» для описания условий задачи. Структура связей содержит нечто, позволяющее описать F, а также сформулировать вопрос (см. [2]) или требование к c (x*) трактуемое как вопрос, свойство функционала и пр. (См. [4]).

В теории сложности термин задача сразу же разбивается на два термина: индивидуальная задача и массовая задача. Это связаны со способом задания параметров. Массовая задача предполагает описание множества параметров, а индивидуальная задача возникает, при фиксации значений этих параметров.

Понятие формы задачи, грубо говоря, возникает в связи с возможностью "незначительно" модифицировать вышеупомянутые форму вопроса или свойство c (x*).

Поясним сказанное на примерах. Но эти примеры будут носить не только иллюстративный характер. В их тексте мы дадим и разъясним многие общие (выходящие за рамки примера) понятия, которые в дальнейшем будут использоваться.

Многие из этих примеров будут неоднократно использоваться в дальнейшем, поэтому для упрощения ссылок на них мы дадим приведенным ниже задачам краткие названия.

 

Пример 1. (Поиск максимального числа). Заданы N целых чисел: a₁,…a_N. Требуется найти максимальное из них.

На примере этой простейшей задачи постараемся подробно проанализировать условие задачи.

Здесь параметрами являются числа: N и a₁,…,a_N. Правильнее представлять их в виде объектов, имеющих числовые значения. Это означает, что количество сущностей, между которыми при формулировке и решении задачи будут устанавливаться связи, равно 2N+2. Одна сущность предназначена для описания мощности множества сравниваемых чисел, другая – представляет собой числовое значение этой мощности (оно равно N), N сущностей предназначено для идентификации сравниваемых объектов. Эта идентификация достигается путем индексации: 1,…,N. Остальные N: a₁,…a_N – это веса (значения) проиндексированных объектов. В дальнейшем для сущностей, принимающих числовые значения, будем использовать понятие параметр, а для остальных – объект. Они не равноправны: сначала должны быть заданы объекты, а затем уже – параметры. Это означает, что задание параметра возможно после задания объекта. Можно также задать все объекты и лишь часть параметров или задать часть объектов, а затем определить параметры, с ними связанные.

В нашем примере связи на множестве объектов строятся через их параметризацию с использованием отношения сравнения чисел. Задание (свойство c (x*))в данном случае состоит в нахождении объекта, значение которого максимально. Если всем этим объектам и параметрам присвоены конкретные значения, то получается индивидуальная задача. В ситуации, когда речь идет о произвольных значениях объектов, мы имеем дело с массовой задачей. Заметим, что роли параметра N и параметров a₁,…a_N неодинаковы, т.е. можно говорить о множествах индивидуальных задач, получаемых из массовой задачи путем фиксации параметра N.

Уже такая простейшая задача позволяет проиллюстрировать понятие формы задачи. В данном случае можно говорить о задаче в форме оптимизации. Подобная форма возникает тогда, когда речь идет об экстремуме некоторого функционала на множестве исходных параметров задачи.

Задача в вычислительной форме получается при следующей модификации вопроса: "Требуется найти величину максимального из данных чисел". То есть здесь не нужно указывать сам объект, а только его числовое значение. Казалось бы, это условие не очень важное, но для ряда задач трудности решения их в оптимизационной и вычислительной формах различаются весьма существенно.

Другой распространенный тип задач - задачи в форме распознавания. В нашем случае для подобных задач добавляется еще один параметр B, а задание выглядит следующим образом. Требуется ответ на вопрос, существует ли среди объектов a₁,…a_N такой, значение которого не меньше, чем B? При этом, вообще говоря, не требуется ни указывать сам объект, ни его значение.

В последнем случае мы видим, что речь идет не только о форме задания, но и изменении множества параметров. То есть задача уже другая, но "близкая" к исходной. Это соответствует интуитивному представлению о том, что «незначительное» изменение в формулировке условия может приводить к «незначительному» изменению самой задачи.

Что значит незначительно? Как при этом меняется трудность решения? Этими вопросами мы тоже будем заниматься в нашем курсе.

 

Пример 2. (Разложение на множители). Дано натуральное число N. Требуется разложить его на простые множители.

Параметром здесь является само число (значение объекта). При его фиксировании возникает индивидуальная задача. Если говорить о форме задачи, то она явно не оптимизационная, да и вычислительной не является, хотя в широком смысле под вычислением в данной задаче можно понимать нахождение всех простых делителей с их кратностями. Близкая к данной задача в форме распознавания состоит в определении простоты числа (задача о простоте числа).

Пример 3. (Задача о камнях или Задача о разбиении). Даны: число B, число N и числа (объекты с числовыми значениями) a₁,…a_N. Требуется разбить все объекты на две части так, чтобы суммы значений объектов в каждой части были одинаковы.

С некоторой натяжкой такую форму можно считать оптимизационной, если под оптимумом (свойством c (x*)) понимать нахождение набора суммарного веса (S a_i)/2).Определение существования такого разбиения приводит к задаче в форме распознавания.

Пример 4. (Задача о гамильтоновом цикле). Дан простой неориентированный граф G c N вершинами. Требуется узнать, существует ли в нем гамильтонов цикл. (Гамильтоновым называется цикл в графе, который проходит через каждую вершину графа ровно по одному разу.)

Набор исходных параметров - это число N и множество ребер графа, задаваемых как пары разных чисел из множества 1,…,N. Понятие гамильтонова цикла задает связь на множестве параметров.

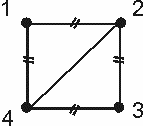
На рисунке приведен пример графа с N=4, в котором отмечены ребра, входящие в гамильтоновы циклы. Их два, в одном последовательно обходятся вершины с номерами: 1-2-3-4-1, в другом – 1-4-3-2-1.

Задача представлена в форме распознавания. Вычислительную и оптимизационную форму здесь искать малоинтересно. Но возникает еще одна форма - перечислительная. В этой задаче требуется найти число различных гамильтоновых циклов графа.

В дальнейшем будем, как правило, называть эту задачу просто: " гамильтонов цикл ".

Пример 5. (Задача о коммивояжере.) Дан граф G c N вершинами, ребрам которого приписаны веса c_ij. Требуется найти гамильтонов цикл экстремальной длины. (Длина гамильтонова цикла может задаваться по-разному. В большинстве случаев – это сумма длин входящих в цикл ребер. Если не оговаривается обратное, то именно эта ситуация и имеется в виду. Но за длину можно брать и максимальный (минимальный) вес входящего в него ребра, и более сложный функционал от длин ребер. Наиболее распространенный случай, когда под экстремумом понимается минимум. Если же экстремум трактуется как максимум, то это оговаривается отдельно. Такие задачи называются задачами коммивояжера на максимум).

Можно считать, что граф полный (отсутствующим ребрам приписать специальным образом выбранные «большие» значения). Тогда набор исходных параметров определяется числом N и матрицей весов ребер С=||c_ij||. Индивидуальная задача получается из массовой фиксированием этих параметров.

В дальнейшем будем называть эту задачу просто " коммивояжер ".

В формулировку задания входит понятие гамильтонова цикла, которое и задает связь на множестве параметров.

В вышеупомянутом варианте мы имеем задачу в форме оптимизации. Вычислительный вариант задачи состоит, например, в нахождении длины минимального гамильтонова цикла. В случае задачи на минимум в варианте распознавания задается еще число B и требуется ответить на вопрос, существует ли гамильтонов циклы с длиной, не превосходящей B.

Можно получить еще один вариант - перечислительный. Он состоит в нахождении количества минимальных гамильтоновых циклов.

Приближенный вариант без оценки точности состоит в нахождении гамильтонова цикла, который отличается от минимального "незначительно". При этом в понятие «незначительно» никакого формального смысла не вкладывается.

Приближенный вариант с оценкой точности может выглядеть следующим образом. Требуется для заданного числа k найти гамильтонов цикл, превосходящий минимальный не более чем в k раз.

 

Пример 6. (Задача о выполнимости КНФ.) Задана булевская функция F от N переменных в виде конъюнктивной нормальной формы K. Требуется определить, существует ли такой набор значений переменных, на котором функция обращается в единицу.

Здесь мы имеем задачу в форме распознавания. Исходными параметрами являются N и K. Что касается задания связей на множестве исходных параметров, то их можно проиллюстрировать следующим образом. Всех конъюнкций от N переменных 3^N. Обозначим это множество через Q(N). Индивидуальная задача получается из массовой путем фиксирования числа N и подмножества M из Q(N).

В дальнейшем будем называть эту задачу просто " КНФ-выполнимость ".

Пример 7. (Задача о рюкзаке.) Дано N объектов и число B. Каждому объекту приписаны два числа. Первое назовем ценой, а второе весом объекта. Требуется выбрать такое подмножество объектов, чтобы их суммарный вес не превосходил B, а совокупная цена была максимальной.

Мы имеем N+2N параметров, задание которых определяет индивидуальную задачу. Задача представлена в оптимизационной форме. Используя вышесказанное, легко получить как вычислительную, так и форму распознавания.

В дальнейшем будем называть эту задачу просто " рюкзак ".

С помощью этих примеров мы уже проиллюстрировали почти все необходимое, но все же мы кратко упомянем еще несколько задач, которые понадобятся нам в дальнейшем.

Задача о клике (" клика ") состоит в нахождении максимального (по числу вершин) полного подграфа K заданного графа G. Задача о кратчайшем остове (" остов ") состоит в нахождении минимального (например, по сумме длин входящих ребер) остовного дерева T графа G, ребрам которого приписаны веса. Само название Задача о кратчайшем пути (" кратчайший путь ") между двумя фиксированными вершинами графа уже все определяет. Задача об изоморфизме графов (" изоморфизм графов ") состоит в определении изоморфизма пары заданных графов.

 

Алгоритм

Если с понятием задачи все теперь более или менее понятно, то вот с понятием алгоритма дело обстоит сложнее. Работа в этом направлении породила не только теорию сложности или столь распространенные сейчас компьютеры, но и разделение математики, в которой на некоторое время остро стал вопрос о конструктивности. Но это тема отдельного большого разговора.

Итак, есть задача. Встает вопрос о ее решении. Какую бы форму задачи мы не взяли, решение задачи предполагает нахождение некоторого объекта. В случае индивидуальной задачи по исходному набору параметров (объектов и их значений) требуется найти некоторый объект (если речь идет об оптимизационной форме), число (если речь идет о вычислительной или перечислительной форме), вариант (один из двух: "да" или "нет", если речь идет о задаче в форме распознавания).

В жизни мы отнюдь не всегда для решения задач используем "алгоритмы". (Скорее, почти никогда их не используем). Действительно, мы можем найти объект, угадав его или используя наш опыт.

В этих случаях процесс нахождения состоит из двух важных этапов. Сначала в результате угадывания или опыта мы в качестве предполагаемого решения выбираем некоторый объект. Затем мы убеждаемся, что данный объект является требуемым решением задачи. Назовем первый этап этапом предложения, а второй - этапом проверки.

Если мы имеем задачу в форме распознавания, то нам не важна "логика" действий на первом этапе. Действительно, мы просто строго проверяем объект на наличие требуемого свойства. Например, в задаче о камнях мы считаем сумму весов предложенного подмножества объектов, в задаче о гамильтоновом цикле проверяем предложенное подмножество ребер на "гамильтоновость".

В том случае, когда правильное предложение возникает в результате отгадки, интуиции, опыта и пр., принято объединять все эти процессы, вводя понятие оракула. То есть оракул - это абстрактная сущность, которая мгновенно, без усилий способна предоставить предложение, не нуждающееся в проверке. Конечно, его можно проверить, но оракул на то и оракул, чтобы не ошибаться.

Для задач в форме оптимизации тоже может иметь место этап предложения, но этап проверки эквивалентен исходной задаче. В жизни мы можем его заменить верой или интуицией, но в математике требуется нечто иное. Требуется процедура, не зависящая от производящего ее субъекта, которая бы абсолютно достоверно позволяла находить (проверять) требуемый в условии задачи объект.

Это и есть интуитивное представление алгоритма. В [2] например, оно звучит так. Алгоритм - это общая, выполняемая шаг за шагом процедура решения задачи. Прилагательное "общая" отвечает за автоматизм, независимость от субъекта, использующего алгоритм. Требование выполнения работы "шаг за шагом" здесь не ограничивает тип алгоритма (например, не отбрасывает параллельные или вероятностные алгоритмы), а лишь указывает на предсказуемость и проверяемость самой процедуры решения.

Во многих попытках дать определение алгоритма используются понятия "искусство" и "автоматизм" (машинное исполнение). При этом первое как раз должно отсутствовать в этом самом "алгоритме", а второе должно его характеризовать.

Формализация понятия "алгоритм" необходима также из-за "несимметричности" ответа на вопрос, существует ли алгоритм для решения задачи Z?

Действительно, ответ "да" может быть получен путем построения некоторой процедуры решения, которая укладывается в "интуитивное" понятие алгоритма. Такие процедуры и строились в процессе всей истории математики, когда формальным построениям самого понятия алгоритм внимания не уделялось. Если для некоторой задачи не могли построить метода решения, то это списывалось на недостаток умения.

Имея лишь интуитивное представление об алгоритме, нельзя доказать, что этого самого алгоритма не существует.

В 30-е годы стали появляться первые формальные схемы алгоритма. Эти схемы были предназначены исключительно для теоретических исследований. С некоторыми из них мы познакомимся здесь. Речь пойдет, например, о машинах Тьюринга (МТ), нормальных алгорифмах Маркова (НАМ) и др.

Алгоритм производит некоторые "действия" с объектами и параметрами, начиная с исходных условий задачи (входные условия, вход). Во всех известных формальных схемах этот вход как-то задается. В самом общем случае можно считать, что это задание выглядит в виде слова в некотором алфавите.

Множество (конечное или бесконечное) символов назовем алфавитом A. Словом P в алфавите A назовем любую конечную последовательность символов алфавита.

Если множество символов одного алфавита является подмножеством символов другого, то первый называется подалфавитом второго. А второй - надалфавитом первого.

Пусть A - подалфавит некоторого алфавита B. Слово, состоящее из символов алфавита A, будем называть словом в алфавите A. Слово, состоящее из символов алфавита B, будем называть словом над алфавитом A.

Заметим, что достаточно ограничиться алфавитом из двух символов, например, 0 и 1. Любой символ a_i алфавита A={a₁,…,a_n,…} может быть закодирован следующим образом: a_i =011...10, где 1 повторяется n раз.

В известных формальных схемах (формализмах) "алгоритм" можно представить как некоторое пошаговое преобразование одних слова в другие, начиная с входа x₁,…,x_n = X. В результате последнего шага таких преобразований получаем некоторое выходное слово Y. Его можно трактовать как результат работы алгоритма. Задавая буквы входного алфавита числовыми последовательностями, можно считать, что речь идет о вычислении функции f(x₁,…,x_n)=f(X)=Y.

Обратим внимание на употребление понятия эквивалентности в связи с наличием нескольких возможных представлений (кодировок, способов записи) входных объектов.

Два выражения (кодировки) B и C считаются эквивалентными B»C в двух случаях: либо оба выражения не определены (бессмысленны), либо определены и обозначают один и тот же объект.

Будем говорить, что алгоритм Á является алгоритмом в алфавите A, если он переводит слова x₁,…,x_n в алфавите A в слова f(x₁,…,x_n) в алфавите A.

Будем говорить, что алгоритм Á является алгоритмом над алфавитом A, если он переводит слова x₁,…,x_n над алфавитом A в слова f(x₁,…,x_n) над алфавитом A.

При этом алгоритмÁ может работать не с любыми словами алфавита. Множество тех слов, к которым он применим, назовем областью действия алгоритма Á, а результат применения алгоритма Á к слову P обозначим через Á (P). При этом сам алгоритм не обязан распознавать слова из своей области действия.

Рассмотрим два алгоритма Á и Â над алфавитом A.

Если Á(P)»Â(P) для любого слова P в алфавите A, то эти алгоритмы называются вполне эквивалентными относительно A.

Если Á(P)»Â(P) для любого слова P в алфавите A такого, что хотя бы одно из выражений Á(P) или Â(P) определено и является словом в алфавите A, то эти алгоритмы называются эквивалентными относительно A.

Рассматриваемые ниже формальные подходы к понятию алгоритма заслужили внимание благодаря гипотезам типа тезиса Черча.

Этот тезис говорит об эквивалентности широкого неформально и смутного понятия "интуитивный алгоритм" узкому и весьма замысловатому на первый взгляд формализму типа алгорифма Маркова (МТ) или машины Тьюринга. Утверждается, что для любой задачи, для которой существует «интуитивный» алгоритм решения, можно, например, построить МТ, которая будет решать эту задачу.

Рассмотрим теперь данные формализмы подробно. Заметим, что алгоритм может предназначаться как для решения массовой, так и для решения индивидуальной задачи. (Например, алгоритм сложения двух чисел и алгоритм сложения 5 и 2). Конечно, мы изначально предполагаем, что алгоритм должен решать массовую задачу.

Сделаем одно замечание. Во всех перечисленных ниже формальных подходах алгоритм имеет дело с преобразованием одних слов в другие. То есть, условие задачи Z можно рассматривать как слово в некотором алфавите A. Обозначим все множество слов этого алфавита через A*. Подмножество слов алфавита назовем языком. Обратим внимание, что в содержательном смысле не все слова алфавита являются условиями индивидуальных задач из Z.

Особенно удобно ставить некоторый язык из A* в соответствие задачам в форме распознавания. В этих задачах в качестве решения возможно два варианта: 1 ("да") или 0 ("нет"). Таким образом, задаче Z в форме распознавания можно сопоставить язык L_Z, содержащий в качестве слов все слова из A*, которые являются условиями индивидуальных задач с ответом "да".

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: