 |
Теорема (граница Хемминга)
|
|
|
|
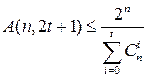
Доказательство:
Пусть V – наш код, V’ – шар радиуса t, тогда в это шаре расстояние между двумя любыми точками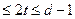 
.
Таких множеств // 
// 
.
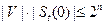По определению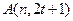 
и получим искомое неравенство.
Теорема (граница Джоши)
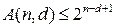
Доказательство:
Пусть V – код с расстоянием d, 
, V’ – множество всех векторов, у которых 
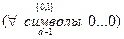. Тогда 
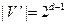, для любых x, y 
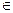V’: 
.
.
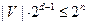Теперь получим оценку снизу.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
Теорема (Варшамова-Гильберта)
Доказательство:
Построим код V* следующим образом:
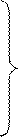Итерации:
1) x 1 → V*
2) x 2 → V* \ St (x’)
… p- 1 точка кода.
p) xp → V* \ 
В какой-то момент сделать это не сумеем. Расстояние между любыми точками таким образом построенного кода равняется 2 t, откуда и следует неравенство.
Теорема (Плоткина)
Доказательство:
Рассмотрим код 
. Построим таблицу.
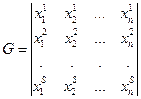
k 1 k 2 k n – количество единиц в каждом столбце.
Рассмотрим сумму расстояний между всеми кодовыми словами.
Здесь каждое расстояние подсчитано 2 раза. Тогда 
.
max x (S-x) достигается при x = S /2. Воспользуемся этим.
(
)
Хотим, чтобы 
. Поставим это неравенство в ():
Теорема Шеннона для канала с шумом.
Факты из теории вероятности.
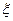- случайная величина.
- мат. ожидание.
- дисперсия.
Теорема (неравенство Чебышева)
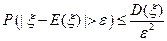
Испытание Бернулли, вероятность успеха p (неудача 1- p). Есть n испытаний. Тогда 
.
Доказательство:
Схема кодирования и декодирования. Вспомогательные утверждения.
Если передается слово из n 0 и 1, то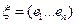 
- вектор, подчиняется распределению Бернулли 
мат. ожидание и дисперсия такого вектора считаются по доказанному выше.
|
|
|
1) Есть код C = { x 1… xm } – кодовые слова
2) Применяем декодирование в ближайшее слово (по наибольшему правдоподобию)
ПередачаПрием
a x 1 T(C) – таблица
b x 2 
… …
… xM
3) Вероятность ошибки декодирования
P (x) – вероятность неправильного декодирования x 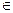* Bn. ∑ P (x) – зависит от комбинаторных свойств кода, ошибки p, потерь в канале и т.д.
Pc (характеристика кода C) = 1\ M ∑ P (x)
Число различных кодов в Bn: 
*формула* - число кодов мощности M в Bn.
Пусть L – множество таких кодов. ρ (x) – вероятность правильного декодирования.
ρс = 1\ M ∑ ρ (x)
Pc + ρс = 1
P *(M, n, p) = min Pc → P *(M, n, p) ≤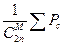 
, где P *(M, n, p) – характеристика существующего кода, являющаяся наилучшей из возможных с точки зрения ошибки декодирования.
На сегодняшний день наилучший код не найден, все существующие отличны от него в константу раз.
Лемма (): Возьмем точку в Bn и шар S[pn] (x), оценим число точек в нем: | S[pn] (x)| ≤ 2nH ( p )
Доказательство: | S[pn] (x)| =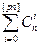 
Вспомним, что 0 ≤ p < 1\2, принцип – декодирование в ближайшее, (1 – p)n ≥ p(1 – p)n-1 ≥ … ≥ pk(1-p)n-k
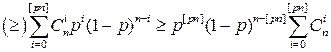, где 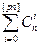- мощность.
Тогда | S [ pn ](x)| ≤ (p [ pn ] (1 – p) n – [ pn ])-1 =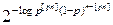 
= 2 nH ( p )
xi → канал → Y
Считаем, что Y = x i + e, e – вектор ошибок
τ – случайная величина = | e | (количество ошибок)
Т.к. источник Бернулли, то E (τ) = np, D (τ) = np (1 – p)
b =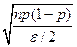 
- добавим к мат ожиданию, тогда радиус шара *формула*
Лемма (
): P { τ > ρ } ≤ ε \2 для любого заранее заданного ε.
Доказательство: Применим неравенство Чебышева:
P {| τ – E (τ)| > ε } ≤ D (τ)\ ε 2
ρ = [ E (τ) + b]
P {| τ – nP | > b} ≤ D (τ) \ b 2
P {| τ – nP | > b } ≤ ε \2
P (τ > ρ) = P {| τ – nP | > b } – проверим это:
 |
- τ np τ
τ > nP + b
τ – nP > b
Лемма (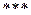
): Пусть ρ = [ E (τ) + b ] и b = формула, тогда 1\ n log | Sρ (x)| ≤ H(P) – O(n -1\2) при n → ∞.
Доказательство: Из леммы () и леммы ():
| Sρ (x)| ≤ 2 nH (ρ \ n ). Домножим на log и поделим на n.
|
|
|
1\ n log | Sρ (x)| ≤ H(ρ \ n) = - ρ \ n log ρ \ n – (1 – ρ \ n) log (1 – ρ \ n) = - [ nP + b ]\ n log [ nP + b ]\ n – (1 – [ nP + b ]\ n ] log (1 – [ nP + b ]\ n) ≈ - P log P – (1 – P) log (1 – P) – O(b \ n) = O(n -1\2)
(1) 
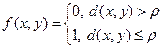
(2) 
Вероятностное доказательство теоремы.
Теорема Шеннона: для любого R: 0 < R < C (ρ) P *(M, n, P) → 0, n → ∞
Доказательство: Пусть передаем x i, принято некое y, оцениваем ошибку декодирования. Ошибочное декодирование:
 | |||||
 | |||||
 | |||||
|
|
Ближе, чем x i ни одной точки к y нет y декодируется в x i.
Кодовые точки упали как угодно, на них строим шар радиуса ρ.
Декодируем так: если точка у попала в шарик радиуса ρ вокруг кодовой точки, то декодируем ее в данную кодовую точку, если в этом шаре нет других точек; если есть, то у декодируем в произвольно заданную точку. Это будет ошибкой. Вводим функцию (1), тогда вероятность ошибки оценивается суммой (2)
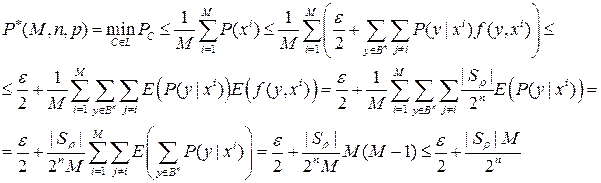
Применяем лемму (): Rn = log M, M = 2 Rn
1\ n log (P *(M, n, P) – ε \2) ≤ 1\ n log | Sρ | M \2 n = 1\ n log | Sρ |2 Rn - n ≤ R – C (ρ) – 1 – O(n -1\2) + 1 → P *(M, n, P) < ε \2 + 2- δn. Теорема доказана.
|
|
|
