Наиболее распространенные способы кодирования и их свойства. Алгоритмы кодирования.

В этом разделе мы будем рассматривать просто кодировки. (То есть такие, когда одно слово представляется в виде другого слова).

Во всех случаях рассматривается следующая модель. Есть два алфавита

А = (а ₁, …, а_n) и B = (b ₁, …, b_q).

Кодирование φ это отображение слов α в алфавите А в слова β=φ(α) в алфавите В.

Кодирование называется дешифруемым, если по слову β однозначно восстанавливается α. (Отображение φ – биекция).

Кодирование слов и поиск минимального кода

Пусть у нас есть коды объектов - слова в алфавите A.

Опр. Длина кода – количество символов в нем.

Нельзя ли построить код минимальной длины, пусть даже в другом алфавите B?

Оказывается, эта задача алгоритмически неразрешима.

Теорема: Не существует МТ, которая строит код минимальной длины.

Доказательство: Упорядочим B_n (по длине в лексикографическом порядке):

0, 1, 00, 01, 11, 000, 001… (*)

Пусть есть МТ Т 1, который умеет на х строить К (х) минимальной длины (по К (х) можем однозначно восстановить х). Строим Т 2 = F (T 1, …). Натуральное m, T 2 в (*) слева направо подходит первое x: K (x) ≥m. Следовательно, m – код х (длина m→ log m), но K (x) – лучше по длине. Значит, K (x) ≤ log m.

Признаковое кодирование.

 

Признаки:

 

 

Рассматривается множество объектов s₁,…,s_m (люди, болезни, месторождения и т.п.), которое нужно кодировать, т.е. каждому объекту нужно сопоставить слово в алфавите. При этом есть другое множество объектов, называемых признаками, которые мы умеем кодировать. Тогда кодом объекта при признаковом кодировании является вектор, компонентами которого являются коды (значения) признаков, применительно к данному объекту.

Например,

α (s_i) = (α ₁, …, α_k)

Пример: s ₁ … s_n – люди.

1) Цвет волос

2) Рост

3) Вес

p ₁ … p_n – размер частей тела человека.

Следующий шаг – появление классов объектов, задача – определить, какие из объектов к каким классам принадлежат.

В случае бинарных значений признаков при признаковом кодировании объектом исследования является матрица вектров признаков.

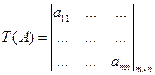
Выше мы уже говорили о стремлении строить неизбыточные коды. С этой задачей связана известная проблема дискретной математики – проблема поиска минимальных тестов таблицы.

Опр. Тест - это множество столбцов в T (A) такое, что все строки в подматрице, образованной этим множеством, попарно различны.

Длина теста – количество столбцов в тесте.

Минимальный тест – тест с минимальным количеством столбцов.

Признаковое кодирование и проблема распознавания.

С признаковым кодированием тесно связана проблема отнесения объекта к определенному классу.

Есть классы объектов. Субъекты определенным образом кодируют эти объекты в некотором признаковом пространстве.

 

x = (x ₁ ,…,x_n)

	Признаковое пр-во

 

Выборка известных кодированных объектов из класса называется обучающей выборкой.

Задача: Взяв объект неизвестного класса, сопоставить ему набор признаков x, отнести его к какому-либо классу, по возможности однозначно.

 

х

 

Если между информационным объектом и кодом связи нет, то задача не решаема. В противном случае все зависит от нас.

Гипотеза компактности:

1) 2 точки пространства x, принадлежащие одному классу, могут быть соединены непрерывной кривой, все точки которой принадлежат этому классу.

2) Если точка принадлежит классу k, то в некоторой ненулевой окрестности почти все точки принадлежат к классу k.

3) Число неопределенных точек пространства x имеет меру 0.

Приведем примеры некоторых методов распознавания.

Метод разделяющих функций

Классы k ₁ (×) и k ₂ (○) – обучающие выборки.

 

 

Это в чистом виде эвристический подход. Строим функцию по обучающей выборке, затем относительно нее определяем, к какому классу относить новые точки.

4.2.3.2 Метод комитетов

 

Комитеты (эксперты)

 

Всегда существует комитет такой, что для любой точки из обучающей выборки

x: M = (p_{i 1} ,…,p_ik), k >

p_{i 1} ,…p_ik – корректно определяют точку x.

Если больше половины правильно классифицируют эту точку, то это называется комитет.

x₀ (конкретная точка) ← p ₁ ,…,p_s (по большинству относятся к k ₁ или k ₂) _.

4.2.3.3 Метод потенциалов (пришел из физики)

x • ← заряд (ассоциируем каждую точку с неким зарядом).

U(X) – потенциальная функция поля.

 

Вычисляем потенциал x₀, и смотрим, к чему он ближе.

Метод вычисления оценок

k ₁ и k ₂ – строится обучающая таблица.

k2

k1

X = Bⁿ (0,1)

1) В этой таблице строятся опорные множества T ₁ ,…T_k.

Tj {1 ,…,n } – подмножества столбцов.

2) ρ_Tj (x,y) – функция близости объектов по заданному опорному множеству.

3) Г = (γ _1, …,γ_m) – действительные числа (веса) – веса строк.

4) Вычисление оценок.

X ¹ P= { p ₁ ,…,p_n } – признаковое пр-во.

X ² – веса.

X ^ω

 

 

1. Система опорных множеств

T ¹, T ², …, Tⁿ, Tⁱ {1, …, n } – подмножество множества стобцов. В простейшем случае подмножество одно – это все матрица.

 

2. Функция близости по опорному множеству

 

. Построить ее можно, например, так:

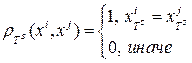
Но эту функцию можно строить и по другому: если больше 1 признака совпадает, или если больше 50% совпадает.

 

3. Вычисление функции близости по xⁱ

В самом простом случае Г (x^ω, xⁱ) = γ_i ρ (x^ω, xⁱ) – функция близости к искомому

объекту с учетом доверия ему к классу.

В общем случае формула примет вид: Г(x^ω, xⁱ) = F(γ_i ρ (x^ω, xⁱ))

 

4. Вычисление функции по классу

в – близость к каждому классу.

5. Решающее правило

Теперь задаем решающее правило – max, min и т.п., и определяем по нему принадлежность.

В общем случае этот алгоритм является параметрическим. A (Г, ρ, M), где Г, ρ, M – некий набор параметров, - изначально помимо обучающей выборки были известны прецеденты; параметры подгонялись так, чтобы известные прецеденты попадали по алгоритму в верные классы.

Сериальное кодирование

Здесь А = (0,1) и B = (0,1,…,9,*). Здесь символ * играет роль разделителя.

В данном примере битовые последовательности кодируются натуральными числами. Как это следует из свойств данного кодирование, оно дает эффект сжатия, когда битовые последовательности представляют собой чередование сравнительно больших блоков нулей и единиц.

Алгоритм кодирования. Пусть дана битовая последовательность α и а 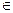(0,1) ее первый символ. Блоком назовем часть последовательности, состоящую из одинаковых символов. Тогда любую битовую последовательность можно представить как чередование блоков из нулей и единиц. Пусть в последовательности α всего S блоков, длина первого x₁, длина второго x₂,…, длина S –го - x_S. Тогда кодом α будет слово β=φ(α)=а* x₁* x₂*…* x_S.

Алгоритм декодирования очевиден.

Определение. Длиной сериального кода назовем число .

Определение. Средней длиной кода для n-последовательностей назовем число

,

Где сумма берется по всем двоичным последовательностям длины n.

Свойства кодирования определяются следующими двумя утверждениями.

Утверждение. .

Доказательство.

.

Утв. Средняя длина слова в сериальном кодировании
.

Из этих утверждений следует.

Таким образом, сериальное кодирование при малых количествах серий и большой длине серий приводит к тому, что при таком кодировании возникает эффект сжатия.

Если серии короткие и их много, например: и , то эффекта сжатия не возникает.

Алфавитное кодирование.

Если пренебречь разделителями, то в качестве двух алфавитов возьмем алфавиты

А = (а ₁, …, а_n) и B = (b ₁, …, b_q).

Алгоритм кодирования. Каждой букве a_i алфавита A ставится в соответствие B_i= φ(a_i) – слово в алфавите B длины l_i.

Алфавитное кодирование будет дешифруемым, если отображение индуцирует биекцию, т.е. для .

 

Обратим внимание на следующий важнейший факт, который, по сути дела, и оправдывает интерес к такому виду кодирования. Очевидно, что ограничение на вид отображения φ сразу влечет дешифруемость однобуквенных (в алфавите А) слов. Но из дешифруемости однобуквенных слов сразу следует дешифруемость слов (в алфавите A) любой длины.

Заметим также, что в случае дешифруемого кодирования все слова B_i= φ(a_i) обязательно различны.

Оказывается, что дешифруемость накладывает ограничение на набор длин кодовых слов. Об этом говорит утверждение, известное как неравенство Крафта.

Неравенство Крафта.

Теорема. Если алфавитное кодирование с длиной кодов l ₁, …, l_m дешифруемо, то выполняется неравенство:

Доказательство. Пусть А = (а ₁, …, а_n) и B = (b ₁, …, b_q). Каждой букве a_i алфавита A ставится в соответствие B_i= φ(a_i) – слово в алфавите B длины l_i. Положим

Пусть . Возведем Z в некоторую степень n, тогда

.

Здесь введено обозначение S (n, t) – число слов длины t и вида B_{i 1} B_{i 2} …B_in. Из дешифруемости следует, что все такие слова различны, но число различных слов длины t в алфавите из q букв не превосходит q^t, поэтому

S (n, t) q^t.

Тогда , где n – натуральное, а l ≥ 0, целое. Это неравенство должно выполняться для любого n, но это возможно только тогда, когда Z не превосходит единицы, т.е.

.

Утверждение доказано.

Префиксные коды.

Определение. Слово α является подсловом слова β, если существуют слова ϒ и ϑ (возможно пустые) такие, что β=ϒαϑ.

В общем случае из неравенства Крафта не следует дешифруемость.

Определение. Кодирование называется префиксным, если ни одно из кодовых слов не является началом другого.

Теорема. Префиксный код дешифруем.

Доказательство: Пусть есть α и β – два слова: φ (α) = Bi ₁ Bi ₂ …Bi_n, φ (β) = Bj ₁ Bj ₂ …Bj_n).

Покажем, что из равенства φ (α) = φ (β)следует равенство α = β.

Пусть Bi ₁ Bi ₂ …Bi_n = Bj ₁ Bj ₂ …Bj_n

Поочередно слева направо сравниваем подслова слов α и β, используя знание функции ϕ, которая определяет наше побуквенное кодирование (эта функция позволяет находить B_i= φ(a_i) среди подслов слов α и β. Сначала сравниваем Bi ₁= Bj ₁, затем переходим к Bi ₂и Bj ₂ и т.д.

Если длины слов Bi ₁и Bj ₁одинаковы, то сами слова должны быть одинаковыми из того, что Bi ₁ Bi ₂ …Bi_n = Bj ₁ Bj ₂ …Bj_n. Если длины слов разные, то одно из двух слов: Bi ₁или Bj ₁– начало другого, что противоречит определению префиксности.

Значит, α = β.

Теорема доказана.

Из теоремы сразу следует алгоритм декодирования префиксного кода.

Алгоритм декодирования. Берем первый символ слова φ (α)и ищем однобуквенное слово среди кодовых слов. Если находим такое слово, например, B_i= φ(a_i), то декодируем слово B_i= φ(a_i) в букву a_i и продолжаем работать, начиная со следующего символа слова φ (α). Если не находим, то добавляем следующий символ и ищем среди кодовых слов уже двухбуквенное слово. И т.д.

В случае алфавитного кодирования можно ограничиться префиксными кодами, так как, в каком-то смысле, любой дешифруемый алфавитный (побуквенный) код можно свести к префиксному. А существование префиксного кода полностью определяется неравенством Крафта.

Теорема (о существовании префиксного кода). Префиксный код с длинами кодов l ₁ … l_n существует тогда и только тогда, когда выполняется неравенство Крафта

.

Доказательство. Т.к. префиксный код дешифруем, то выполняется неравенство Крафта. С другой стороны, пусть выполняется неравенство Крафта. Покажем, что в этом случае существует префиксный код. Мы просто опишем алгоритм построения такого кода, т.е. построим отображение B_i= φ(a_i).

Пусть . Пусть среди чисел l ₁ … l_n имеется S ₁ единиц, S ₂ двоек, S ₃ троек и т.д. до S _l слов длины l. При этом некоторые из S _i могут быть нулями. Упорядочим B_i= φ(a_i) по возрастанию длины.

B ₁ = | l ₁| = 1

B ₂ = | l ₂| = 1 S ₁ слов длины 1

…

B_{S 1} = | l_{S 1}| = 1

B _{S 1+1} = | l _{S 1+1}| = 2

S ₂ слов длины 2

…

 

Тогда левую часть неравенства Крафта можно представить в виде:

S ₁ S ₂ S ₃

Теперь пошагово строим наш префиксный код.

Первый шаг: Любые S ₁ букв в B можно использовать для кодирования слов длины. Это следует из того, что при выполнении неравенства Крафта справедливо соотношение: S ₁/ q ≤ 1, из которого следует, что S ₁ ≤ q. Таким образом мы получили первую группу однобуквенных слов.

Второй шаг: Аналогично из неравенства Крафта получаем S ₁/ q + S ₂/ q ≤ 1. Отсюда S ₁ q + S ₂ ≤ q ², S ₂ ≤ q ² – s ₁ q. Поэтому можно взять S ₂ слов длины 2 в алфавите B так, что они не начинаются со слов первой группы. Таким образом мы получили вторую группу двухбуквенных слов.

Третий шаг: На этом шаге строим группу трехбуквенных слов так, чтобы они не начинались с ранее построенных слов. Такие трехбуквенные слова в нужном количестве существуют, так как вновь из неравенства Крафта следует, что S ₁ /q + S ₂ /q + S₃ / q ≤ 1. А это означает, что S₃ ≤ q³ – qS ₂ – q ² S ₁.

Таким образом проходим все l шагов и в результате получаем дешифруемый префиксный код.

Теорема доказана.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: