Математическая модель: алфавитное кодирование случайного источника.

Рассмотрим следующую модель. Имеется источник, который поочередно генерирует буквы алфавита A= (a ₁ …a_n) с вероятностями p ₁ …p_n. То есть имеет место следующая ситуация.

Каждая буква a_i генерируется с некоторой вероятностью p_i. Эта вероятность p_i не зависит от того, что выдал источник ранее и что он будет выдавать потом. Она также не зависит от очередности выдачи букв источником и от того, какой по счету от начала выдачи выдана данная буква. Такой источник называется источником Бернулли, что является частным случаем стационарного источника. На практике встречаются и другие источники. Для них приведенный ниже результаты неверны, но могут быть получены их аналоги.

Энтропия по Шеннону

Опр. Энтропией случайного источника (энтропией Шеннона) называется число

H (A) = .

В качестве замечания приведем следующее рассмотрение, которое показывает, почему данная формула выглядит именно так.

Пусть мы хотим ввести меру µ (A), которая характеризовала бы случайный источник.

Наложим на меру ограничения:

1) µ (A) = φ (p ₁ …p_n)

2) µ (A) ≥ 0, µ (A) < M

3) A×A – опыт на множестве A – 2 раза. Вероятность генерации следующей буквы не зависит от предыдущей итерации. φ (n ²) исходов. φ (n^k) = k φ (n)

4) φ (n) – монотонна по n

5) p ₁ < … p_n = 1 /n → φ (n) схожа с энтропией по Хартли.

Пусть a, n – целые неотрицательные числа.

Для любых a, n существует k: 2 ^k ≤ aⁿ ≤ 2 ^{k+ 1}

(1)

k < n log a < k+ 1

Применим монотонность φ к (1):

φ (2 ^k) ≤ φ (aⁿ) ≤ φ (2 ^{k+ 1})

k φ (2) ≤ n φ (a) ≤ (k+ 1) φ (2)

k k +1

 

(поделим на n и устремим к ∞)

φ (a) – φ (ε)log a → 0

φ (a) = φ (2)log a (возникает в 5 случае) – мера неопределенности

φ (n) = φ (2)log n – константа, необходимая для различия 2 элементов, полагаем ее равной 1 (отсюда и следует понятие бита)

Опыт A:

Пусть p_i – рациональные числа, p ₁ …p_k, n – НОК знаменателей p_i.

Тогда

Опыт B:

n равновероятных событий разобьем на k групп .

Сначала определим, в какой группе необходимо исследовать события. Тогда

Энтропия по Шеннону и энтропия по Хартли.

Заметим, что Энтропия по Хартли является частным случаем энтропии по Шеннону. Если все , то H (A) = log n, а это и есть Энтропия по Хартли множества из n элементов.В общем случае справедливо следующее утверждение, которое показывает, что энтропия по Хартли является оценкой сверху для энтропии по Шеннону. То есть ситуация равновероятных событий наихудшая с точки зрения информативности.

В следующем и других доказательствах нам потребуется математический факт, известный как неравенство Йенсена.

Неравенство Йенсена. Пусть даны числа α ₁ …α_n, α_i> 0, . Тогда для выпуклой вверх функции f(x) справедливо неравенство.

Теорема: Пусть имеется случайный источник, который генерирует буквы алфавита A = (a ₁ …a_n) с вероятностями p ₁ …p_n, тогда справедливо соотношение

H (A) = .

Доказательство. Рассмотрим функцию f (x) = -x log x. Так как f’ (x) = - log x – 1 /ln 2 и f’’ (x) = - 1 /x, то при

x ≥ 0 функция f (x) выпукла вверх. Тогда для нее справедливо неравенство Йенсена:

Возьмем α ₁ …α_n, α_i> 0,

 

 

Положим a_i = 1 /n, x_i = p_i,i=1,…,n.

H (A) =

Здесь мы учли, что .

Теорема доказана.

Теорема Шеннона

Рассмотрим теперь математическую модель, являющуюся объединением двух предыдущих. Случайный источник генерирует буквы алфавита А = (а ₁, …, а_n), к которым потом применяется некоторый алгоритм алфавитного кодирования φ. (Каждой букве a_i алфавита A ставится в соответствие B_i= φ(a_i) – слово длины l_i в алфавите B = (b ₁, …, b_q)). Как можно оценить качество такого алгоритма?

В случае вероятностного источника такие количественные характеристики алгоритма как или уже не являются информативными, так как не зависят от вероятностей.

В этом случае удобно использовать величину , которая характеризует среднее количество букв алфавита B, приходящееся на один символ алфавита A при алфавитном кодировании ϕ. (Назовем эту величину стоимостью кодирования ϕ). Пусть теперь , где минимум берется по всем возможным дешифруемым алгоритмам алфавитного кодирования (при заданных алфавитах A и B и распределении вероятностей p ₁ …p_n). (Назовем эту величину минимальной стоимостью кодирования).

Если бы мы знали C(A), то смогли бы оценить качество нашего алгоритма ϕ.

Следующая теорема (она известна под названием теоремы Шеннона для канала без шума) дает ответ на этот практически важный вопрос.

Теорема. Справедливо соотношение

.

Доказательство.

1) Сначала докажем оценку снизу

.

В следующих выкладках все суммы берутся по i=1,..,n. Используется известное из математического анализа неравенство l n x x – 1, log x log e (x – 1), а также неравенство Крафта.

( – по неравенству Крафта, ).

2) Для доказательства оценки сверху мы построим конкретный алгоритм алфавитного кодирования ϕ (известный как алгоритм Шеннона-Фано). Ведь если оценка сверху будет выполняться для некоторого C_ϕ(A), то она будет выполняться и для C(A).

В данном коде набор длин задается следующим соотношением.

(целая часть с избытком (сверху)).

Проверим, удовлетворяет ли этот набор неравенству Крафта.

, неравенство выполняется.

Теперь построим код точно также, как это делалось выше при доказательстве теоремы о существовании префиксного кода. Оценим теперь сверху величину C_ϕ(A) для этого кода.

C_ϕ(A) = .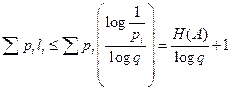

Теорема доказана.

Для случая бинарного алфавита В получаем неравенство

Н (А) С (А) Н (А) + 1.

Пример. Рассмотрим алфавит А = {0,…,9}. Ниже приведены два способа префиксного дешифруемого кодирования цифр бинарными последовательностями. Первый способ – это простой перевод в двоичную запись.

I способ 0 0000 II способ: 0 000

1 0001 1 010

2 0010 2 001

3 0011 3 011

4 0100 4 100

5 0101 5 101

6 0110 6 1100

7 0111 7 1101

8 1000 8 1110

9 1001 9 1111

На рисунке по колонками приведены значения C_ϕ(A) для обоих способов в предположении, что цифры генерируются случайным источником равновероятно. Из теоремы Шеннона следует оценка

С(А) Н(А) =

Второй алгоритм дает достаточно близкий результат. (На самом деле можно показать, что для данного случайного источника С(А)=3,4.)

Свойства энтропии.

Здесь в качестве справки мы приведем некоторые свойства энтропии по Шеннону. Это даст вам возможность лучше понять смысл этого понятия и сферу его практического применения.

Случайный источник можно трактовать как событие с множеством исходов, вероятности которых заданы.

Рассмотрим два события X и Y. Исходы первого события будем обозначать через x, а второго - через y. Введем по определению понятие условной энтропии H(X/y).

H (X|y) = .

Это случайная величина. А теперь усредним H (X|y) по всему множеству Y и получим уже неслучайную величину H (X|Y).

Перейдем теперь к перечислению свойств. В некоторых случаях приводятся доказательства.

1) H (X) 0.

2) H (X) является выпуклой вверх функцией своих аргументов функция своих аргументов p ₁ …p_n.

3) H (X) log|X| (если все события равновероятны, то энтропия максимальна).

4) H (X|Y) H (X) (Аналог свойства 3 для условной энтропии. Дополнительная

информация не увеличивает энтропию).

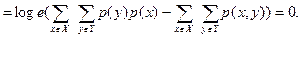
5) Пусть Х и Y – независимые события. Справедливо равенство

H (XY) = H (X) + H (Y).

6) Пусть два события имеют равное число исходов, а вероятности этих исходов как множества совпадают, т.е. они состоят из одних и тех же (p ₁,…, p_n), но в разном порядке. Справедливо равенство

H (X) = H (X ’).

7) Пусть есть событие Х = (p ₁,…, p_n) и некоторое подмножество его исходов А (p ₁,…, p_n). Построим новое событие Х_А таким образом, что его исходы задаются вероятностями («сглаживание» фрагмента).

Справедливо неравенство

H (х) H (Х_А).

Доказательство. Доказательство следует из свойств следует из (2) и (6).

По свойству (2) энтропия выпуклая вверх функция своих аргументов, а для такой функции f выполняется неравенство Йенсена .(Здесь числа α ₁ …α_n, α_i> 0, .)

Без ограничения общности считаем, что первые m элементов Х образуют подмножество А, т.е. исходы X задаются вероятностями p ₁ …p_mp_{m+ 1} …p_n

Строим вспомогательные события:

X ¹ = X

X ² = p ₂ p₃…p_mp ₁ p_{m+ 1} …p_n

X³ = p₃p₄…p ₁ p ₂ p_{m+ 1} …p_n

X^m = p_mp ₁ …p_{m- 2} p_{m- 1} p_{m+ 1} …p_n

Из свойства (6)следует, что H (X) = H (X¹) = … = H (X ^m) (все события состоит из одинаковых множеств значений вероятностей). Тогда можно Х_А представить в виде (H (X) + H (X¹)+ … + H (X ^m))/m. Применяем неравенство Йенсена, где все α_i=1/m. Получаем H(Х_А)≥ (H (X) + H (X¹)+ … + H (X ^m))/m. Отсюда следуетH(Х_А)≥H(A).

8) H (XY) = H (X) + H (Y|X) = H (Y) + H (X|Y).

Следует из известных в теории вероятностей соотношений: P (XY) = P (X) P (Y | X) и P (XY) = P (Y) P (X|Y).

9) H (X ₁ X ₂ …X_n) = H (X ₁) + H (X ₂ | X ₁) + H (X₃| X ₁ X ₂) + … + H (X_n| X ₁ X ₂ … X_{n- 1}).

Следует из известных в теории вероятностей соотношения: P (X ₁ …X_n) = P (X ₁) P (X ₂| X ₁) … P(X_n|X₁,…,X_n-1).

10) H (X|YZ) H (X|Y).

Доказывается по аналогии с доказательством свойства (4).

11) Пустьзадано событие X и на множестве его исходов определена функция y = g (x). Введем событие Y с множеством исходов y = g (x). Тогда H (Y) H (X). Равенство H (Y) = H (X) достигается тогда и только тогда, когда существует обратная функция g ^{– 1}.

Доказательство. Следует из свойства (8).

H (X) + H (Y|X) = H (Y) + H (X|Y) H (Y) = H (X) + H (Y|X) – H (X|Y) 0.

Т.к. у полностью определяется по х, то H (Y|X) = 0.

Алгоритмы кодирования

Алгоритм Шеннона (Фано)

Есть некоторые буквы:

 

(кодируем номером числа в двоичном виде)

H = 1/4 log 4 + 1/4 log 4 + 1/8 log 8 + 1/8 log 8 + 1/8 log 8 + 2 * 1/16 log 16 = 1 + 9/8 + 1/2 = 2, 625

Шаги алгоритма:

1) Упорядочиваем по вероятности

2) «Дихотомия»: разбиваем на части, вероятности которых одинаковы.

Таким образом:

a ₁ 00

a ₂ 01

a ₃ 100

a ₄ 101

a ₅ 110

a ₆ 1110

a ₇ 1111

l_ш = 21/7 = 3

Пример:

 

l = 3, l_ш = 12/5 = 2,4

H = 7/18 log 18/7 + 1/2 log 6 + 1/5 log 9 = 2,17

 

Алгоритм Хаффмана

Заведомо дает меньшее решение, чем по Шеннону.

a ₁ 1/4

a ₂ 1/4

a ₃ 1/8

a ₄ 1/8

a ₅ 1/8

a ₆ 1/16

a ₇ 1/16

В этом алгоритме идут итерации, по сути это построение листьев бинарного дерева. (1, 2, 3, 4, 5, 6, 7) → (1, 2, 3, 4, 5, (6, 7)) → (1, 2, (3, 4), 5, (6, 7)) → (1, 2, (3, 4), (5, 6, 7)) → ((1, 2), (3, 4), (5, 6, 7)) → ((1, 2), (3, 4, 5, 6, 7))

Теперь, начиная с конца, строим бинарное дерево:

 

и код:

1 00

2 01

3 100

4 101

5 110

6 1110

7 1111

Блочное кодирование

Поток из 0 и 1 будем интерпретировать как пары:

a 00 1/16 000

b 01 3/16 001

c 10 3/16 01

d 11 9/16 1

H (xx) = H (x) + H (x) = 2 H (x) = 1,62

Хаффман: (a, b, c, d) → ((a, b), c, d) → (a, b, c), d)

 

l (xx) = ∑ p_i l_i = 3/16 + 9/16 + 6/16 + 9/16 = 27/16

l (x) = 27/32 = 0, 844

a 000 1/64 00000

b 001 3/64 00001

c 010 3/64 00010

d 011 9/64 010

e 100 3/64 00011

f 101 9/64 001

g 110 9/64 001

h 111 27/64 1

(a, b, c, D, e, f, g, H) → ((a, b), c, D, e, f, g, H) → ((a, b), (c, e), D, f, g, H) → ((a, b, c, e), D, f, g, H) → ((a, b, c, e), (D, f), g, H) → ((a, b, c, e, g), (D, f), H) → ((a, b, c, D, e, f, g), H)

 

 

 

l = 5/64 + 15/64 + 15/64 + 15/64 +28/64 + 15/64 +27/64 +27/64 +27/64 = 50/64 +108/64 = 158/64 = 2,46875

Тогда:

X → l = 1

XX → l = 0,844

XXX → l = 0,823

H = 0,81

Пусть q (количество букв в кодируемом алфавите) = 2:

H (α) ≤ l (x) ≤ H (x) + 1

l (x) – 1 ≤ H (x) ≤ l (x)

H^k (x) = H (xx….x) → (по т. Шеннона) l^k (x) – 1 ≤ H^k (x) ≤ l^k (x)

Тогда H^k (x) = k H (x)

По определению l^k (x) = k l (x) (правильнее l (x) = 1 /k l^k (x)). Получим: l (x) – 1 /k ≤ H (x) ≤ l (x). Устремляем к бесконечности и делаем l (x) сколь угодно близким к H (x).

За такую точность приходится платить трудоемкостью алгоритмов кодирования (декодирования).

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: