 |
Схема и принципы кодирования.
|
|
|
|
Вероятность ошибки p (p < 1/2).
Теперь считаем, что источник выдает двоичное слово, и в двоичном симметричном канале шум представляет собой искажение символа с вероятностью 0< p <1/2.
|
|
|
Опр. Пропускная способность канала
C (p) = 1 – H (p)
- энтропия канала.
Пусть Bn - булев куб размерности n.
Опр. Кодом C называется произвольное подмножество 
.
Пусть M – мощность множества C.
Опр. Скорость передачи кода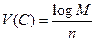 
.
Опр. Расстояние Хемминга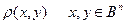 
.
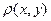= количество различных бит в x и y.
Пусть | x | - количество единиц в 
(норма x).
Опр. Кодовое расстояние 
.
Опр. (n,M,d)-код – это код C, такой, что | C | = M, C = { xi }, xi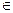 
Bn, d (C) = d.
Схемы кодирования могут быть самые разные. Рассмотрим одну из самых известных.
В ее основе лежит два принципа:
- Принцип наибольшего правдоподобия. Этот принцип вытекает из очевидного соотношения
pn < pn- 1(1 -p) < pn- 2(1 -p)2 < … < (1 -p) n (*)
и говорит о том, что вероятность k ошибок с кодовом слове меньше, чем вероятность s ошибок для всех s>k.
- Принцип избыточности.
Схема кодирования по наибольшему правдоподобию
|
|
|
|
Шар Bn, в нем 2 n точек.
M < 2 n
Стараемся, чтобы каждую из этих точек можно было окружить шаром радиуса t так, чтобы эти шары не пересекались.
pn < pn- 1(1 -p) < pn- 2(1 -p)2 < … < (1 -p) n (*)
(*) следует из того, что p < 1/2.
Это значит, что вероятность того, что ошибок не будет, больше, чем того, что будет одна ошибка и т.д. Это единственное обоснование схемы кодирования по наибольшему правдоподобию.
Дешифруем Yi. В xi на расстоянии 1 в шаре стоят все векторы, которые получились бы с одной ошибкой, на расстоянии 2 все векторы с двумя ошибками и т.д.
Возможны 3 случая:
|
|
|
1) Yi оказалась в шаре с центром в xi – произошло менее, чем d ошибок, 
;
2) Yi не попадает ни в один из шаров, 
для любого j;
3) 
(попала не в этот шар, а в соседний).
Если выполняется первый случай, то Yi → xi. Если третий, то Yi → xj, декодирование неверное.
Во втором случае обычно декодируют Yi в xj, тоже ошибка декодирования.
Пример:
C: a = 11 → x 1 = 11 000
b = 00 → x 2 = 00 110
c = 10 → x 3 = 10 011
d = 01 → x 4 = 01 101
11001 
| 00111
| 10010
| 01100
|
| 11010
| 00100
| 10001
| 01111
|
| 11100
| 00010
| 10111
| 01001
|
| 10000
| 01110
| 11011
| 00101
|
| 01000
| 10110
| 00011
| 11101
|
Источник Кодер B 5
a x 1
b x 1 → канал 
c x 1 C – (5,4,3)-код
d x 1
|
|
|
Если d = 2 t + 1, то шары вокруг кодовых слов строим радиуса t.
Если d = 2 t + 2, то шары радиуса t.
Тогда здесь каждое кодовое слово окружаем шаром радиуса 1.
Если получили любое слово из первых пяти строк таблицы, то декодирование произойдет правильно. Если же взять другое слово, то декодирование произойдет либо правильно, либо нет.
Т.о. куда отнести не вошедшее слово – часть не алгоритма декодирования, а схемы декодирования.
Код не обязан быть систематическим.
Корректирующие способности кодов. Границы мощности.
Пусть k – число информационных символов. Закодировали 2 k слов.
C (p) = 1 – H (p) – доля канала, предназначенного для информации.
Ниже (теорема Шеннона для канала с шумом) будет показано, что существуют коды, когда для любого Ԑ V(C) и 1- H(p) отличаются на Ԑ.
Опр. Код называется кодом, исправляющим t ошибок, если алгоритм декодирования
правильно декодирует все слова, в которых при передаче по каналу произошло
не более t ошибок.
Утверждение. (n,M,d)-код – код с исправлением 
ошибок.
Есть еще коды, обнаруживающие ошибки.
Опр. Код называется кодом, обнаруживающим t ошибок, если в случае, когда
произошло не более t ошибок, декодер выдает сообщение об ошибке.
|
|
|
Утверждение. (n,M,d)-код обнаруживает 
ошибку.
Мажоритарное кодирование – схема, где слово повторяется p раз.
a = 11 → 11|10|11|00|11|11|11 – передали по каналу 7 раз.
На первой позиции 6 раз «1» и 1 раз «0» 
a = 1х.
На второй позиции 5 раз «1» и 2 раза «0» a = 11.
Избыточность огромна. Уместно при высоких p (~1/10), при p~1/1000 уже бессмысленно.
Введем A (n,d) – максимальная мощность кода в Bn с расстоянием d.
Утверждение. Пусть есть множество V= (α1… αk),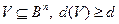 
. Также есть множество V’= (β1… βS), 
и для любых x, y 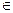V’: 
множества 
не пересекаются.
Доказательство. От противного.
где 
, 
.
|
|
|
