Комбинаторное доказательство теоремы.

Теорема Шеннона:

P *(M,n,p) 1, R < 1 – H(p).

Доказательство:

Пусть (есть , код , где V_k – коды C.

Тогда P *(V_k) – вероятность правильного декодирования для V_k.

Рассмотрим 3 функции:

Тогда P *(V_k) = - вероятность правильного декодирования.

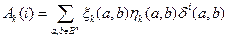- если выполняются все три условия , расстояние от a до b равно i, b декодируется в a, вероятность правильного декодирования – это число точек в , которые находятся на расстоянии i от некоторого кодового слова и декодируются в это кодовое слово.

//Всего таких кодов : .

P *(M,n,p) =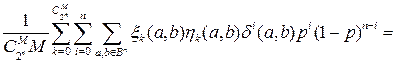

Остальную (M -1) точку выбирают произвольно:

a – ближайшая из всех кодовых точек.

, где - количество точек из в шаре радиуса .

Так сколько же кодов, где ?

 

Есть несколько моментов:

1) Функция C_x выпукла вверх.

2) Сумма выпуклых функций выпукла.

3) Выпуклая функция от выпуклой функции выпукла.

- выпукла тоже вверх.

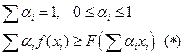
- выпукла вниз.

В качестве α_i возьмем , где

α_i =

Используя и получим .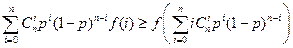

P *(M,n,p) = ,

 

где

 

Линейные коды

Опр.: Код C 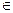Bⁿ называется групповым, если для любых α, β 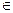C: α + β 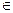C; групповому

коду обязательно принадлежит нулевой вектор.

Если код не является бинарным, то понятия линейного и групповых кодов не совпадают. В случае бинарного кода: Bⁿ – линейное пространство; зададим в нем подмножество векторов C 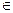Bⁿ, и для любых α, β 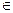C: α + β 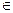C → подмножеству принадлежит линейная комбинация → C – подпространство Bⁿ. Пусть dimC = k, | C | = 2 ^k. Согласно определению: если C – групповой код, d (c) = min | α | (α 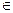С, α 0).

Для любого линейного кода существуют 2 матрицы: G – порождающая, H – проверочная.

Для любого β *принадлежит* C: β – линейная комбинация строк G. Если dimC = k, то G должна содержать k строк.

При построении кода (алгоритмов кодирования и декодирования) C не используется, чаще используется матрица H.

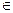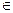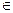Опр.: Код С* Bⁿ называется ортогональным C, если для любых α, β: α С*, β С,

αβ = 0. Если dimC = k, то dimC* = n – k. При этом порождающей матрицей С*

является проверочная матрица кода С H.

Свойства H: для любого α 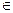С, αH^T = 0.

Пример: Код с проверкой на четность.

dimC = n – 1, dimH = 1, H = (11…1)_{1x n}

Вся алгоритмика – решение систем уравнений на линейных полях.

Элементарные преобразования матриц:

1) Перемена местами строк.

2) Умножение строки на число.

3) Сложение строки с линейной комбинацией других строк.

4) Перемена столбцов местами.

Опр.: Коды C и D называются эквивалентными, если G (C) можно получить из G (D) с

помощью элементарных преобразований.

Утверждение: Для любого С существует эквивалентный код С’ такой, что

В находятся информационные столбцы, в 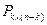- проверочные столбцы.

Опр.: Код с порождающей матрицей вида () называется систематическим.

 

 

В систематическом коде именно первые k символов являются информационными, без P G (C’) является просто порождающей матрицей всего кода. Проверочных символов (n – k). В H (C’) (n – k) строк, каждая строка – соотношение, задающее линейную комбинацию: 1-я – 10…0, 2-я – 01…0 и т.д.

Пример:

n = 5, k = 3 и

//Пусть α ₁, α ₂, α ₃ – информационные символы, α ₄, α ₅ – проверочные.

Алгоритм кодирования осуществляется следующим образом: любая строка H дает проверочную комбинацию.

d (C) = 2

Утверждение: d (C) = d, любые (d – 1) столбцов H линейно-независимые.

Для линейных кодов используется алгоритм декодирования «стандартная расстановка».

Опр.: Синдром линейного кода S = αH^T.

Если v 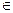C → S = 0.

Пусть вектор 11110, S = (1 0) ^T.

Для кодирования используется матрица стандартной расстановки. 1-я строка – код, 2-я строка – некодовые вектора с минимальным количеством единиц, складываем ее со всеми кодовыми векторами.

00000 10011 01010 11001 00101 10110 01111 11100

00001 10010 01011 11000 00100 10111 01110 11101

00010 10001 01000 11011 00111 10100 01101 11110

10000 00011 11010 01001 10101 00110 11111 01100

Разбиваем Bⁿ с помощью С на смежные классы, образующие этих классов – 1-й столбец. Когда декодируем, вектор, попавший в 1 столбец, декодируем в верхнее кодовое слово.

Утверждение: U – кодовое слово, U→ U+ e, e – вектор ошибки; стандартная расстановка правильно декодирует тогда и только тогда, когда вектор ошибки – образующая смежного класса. Целью построения является нахождение таких кодов, которые при минимальном числе строк содержали бы максимальное число линейно-независимых столбцом.

Приведем теперь два примера известных кодов.

Пример. Код Хемминга.

Пусть m – натуральное число. Проверочная матрица кода имеет размеры m x (2^m-1).

В столбцах находятся все ненулевые последовательности длины m, представляющие собой двоичную запись числа – номера столбца. Очевидно, что любые два столбца линейно независимы, а среди троек столбцов уже есть линейно зависимые наборы. Поэтому согласно приведенной выше теореме кодовое расстояние кода Хемминга d = 3. Следовательно этот код исправляет ровно одну ошибку.

Длина кодовых слов n = 2 ^m – 1. Число проверочных символов m = log (n + 1). Число информационных символов равно 2 ^m – 1 - m. Отсюда следует, что число кодовых слов | C | в коде Хэмминга | C | = 2 ⁿ / (1 + n).

Заметим теперь, что число точек в шаре радиуса единица равно 1 + n, и вспомним приведенную выше границу Хэмминга:

Код Хемминга исправляет одну ошибку и A (n, 3) = 2 / (1 + n). Получаем, что для Хемминга граница Хемминга достигается, «шары вокруг кодовых точек покрывают все пространство Bⁿ».

Опр.: Код С, исправляющий t ошибок, называется совершенным, если . Совершенный код – код, на котором достигается граница Хемминга.

Сразу из определения проверочной матрицы кода Хэмминга следует простой алгоритм декодирования. Декодирование происходит сразу после вычисления синдрома принятого слова y. Для принятого слова y есть три возможности:

1. Ошибок не было. Тогда синдром S = y H^T=0.
2. Ошибка ровно одна. Тогда синдром является двоичной записью (индикатором) номера бита, в котором произошла ошибка.
3. Произошло более одной ошибки. Тогда код Хэмминга не обеспечивает защиты от ошибок.

Пример:

m = 3, n = 2³ – 1 = 7, k = 4. Пусть информационными будут символы ().

U = 1100 → 0 1 1 1 1 0 0

 

Если U – передано, U ’ – получено, рассмотрим 3 случая:

С Заметим, что в данном примере

В общем случае мы получаем, что синдром это UH^T = - сумма «локаторов ошибок».

Задача: Построить код, исправляющий t ошибок.

⇐ Предыдущая123456789

Поделиться:

Воспользуйтесь поиском по сайту: