 |
Кодирование информации. Количество информации. Сжатие информации.
|
|
|
|
Итак, условие задачи – это информация, текст алгоритма – информация, результат работы алгоритма – информация и т.п. Еще раз хочу подчеркнуть, что нет алгоритма без информации и наоборот.
Сначала поясним, что будет пониматься под количеством информации, кодированием информации и сжатием информации.
Будем считать, что информация создается и используется человеком (субъектом).
Как мы уже говорили, при математическом подходе к информации предполагается справедливость следующего тезиса.
Тезис. Любая информация может быть представлена словом в конечном алфавите.
Очевидно, что множество слов может быть представлено одним словом. (Например, с помощью операции конкатенации.)
Опр. Конкатенация слов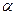 
и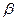 
получается путем последовательной записи символов одного слова вслед за символами другого, т.е.
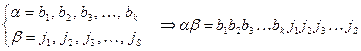
Поэтому понятия кодирование информации, количества информации и сжатие информации могут относиться как к одному слову, так и к множеству слов.
Кодирование информации – это создание слова α в алфавите А.
Количество информации – это некоторая количественная характеристика H(α), сопоставляемая слову (множеству слов) α.
Сжатие информации - это преобразование одного слова α в другое слово β. Поэтому сжатие – это преобразование информации, которое можно задать с помощью некоторого отображения φ. Таким образом, β=φ(α).
Вообще говоря, термин сжатие информации тесно связан с понятием количества информации. Сжатие происходит тогда, когда количество информации, приходящейся на один символ исходного слова α меньше, чем количество информации, приходящейся на один символ слова β=φ (α).
Кодирование информации.
|
|
|
Понятие кодирование применительно к информации будет рассматриваться в двух аспектах:
1. Создание самого Информационного объекта. То есть нанесение на материальный носитель информации о некотором объекте в виде слова α в алфавите А. В этом случае данное слово будет рассматриваться как код объекта. То есть код объекта – это символ интерпретации субъектом информации об объекте. (Назовем это кодированием в широком аспекте.)
2. Преобразование информации. Вначале информация была представлена словом α, а затем эта же информация представляется словом β, которое получено из α в результате некоторого преобразования φ. Тогда слово β=φ(α) называется кодом слова α. (Назовем это просто кодированием.)
 | |||
 | |||
Первый аспект возникает тогда, например, в программировании, когда нужно представить объект в виде набора данных. Эта проблема возникает как для математических объектов: числа, фигуры, группы, поля, алгоритмы и т.п., так и для объектов из других областей знаний: месторождения в геологии, болезни в медицине, каталоги в промышленности и т.п. Здесь результатом кодирования является слово, в то время как исходный объект кодирования либо представляет собой формализованный математический объект, либо вообще не формализован.
В Теории информации, как математической дисциплине, под кодированием понимался чаще всего второй случай. Здесь исходный и конечный объект кодирования – слова в алфавите.
Часто бывает, что кодирование (создание Информационного объекта) - это итерационный процесс. То есть, сначала есть объект B, есть информация о нём I(B), потом есть информация об информации о нём I(I(B)) и т.д. В результате можно получить некоторую структуру данных, состоящую из всех таких информаций.
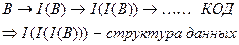
Количество символов в слове α будем называть длиной слова α и обозначать через l(α).
|
|
|
Примеры кодировок
Приведем простые примеры кодирования объектов.
1) Целые числа
Целое число n может быть представлено (закодировано), например, следующими тремя способами.
а) Словом α = 01…10 (n штук «1» и 0 по бокам) в алфавите А=(0,1). В этом случае длина кода l(α) (количество символов алфавита в слове) равна n+2;
б) Словом α = a 1 a 2 …ak в виде десятичной записи алфавите А=(0,1,…,9). Длина кода равна lg n.
в) В мультипликативной форме (произведение степеней простых множителей) в виде слова α = a 1 p 1 a 2 p 2 …akpk, (здесь a 1 … ak – простые числа).
Длина кода: 
.
2) Вектора и матрицы
Вектор с компонентами a 1 … an, записанными в десятичной форме имеет, может быть представлен в виде слова длины lg n + 
.
Матрица M с компонентами в десятичной форме, M=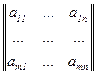 
, может быть представлена словом длины lg n + lg m + 
.
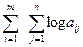3) G = ( V, E ) – неориентированный граф.
Здесь множество вершин обозначено через V, а множество ребер через E. Пусть |V| = n, |E| = m.
Граф можно представить, например, следующими тремя способами (все числа в десятичной форме)
а) Списком ребер {(i 1, j 1), (i 2, j 2), …, (im, jm)}.
б) Списком соседей (вершин), записанных последовательно для вершины 1, вершины 2,…, вершины n.
в) Матрицей смежности
A = | aij |m×n, 
.
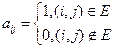Алфавит А кроме арабских цифр будет включать вспомогательные разделители, например, «,» и «;».
Длина кода l(α) без учета разделителей для каждого из трех случаев следующая:
а) 4n + 1 0m ≤ l(α) ≤4n + 1 0m + (n+ 2 n).
б) 2 n + 8m ≤ l(α) ≤ 2 n + 8m + 2log n.
в) l(α) = n 2 – n – 1.
Пример.
 |
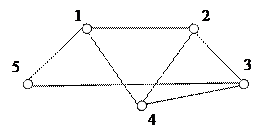1) (1 2), (1 5), (2 3), (3 4), (2 4), (5 3)
2) (2 4 5), (3 4), (4 5)
3) 
Свойства кодировок
К коду объекта α обычно применяют следующие требования.
Декодируемость. В случае кодирования (как преобразования слов) это свойство не вызывает вопросов. Пусть есть объект α, код β= φ(α). Декодируемость означает умение восстанавливать α по коду β= φ(α). В случае же кодирования в широком аспекте словом является только β. Сам объект α словом не является. Поэтому в каждом конкретном случае нужно определять понятие восстановление. В качестве примера можно привести пример присвоения идентификатора (слово в алфавите) неформализованному объекту (изделие, книга, человек). Здесь под восстановлением понимается нахождение конкретного объекта по его идентификатору.
|
|
|
Неизбыточность. Это требование означает стремление уменьшить длину кода. Но пока речь не идет об оптимизации и минимизации. Неизбыточность в широком смысле означает не поиск минимально возможной (по длине кода) кодировки, а использование известной кодировки без искусственного увеличения ее длины.
Разумность. Это термин из теории сложности алгоритмов. Он означает, что способ кодировки должен соответствовать тем целям, для которых информация будет использоваться в дальнейшем. Например, если мы решаем задачу о простоте числа (по заданному натуральному числу N требуется ответить на вопрос, является ли это число простым), то кодировка в мультипликативной форме (см. пример выше) не является разумной. Для большинства практических задач кодировка а) числа n в Примере 1 не является разумной.
Пусть мы теперь имеем "разумные" кодировки. На этом уровне принимается интуитивная гипотеза о некоторой эквивалентности всех возможных "разумных" кодировок входных данных одной и той же массовой задачи.
Второй пример показывает варианты длины кодировок в зависимости от способа задания чисел. Варианты длины кодировок в третьем примере зависят уже от структуры входных данных. Но в обоих случаях можно говорить о, так называемой, полиномиальной эквивалентности.
В дальнейшем нам полезно будет понятие полиномиальной эквивалентности двух функций. Две неотрицательные функции S(n) и R(n) полиномиально эквивалентны, если существуют два полинома Q(x) и P(x) такие, что для всех n справедливы неравенства S(n)£P(R(n)) и R(n)£Q(S(n)).
Пусть S и R две "разумные" схемы кодирования задачи массовой Z. Длины входа в этих схемах для задачи I обозначим через S(I) и R(I). К ним можно применить определение полиномиальной эквивалентности.
В третьем примере все три схемы полиномиально эквивалентны, а во втором полиномиально эквивалентны две последние.
|
|
|
