Интегрирование рациональных дробей

Вопрос.

Приемы нахождения неопределенных интегралов. Интегрирование рациональных дробей

Пусть подынтегральное выражение есть рациональная дробь где и - полиномы (многочлены) степеней k и n соответственно. Не умаляя общности, можем считать, что k < n, так как в противном случае всегда можно представить числитель в виде P(x) = Q(x)R(x) + S(x) где R(x)и S(x) -полиномы, называемые обычно, как и в случае действительных чисел, частным и остатком, причем степень полинома S(x) меньше n. Тогда

, (1.1)

а интеграл от полинома R(x) мы вычислять умеем. Покажем на примере, как можно получить разложение (1.1). Пусть
P(x) = x⁷ + 3x⁶ + 3x⁵ – 3x₃ + 4x₂ + x -2, Q(x) = x + 3x² + x-2. Разделим полином P(x) на полином Q(x) так же, как мы делим вещественные числа (решение получаем через калькулятор деления столбиком). Имеем

Таким образом, мы получили целую часть дроби (частное от деления полинома P на полином Q) R(x) = x⁴ + 2x² – 4x + 7 и остаток S(x) = 9x² – 14x +12 от этого деления.
По основной теореме алгебры [6] любой полином может быть разложен на простейшие множители, то есть представлен в виде , где – корни полинома Q(x) повторенные столько раз, какова их кратность.
Пусть полином Q(x) имеет n различных корней . Тогда правильная рациональная дробь может быть представлена в ви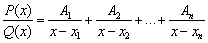де , где - числа подлежащие определению. Если - корень кратности α, то ему в разложении на простейшие дроби соответствует α слагаемых 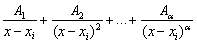. Если x_j- комплексный корень кратности полинома с действительными коэффициентами, то комплексно сопряженное число - тоже корень кратности α этого полинома. 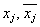Чтобы не иметь дело с комплексными числами при интегрировании рациональных дробей, слагаемые в разложении правильной рациональной дроби, соответствующие парам комплексно сопряженных корней, объединяют и записывают одним слагаемым вида , если – корни кратности один. Если 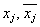– корни кратности , то им соответствует слагаемых и соответствующее разложение имеет вид

.

Таким образом, интегрирование правильных рациональных дробей свелось к интегрированию простейших дробей, из которых являются табличными, 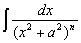может быть найден по рекуррентной формуле 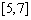, которая получается интегрированием по частям. Интегралы , 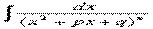в случае, когда знаменатель имеет комплексные корни (дискриминант ), сводятся, с помощью выделения полного квадрата, к интегралам , 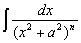заменой .
Одним из способов нахождения коэффициентов в разложении правильной рациональной дроби является следующий. Правую часть полученного разложения с неопределенными коэффициентами приводят к общему знаменателю. Так как знаменатели правой и левой частей равны, то должны быть равны и числители, которые являются полиномами. Приравнивая коэффициенты при одинаковых степенях (так как полиномы равны, если равны коэффициенты при одинаковых степенях ), получаем систему линейных уравнений для определения этих коэффициентов.

ПРИМЕРЫ
1. Найти .
Корни знаменателя – x₁ = -2 кратности 1 и x₂=1 кратности 2. Поэтому x³ – 3x + 2 = (x+2)(x-1)² и подынтегральная функция может быть представлена в виде

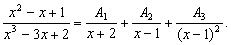
Приводя к общему знаменателю, получаем

Приравнивая коэффициенты при одинаковых степенях x в числителях правой и левой частей последнего соотношения, получаем

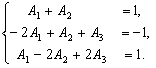
Решая эту систему, находим .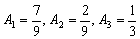
Таким образом,

ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ И ИРРАЦИОНАЛЬНОСТЕЙ

Интегрирование рациональных дробей

Интегрирование некоторых видов иррациональностей

Интегрирование рациональных дробей

Рациональной дробью называется дробь P (x)/ Q (x), числитель P (x) и знаменатель Q (x) которой – многочлены. Рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе.

У любой неправильной дроби можно выделить её целую часть. Для этого следует по правилу деления многочленов разделить числитель на знаменатель. Поэтому любую неправильную дробь можно представить в виде суммы её целой части и некоторой правильной дроби.

Например, неправильную дробь

Таким образом, если необходимо проинтегрировать неправильную дробь, то, представив её в виде суммы многочлена и правильной дроби, с помощью метода разложения сведём решение к интегрированию правильной дроби.

Ограничимся интегрированием лишь правильных рациональных дробей, знаменателями которых являются многочлены первой и второй степени. В общем виде интегралы от таких дробей записываются следующим образом:

(18)

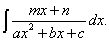(19)

При интегрировании дробей можно использовать следующую формулу, получаемую с помощью метода замены переменной:

(20)

Пример 1. Найти

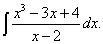
Подынтегральная функция является неправильной рациональной дробью. Используя приведённое выше её представление в виде суммы многочлена и правильной дроби, а также формулу (20), последовательно получим

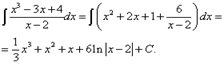
Любой интеграл вида (19) сводится к нахождению одного или двух следующих интегралов:

(21)

Поэтому рассмотрим эти интегралы. Первый из них находится по формуле (20) при a = 1.
Чтобы найти второй интеграл, воспользуемся тождеством

(22)

На основании тождества (22) получим

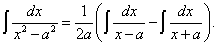
Используя формулу (20), имеем

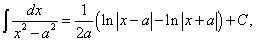
откуда после потенцирования в правой части равенства получаем

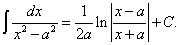(23)

Найдём теперь

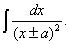
Здесь знаменатель подынтегрального выражения есть функция от , а числитель – её дифференциал. Поэтому произведя замену переменной

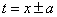
(тогда dt = dx) и применяя формулу (6) при n = - 2, получим

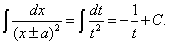
Вернувшись к старой переменной, окончательно имеем

(24)

Далее, найдём

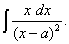
Так как

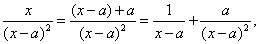
то

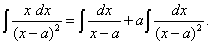
Применяя формулы (20) и (24), получим

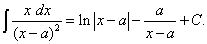
Интеграл

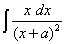
находится так же, как и предыдущий. В результате получим

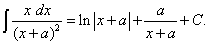
Последние две формулы можно записать в виде одной:

(25)

Найдём теперь

Заметив, что числитель подынтегрального выражения с точностью до постоянного множителя совпадает с дифференциалом знаменателя, полагаем

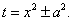
Тогда dt = 2 x dx, а x dx = (1/2) dt, откуда

Возвращаясь к старой переменной, окончательно получим

(26)

Найдём, наконец,

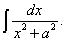
С помощью замены переменной x = at (тогда dx = a dt) данный интеграл приводится к табличному интегралу (14):

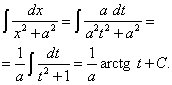
Возвращаясь к старой переменной, получим формулу

(27)

которая является обобщением табличного интеграла (14).

Формулы (23)-(27) можно условно считать табличными интегралами. С их помощью можно найти любой интеграл вида (19). Предварительно такой интеграл приводят к интегралам группы (21). Для этого в знаменателе подынтегральной функции выделяют полный квадрат и представляют его в одном из следующих видов:

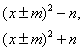
или

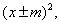
где m > 0 и n > 0.

В первых двух случаях замена переменной

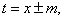
в третьем непосредственное применение метода разложения приведёт к одному или двум интегралам группы (21).

 

74 вопрос

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: