 |
Полная и приведенная системы вычетов
|
|
|
|
Определение. Числа 
образуют полную систему вычетов по модулю 
, если любое целое число сравнимо по модулю с одним и только одним из этих чисел.
Любая полная система вычетов по модулю состоит из чисел, которые попарно не сравнимы по модулю .
Теорема. Пусть 
— полная система вычетов по модулю . Пусть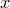 
— целое число, взаимно простое с . Тогда 
— тоже полная система вычетов по модулю .
Доказательство. Нужно доказать, что эти числа попарно не сравнимы по модулю . Предположим противное. Пусть
Так как НОД 
, то 
, что противоречит условию.
Теорема. Пусть — полная система вычетов по модулю . Пусть 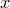— целое число. Тогда 
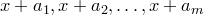— тоже полная система вычетов по модулю .
Лемма. Если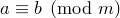 
, то НОД 
НОД 
.
Доказательство.
– целое число.
Отсюда 
. Любой общий делитель 
и является делителем 
. Отсюда НОД НОД .
Определение. Числа образуют приведенную систему вычетов по модулю , если они взаимно просты с и любое целое число, взаимно простое с , сравнимо с одним и только одним из этих чисел по модулю .
Пример. Приведенная система вычетов по модулю 10: 1,3,7,9.
Лемма. Все приведенные системы вычетов по модулю состоят из одного и того же количества чисел, которое обозначается 
— функция Эйлера.
Доказательство. Действительно, пусть есть две приведенные системы вычетов по модулю , состоящие из разного количества чисел:
Тогда так как числа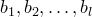 
образуют приведенную систему вычетов по модулю , то каждое из чисел 
сравнимо с одним и только одним из этих чисел. Поскольку 
, то, по принципу Дирихле, по крайней мере два числа из будут сравнимы с каким-то числом 
, а значит, будут сравнимы между собой по модулю . А это противоречит тому, что — приведенная система вычетов по модулю . Значит,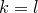 
.
|
|
|
Докажем теперь, что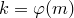 
. В самом деле, числа, меньшие и взаимно простые с , образуют приведенную систему вычетов по модулю . Это следует из леммы.
Определение. Функция Эйлера (или тотиент) обозначает количество чисел, меньших и взаимно простых с .
Теорема. Если — приведенная система вычетов по модулю и 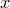— число, взаимно простое с , то 
— тоже приведенная система вычетов по модулю .
Если 
— простое, то 
.
Лемма. Если — простое, то 
.
Доказательство. Действительно, чисел, меньших простого и имеющих с ним общий делитель, всего 
.
Лемма. Пусть НОД 
. Тогда 
. Функция Эйлера мультипликативна.
Доказательство. Запишем все числа от 1 до 
следующим образом:
Числа в каждой строке образуют полную систему вычетов по модулю . Значит, взаимно простых с среди них 
. При этом эти числа расположены по столбцам — друг под другом, поскольку в каждом столбце стоят числа, сравнимые по модулю .
Числа в каждом столбце образуют полную систему вычетов по модулю . Действительно, 
-й столбец получается, если взять числа 
, образующие полную систему вычетов по модулю , умножить их на число , взаимно простое с , и прибавить к каждому из них .
Таким образом, в каждом столбце ровно 
чисел, взаимно простых с .
Так как число будет взаимно простым с тогда и только тогда, когда оно взаимно просто с и взаимно просто с , то количество чисел, взаимно простых с , равно 
.
Теорема. Пусть
— каноническое разложение числа . Тогда
Доказательство. По лемме о мультипликативности функции Эйлера
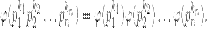
А далее каждое 
вычисляем по лемме о вычислении функции Эйлера для простых чисел.
Пример.
Теорема (Эйлера). Есл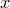и и — взаимно простые числа, то
Пусть — какая-нибудь приведенная система вычетов по модулю . . 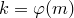Тогда — тоже приведенная система вычетов по модулю . Следовательно, каждое из чисел первой последовательности сравнимо с одним из чисел второй последовательности по модулю , а каждое из чисел второй последовательности сравнимо с одним из чисел первой последовательности. Тогда
|
|
|
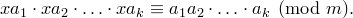
Так как каждое из чисел взаимно просто с , то на них сравнение можно сократить:
Следствие. Пусть 
– целые числа, 
– натуральные. Если ,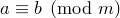 
, НОД 
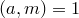, то 
.
Доказательство. Пусть 
. Так как , то 
– натуральное число. Тогда
.
Значит, .
88вопрос
Гомотетия и подобие пространства
- Гомотетией пространства с центром O и коэффициентом k ≠ 0 называется преобразование пространства, при котором любая точка М отображается на такую точку М', что
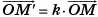
Гомотетию с центром O и коэффициентом k обозначают Hk0
- Подобием пространства с коэффициентом k (k >0) называется такое преобразование пространства, при котором расстояние между любыми двумя точками изменяется в k раз, то есть для любых двух точек А и В длина отрезка А'B' равна k
| AB |, где А ' = Рk (A) и B '= Рk (В).Подобие пространства называют также преобразованием подобия. Если при этом подобии фигура F отображается на фигуру F ', то пишут Рk (F)= F' и говорят, что фигура F' подобна фигуре F.
Свойства преобразований гомотетии и подобия пространства аналогичны свойствам гомотетии и подобия плоскости, поэтому изучение первых следует начинать с повторения вторых. Подобие пространства с коэффициентом k можно разложить в композицию движения и гомотетии с некоторым центром и тем же коэффициентом.
Учащиеся должны знать, что при подобном преобразовании пространства сохраняется величина угла (плоского и двугранного), параллельные (перпендикулярные) прямые и плоскости отображаются на параллельные (перпендикулярные) прямые и плоскости. Это означает, что при подобном преобразовании пространства образом любой фигуры является фигура, имеющая такую же форму, что и данная фигура, но отличающаяся от нее лишь «своими размерами».
Задача 12. Дан правильный тетраэдр РАВС; точки Р 1, А 1, В 1, С 1 — центры его граней (рис.14). Докажите, что тетраэдр Р 1 А 1 В 1 С 1подобен тетраэдру РАВС; найдите коэффициент этого подобия.
Рис. 14
Решение. Пусть точки Н и K — середины ребер соответственно АВ и ВС тетраэдра РАВС, точка А 1 — центр грани РВС, точка Р 1 — центр грани АВС (рис. 14). Это означает, что
РА 1: А 1 K = АР 1: Р 1 K = 2: 1,
откуда
А 1 K: РK = Р 1 K: АK = 1: 3,
|
|
|
Аналогично можно доказать, что
А1В1: АВ = 1: 3 и А1В1 
АВ,
А1С1: АС = 1: 3 и А1С1 АС,
В1С1: ВС = 1: 3 и В1С1 ВС,
В1Р1: ВР = 1: 3 и В1Р1 ВР,
С1Р1: СР = 1: 3 и С1Р1 СР.
Из этих соотношений между ребрами тетраэдров РАВС и Р1А1В1С1 следует, что тетраэдр Р1А1В1С1 — правильный, поэтому эти тетраэдры подобны; коэффициент подобия равен 1/3. (В профильных классах стоит доказать, что эти тетраэдры гомотетичны.)
Можно ввести определение: «Фигура F1 называется подобной фигуре F, если существует преобразование подобия пространства, отображающее фигуру F на фигуру F1». Тогда для доказательства подобия фигуры F1 фигуре F достаточно найти хотя бы одно преобразование подобия, которое фигуру F отображает на фигуру F1..
90 вопрос
Определение. Параллельным переносом, или, короче, переносом фигуры, называется такое ее отображение, при котором все ее точки смещаются в одном и том же направлении на равные расстояния, т.е. при переносе каждым двум точкам X и Y фигуры сопоставляются такие точки X' и Y', что XX' = YY'
Основное свойство переноса:
Параллельный перенос сохраняет расстояния и направления, т.е. X'Y' = XY
Отсюда выходит, что параллельный перенос есть движение, сохраняющее направление и наоборот, движение, сохраняющее направление, есть параллельный перенос
Из этих утверждений также вытекает, что композиция параллельных переносов есть параллельный перенос
Параллельный перенос фигуры задается указанием одной пары соответствующих точек. Например, если указано, в какую точку A' переходит данная точка A, то этот перенос задан вектором AA', и это означает, что все точки смещаются на один и тот же вектор, т.е. XX' = AA' для всех точек Х
Центральная симметрия
Определение
Точки A и A' называются симметричными относительно точки О, если точки A, A', O лежат на одной прямой и OX = OX'. Точка О считается симметричной сама себе (относительно О)
Две фигуры называются симметричными относительно точки О, если для каждой точки одной фигуры есть симметричная ей относительно точки О точка в другой фигуре и обратно
Как частный случай, фигура может быть симметрична сама себе относительно некоей точки О. Тогда эта точка О называется центром симметрии фигуры, а фигура центрально-симметричной
|
|
|
Определение
Центральной симметрией фигуры относительно О называется такое отображение этой фигуры, которое сопоставляет каждой ее точке точку, симметричную относительно О
Основное свойство: Центральная симметрия сохраняет расстояние, а направление изменяет на противоположное. Иначе говоря, любым двум точкам X и Y фигуры F соответствуют такие точки X' и Y', что X'Y' = -XY
Доказательство. Пусть при центральной симметрии с центром в точке О точки X и Y отобразились на X' и Y'. Тогда, как ясно из определения центральной симметрии, OX' = -OX, OY' = -OY
Вместе с тем XY = OY - OX, X'Y' = OY' - OX'
Поэтому имеем: X'Y' = -OY + OX = -XY
Отсюда выходит, что центральная симметрия является движением, изменяющим направление на противоположное и наоборот, движение, изменяющее направление на противоположное, есть центральная симметрия
Центральная симметрия фигуры задается указанием одной пары существующих точек: если точка А отображается на А', то центр симметрии это середина отрезка AA'
Поворот вокруг прямой
Для более четкого представления о повороте вокруг прямой следует вспомнить поворот на плоскости около данной точки. Поворотом на плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из данной точки, поворачивается на один и тот же угол в одном и том же направлении. Перейдем теперь к повороту в пространстве
Определение. Поворотом фигуры вокруг прямой a на угол (называется такое отображение, при котором в каждой плоскости, перпендикулярной прямой a, происходит поворот вокруг точки ее пересечения с прямой a на один и тот же угол (в одном и том же направлении. Прямая a называется осью поворота, а угол - углом поворота)
Отсюда видим, что поворот всегда задается осью, углом и направлением поворота
Теорема 1. Поворот вокруг прямой сохраняет расстояния, т.е. является движением
Теорема 2. Если движение пространства имеет множеством своих неподвижных точек прямую, то оно является поворотом вокруг этой прямой
Преобразования плоскости
|
|
|
