 |
Определенный интеграл Римана
|
|
|
|
Напомним, что множество  точек отрезка [ a, b ] таких, что
точек отрезка [ a, b ] таких, что
a = x 0 < x 1 <... <  <
<  = b,
= b,
называется разбиением отрезка [ a, b ], a  R, b
R, b  R.
R.
Точки xk называются точками разбиения  , отрезки [ xk -1, xk ] - отрезками разбиения
, отрезки [ xk -1, xk ] - отрезками разбиения  ; их длины обозначаются
; их длины обозначаются  xk, т. е.
xk, т. е.  xk = xk - xk -1, k = 1, 2,...,
xk = xk - xk -1, k = 1, 2,...,  , а число
, а число
|  |
|  max{
max{  x 1,
x 1,  x 2,...
x 2,... 
 }
}
называемся мелкостью разбиения  .
.
Разбиение  называется разбиением, вписанным в разбиение
называется разбиением, вписанным в разбиение  , если
, если 

 *, т. е. если каждая точка разбиения
*, т. е. если каждая точка разбиения  содержится в разбиении
содержится в разбиении  *. В этом случае каждый отрезок [
*. В этом случае каждый отрезок [ 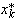 ,
,  ] разбиения содержится в некотором отрезке [ xj -1, xj ] разбиения
] разбиения содержится в некотором отрезке [ xj -1, xj ] разбиения  , j = 1, 2,...,
, j = 1, 2,...,  .
.
Разбиение  *, вписанное в разбиение
*, вписанное в разбиение  , называется также разбиением, следующим за разбиением
, называется также разбиением, следующим за разбиением  , и пишут
, и пишут  *
* 
 . В этом случае говорят также, что разбиение
. В этом случае говорят также, что разбиение  предшествует разбиению
предшествует разбиению  *, и пишут
*, и пишут 
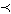
 *.
*.
Существенными являются следующие два свойства разбиений отрезка.
1o. Если 
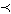
 ', а
', а  '
' 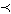
 ", то
", то 
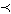
 ".
".
 Действительно, если каждый отрезок разбиения
Действительно, если каждый отрезок разбиения  " содержится в некотором отрезке разбиения
" содержится в некотором отрезке разбиения  ', а каждый отрезок разбиения
', а каждый отрезок разбиения  ' содержится в некотором отрезке разбиения
' содержится в некотором отрезке разбиения  , то каждый отрезок разбиения
, то каждый отрезок разбиения  " содержится в соответствующем отрезке разбиения
" содержится в соответствующем отрезке разбиения  .
. 
2o. Для любых разбиений  ' и
' и  " существует такое разбиение
" существует такое разбиение  , что
, что 

 ' и
' и 

 ".
".
 В самом деле, таким разбиением является, например, разбиение, состоящее из всех точек обоих разбиений
В самом деле, таким разбиением является, например, разбиение, состоящее из всех точек обоих разбиений  ' и
' и  ".
". 
Пусть функция f определена на отрезке [ a, b ], a < b, и  - некоторое разбиение этого отрезка. Всякая сумма
- некоторое разбиение этого отрезка. Всякая сумма  вида
вида

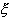 k
k  [ xk -1, xk ], k = 1, 2,...,
[ xk -1, xk ], k = 1, 2,...,  ,
,
называется интегральной суммой Римана функции f.
 Рис. 102 Рис. 102
|
В случае если функция f неотрицательна, то интегральная сумма  равна площади фигуры, составленной из прямоугольников с основанием [ xk -1, xk ] и высотой длины f (
равна площади фигуры, составленной из прямоугольников с основанием [ xk -1, xk ] и высотой длины f (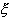 k) (рис. 102).
k) (рис. 102).
Определение 1. Функция f называется интегрируемой по Риману на отрезке [ a, b ], если для любой последовательности разбиений
|
|
|
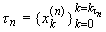 , n = 1, 2,...,
, n = 1, 2,...,
отрезка [ a, b ], мелкость которых стремится к нулю:  |
|  n | = 0, и для любого выбора точек
n | = 0, и для любого выбора точек  , k = 1, 2,...,
, k = 1, 2,...,  , последовательности интегральных сумм
, последовательности интегральных сумм
 , n = 1, 2,...,
, n = 1, 2,...,
имеют и притом один и тот же предел.
Этот предел называется интегралом Римана функции f по отрезку [ a, b ]. Его обозначают  и пишут
и пишут
 = =  . .
| (23.1) |
Согласно определению это означает, что если

 ,
,  ,
,
k = 1, 2,...,  ,
,
то

 =
=  ,
,
если только  |
|  n | = 0.
n | = 0.
Можно сформулировать определение интеграла Римана, и не используя понятия предела последовательности, а, как говорят, на "языке  -
-  ".
".
Определение 2. Число I называется интегралом Римана от функции f на отрезке [ a, b ], если для любого  > 0 существует такое
> 0 существует такое  > 0, что, каково бы ни было разбиение
> 0, что, каково бы ни было разбиение  отрезка [ a, b ], мелкость которого меньше
отрезка [ a, b ], мелкость которого меньше  : |
: |  | <
| <  , и каковы бы ни были точки
, и каковы бы ни были точки 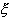 k
k  [ xk -1, xk ], k = 1, 2,...,
[ xk -1, xk ], k = 1, 2,...,  , выполняется неравенство
, выполняется неравенство
|  - I | <
- I | <  .
.
Аналогично равносильности определений предела функции в терминах последовательностей и в терминах окрестностей доказывается и равносильность определений 1 и 2 интеграла Римана. Это рекомендуется читателю проделать самостоятельно.
В интеграле  число a называется нижним, а число b - верхним пределом интегрирования. В дальнейшем для краткости вместо "функция, интегрируемая по Риману", будем говорить "интегрируемая функция", а вместо "интеграл Римана" - просто "интеграл". Дополним определение интеграла следующими соглашениями. Если функция f задана в точке x = a, то по определению
число a называется нижним, а число b - верхним пределом интегрирования. В дальнейшем для краткости вместо "функция, интегрируемая по Риману", будем говорить "интегрируемая функция", а вместо "интеграл Римана" - просто "интеграл". Дополним определение интеграла следующими соглашениями. Если функция f задана в точке x = a, то по определению  = 0. Если функция f интегрируема на отрезке [ a, b ], то положим
= 0. Если функция f интегрируема на отрезке [ a, b ], то положим


 .
.
Формула Ньютона-Лейбница
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
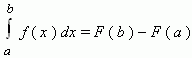
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x), вычислить ее значения в точках a и b и найти разность F(b) – F(a).
|
|
|
Если после изучения данного теоретического материала (Формула Ньютона-Лейбница) у Вас возникли проблемы при решении задач на данную тему или появились вопросы образовательного характера, то Вы всегда можете задать их на нашем форуме.
80 вопрос
|
|
|


