 |
Действительные числа в виде выражений
|
|
|
|
Из определения действительных чисел понятно, что действительными числами являются:
· любое натуральное число;
· любое целое число;
· любая обыкновенная дробь (как положительная, так и отрицательная);
· любое смешанное число;
· любая десятичная дробь (положительная, отрицательная, конечная, бесконечная периодическая, бесконечная непериодическая).
Но очень часто действительные числа можно видеть в виде корней, степеней, логарифмов и т.п. Более того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа (смотрите действия с действительными числами). К примеру,  - это действительные числа.
- это действительные числа.
А если пойти дальше, то из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций и т.п. можно составлять всевозможные числовые выражения, значения которых также будут действительными числами. Например, значения выражений 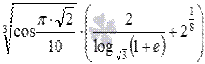 и
и  есть действительные числа.
есть действительные числа.
В заключение этой статьи заметим, что следующим этапом расширения понятия числа является переход от действительных чисел к комплексным числам.
Дедекиндово сечение (узкая щель) — один из способов построения вещественных чисел из рациональных. ВведёнДедекиндом.
Множество вещественных чисел определяется как множество дедекиндовых сечений. На них возможно продолжить операции сложения и умножения.
Определение
Дедекиндово сечение — это разбиение множества рациональных чисел  на два подмножества
на два подмножества  и
и 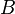 такие, что:
такие, что:
1. 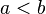 для любых
для любых  и
и 
2.  не имеет максимального элемента.
не имеет максимального элемента.
Пример
Дедекиндово сечение √2
Вещественному числу 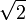 соответствует дедекиндово сечение, определяемое
соответствует дедекиндово сечение, определяемое
|
|
|
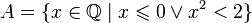 и
и
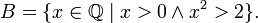
Интуитивно можно представить себе, что для того, чтобы определить 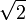 , мы рассекли множество на две части: все числа, что левее
, мы рассекли множество на две части: все числа, что левее 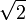 , и все числа, что правее
, и все числа, что правее 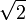 ; соответственно,
; соответственно, 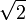 равен точной нижней грани множества
равен точной нижней грани множества 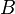 .
.
86 вопрос
Числовая последовательности и ее предел.
Функция f(x) называется функцией целочисленного аргумента, если множество значений x, для которых она определена, является множеством всех натуральных чисел1, 2, 3,… Примером функции целочисленного аргумента может служить сумма n первых чисел натурального ряда. В данном случае

Числовой последовательностью называется бесконечное множество чисел
 (1)
(1)
следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого 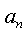 задается как функция целочисленного аргумента,
задается как функция целочисленного аргумента, 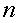 т.е.
т.е. 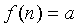 .
.
Число А называется пределом последовательности (1), если для любого 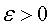 существует число
существует число 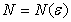 , такое, что при
, такое, что при 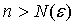 выполняется неравенство
выполняется неравенство 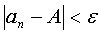 . Если число А есть предел последовательности (1), то пишут
. Если число А есть предел последовательности (1), то пишут
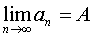
Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.
Для сходящихся последовательностей имеют место теоремы:
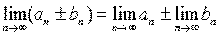
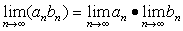
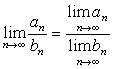
если 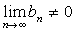 .
.
Пример 1.
Найти общий член последовательности 1, 4, 9, 16, 25, …
Р е ш е н и е: нетрудно видеть, что
 и т.д.
и т.д.
Следовательно 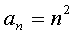
Пример 2.
Найти общий член последовательности 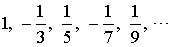
Р е ш е н и е: не трудно видеть, что
 ,
, 
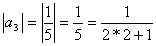 ,
, 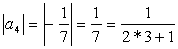 и т.д.
и т.д.
Следовательно:
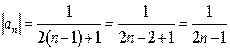
Числовая последовательность
Функция an=f (n) натурального аргумента n (n=1; 2; 3; 4;...) называется числовой последовательностью.
Числа a1; a2; a3; a4;…, образующие последовательность, называются членами числовой последовательности. Так a1=f (1); a2=f (2); a3=f (3); a4=f (4);…
Итак, члены последовательности обозначаются буквами с указанием индексов — порядковых номеров их членов: a1; a2; a3; a4;…, следовательно, a1 — первый член последовательности;
|
|
|
a2 - второй член последовательности;
a3 - третий член последовательности;
a4 - четвертый член последовательности и т.д.
Кратко числовую последовательность записывают так: an=f (n) или {an}.
Существуют следующие способы задания числовой последовательности:
1) Словесный способ. Представляет собой закономерность или правило расположения членов последовательности, описанный словами.
Пример 1. Написать последовательность всех неотрицательных чисел, кратных числу 5.
Решение. Так как на 5 делятся все числа, оканчивающиеся на 0 или на 5, то последовательность запишется так:
0; 5; 10; 15; 20; 25;...
Пример 2. Дана последовательность: 1; 4; 9; 16; 25; 36;.... Задайте ее словесным способом.
Решение. Замечаем, что 1=12; 4=22; 9=32; 16=42; 25=52; 36=62; … Делаем вывод: дана последовательность, состоящая из квадратов чисел натурального ряда.
2) Аналитический способ. Последовательность задается формулой n-го члена: an=f (n). По этой формуле можно найти любой член последовательности.
Пример 3. Известно выражение k-го члена числовой последовательности: ak = 3+2·(k+1). Вычислите первые четыре члена этой последовательности.
Решение.
a1=3+2∙(1+1)=3+4=7;
a2=3+2∙(2+1)=3+6=9;
a3=3+2∙(3+1)=3+8=11;
a4=3+2∙(4+1)=3+10=13.
Пример 4. Определите правило составления числовой последовательности по нескольким ее первым членам и выразите более простой формулой общий член последовательности: 1; 3; 5; 7; 9;....
Решение. Замечаем, что дана последовательность нечетных чисел. Любое нечетное число можно записать в виде: 2k-1, где k — натуральное число, т.е. k=1; 2; 3; 4;.... Ответ: ak=2k-1.
3) Рекуррентный способ. Последовательность также задается формулой, но не формулой общего члена, зависящей только от номера члена. Задается формула, по которой каждый следующий член находят через предыдущие члены. В случае рекуррентного способа задания функции всегда дополнительно задается один или несколько первых членов последовательности.
Пример 5. Выписать первые четыре члена последовательности {an},
если a1=7; an+1 = 5+an.
Решение.
a2 =5+a1=5+7=12;
a3 =5+a2=5+12=17;
a4 =5+a3=5+17=22. Ответ: 7; 12; 17; 22;....
Пример 6. Выписать первые пять членов последовательности {bn},
если b1 = -2, b2 = 3; bn+2 = 2bn +bn+1.
Решение.
b3 = 2∙b1 + b2 = 2∙(-2) + 3 = -4+3=-1;
b4 = 2∙b2 + b3 = 2∙3 +(-1) = 6 -1 = 5;
b5 = 2∙b3 + b4 = 2∙(-1) + 5 = -2 +5 = 3. Ответ: -2; 3; -1; 5; 3;....
|
|
|
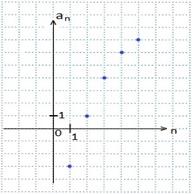
4) Графический способ. Числовая последовательность задается графиком, который представляет собой изолированные точки. Абсциссы этих точек — натуральные числа: n=1; 2; 3; 4;.... Ординаты — значения членов последовательности: a1; a2; a3; a4;….
Пример 7. Запишите все пять членов числовой последовательности, заданной графическим способом.
 Решение.
Решение.
Каждая точки в этой координатной плоскости имеет координаты (n; an). Выпишем координаты отмеченных точек по возрастанию абсциссы n.
Получаем: (1; -3), (2; 1), (3; 4), (4; 6), (5; 7).
Следовательно, a1= -3; a2=1; a3=4; a4=6; a5 =7.
Ответ: -3; 1; 4; 6; 7.
Рассмотренная числовая последовательность в качестве функции (в примере 7) задана на множестве первых пяти натуральных чисел (n=1; 2; 3; 4; 5), поэтому, является конечной числовой последовательностью (состоит из пяти членов).
Если числовая последовательность в качестве функции будет задана на всем множестве натуральных чисел, то такая последовательность будет бесконечной числовой последовательностью.
Числовую последовательность называют возрастающей, если ее члены возрастают (an+1>an) и убывающей, если ее члены убывают (an+1<an).
Возрастающая или убывающая числовые последовательности называются монотонными.
Из определения сходимости последовательности  к точке a вытекает, что для любого
к точке a вытекает, что для любого  интервалом длиной 2
интервалом длиной 2  можно накрыть всю эту последовательность, исключением может быть конечное число ее элементов, если середину интервала поместить в точке
можно накрыть всю эту последовательность, исключением может быть конечное число ее элементов, если середину интервала поместить в точке 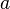 . Справедливо и обратное: если последовательность
. Справедливо и обратное: если последовательность  такова, что для любого
такова, что для любого  можно накрыть всю эту последовательность, исключая может быть конечное число ее элементов, поместив центр интервала в некоторую точку, то она сходится. Сформулируем это утверждение более точно.
можно накрыть всю эту последовательность, исключая может быть конечное число ее элементов, поместив центр интервала в некоторую точку, то она сходится. Сформулируем это утверждение более точно.
Определение. Подпоследовательность 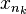 называется последовательностью Коши или фундаментальной, если
называется последовательностью Коши или фундаментальной, если
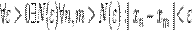
Теорема (Критерий Коши). Для того, чтобы последовательность  сходилась, необходимо и достаточно чтобы она была фундаментальной.
сходилась, необходимо и достаточно чтобы она была фундаментальной.
Доказательство:
Необходимость. Пусть  сходится.
сходится. 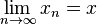
|
|
|
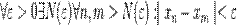
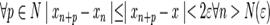
Достаточность. Пусть  - фундаментальная последовательность. Докажем, что она ограничена и
- фундаментальная последовательность. Докажем, что она ограничена и 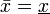 .
.
Так как последовательность фундаментальна, то 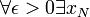 , в
, в  -окрестности которой существуют все элементы после
-окрестности которой существуют все элементы после 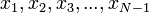 .
.
Предположим,  .
.
В отрезке [A, -A] содержатся все элементы последовательности, т.е.  - ограничена.
- ограничена.
Вследствие теоремы Больцано-Вейерштрасса ( ) < (
) < ( ).
).
 в силу произвольности
в силу произвольности 
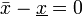
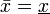
Из определения сходимости последовательности { xn } к точке a вытекает, что для любого 
 0 интервалом длиной 2
0 интервалом длиной 2  можно накрыть всю эту последовательность, исключая может быть конечное число ее элементов, если середину интервала поместить в точке a. Справедливо и обратное: если последовательность { xn } такова, что для любого
можно накрыть всю эту последовательность, исключая может быть конечное число ее элементов, если середину интервала поместить в точке a. Справедливо и обратное: если последовательность { xn } такова, что для любого 
 0 можно накрыть всю эту последовательность, исключая может быть конечное число ее элементов, поместив центр интервала в некоторую точку, то она сходится. Сформулируем это утверждение более точно. Последовательность { xn } назовем последовательностью Коши или фундаментальной, если
0 можно накрыть всю эту последовательность, исключая может быть конечное число ее элементов, поместив центр интервала в некоторую точку, то она сходится. Сформулируем это утверждение более точно. Последовательность { xn } назовем последовательностью Коши или фундаментальной, если
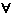   0 0 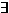 N ( N ( ) ) 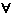 n, m n, m  N ( N ( ): | xn - xm | ): | xn - xm |  
| (4.4.1) |
(здесь центр интервала длиной 2  помещен в точку xm, m
помещен в точку xm, m  N (
N ( ), см. рис 4.4.1)
), см. рис 4.4.1)
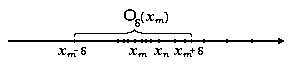
Рис. 4.4.1
Теорема 4.4.1 (Критерий Коши) Для того, чтобы последовательность { xn } сходилась, необходимо и достаточно чтобы она была фундаментальной.
Доказательство.Необходимость. Пусть xn 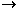 a при n
a при n 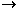
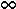 . Тогда для любого
. Тогда для любого 
 0 существует N (
0 существует N ( ), что для любых n, m
), что для любых n, m  N (
N ( ) выполняется | xn - a |
) выполняется | xn - a | 
 / 2, | xm - a |
/ 2, | xm - a | 
 / 2. Рассмотрим цепочку неравенств
/ 2. Рассмотрим цепочку неравенств
| xn - xm | = | (xn - a) + (a - xm) |  | xn - a | + | xm - a |
| xn - a | + | xm - a | 

что означает, что { xn } фундаментальна.
Достаточность. Докажем сначала ограниченность последовательности { xn }. Возьмем  = 1
= 1  0, тогда по фундаментальности { xn }, найдется N (
0, тогда по фундаментальности { xn }, найдется N ( ), что для всех n, m
), что для всех n, m  N (
N ( ) выполняется | xn - xm |
) выполняется | xn - xm |  1. Следовательно, | xn | - | xm |
1. Следовательно, | xn | - | xm |  | xn - xm |
| xn - xm |  1, поэтому | xn |
1, поэтому | xn |  1 + | xm |. Итак, для всех n
1 + | xm |. Итак, для всех n  N (
N ( ) при фиксированном m
) при фиксированном m  N (
N ( ) выполняется | xn |
) выполняется | xn |  1 + | xm |, что означает ограниченность последовательности
1 + | xm |, что означает ограниченность последовательности
{ xn }, (см. замечание 3.2.1). По теореме 4.3.2 из последовательности { xn } можно выделить подпослеловательность, сходящуюся к некоторому числу a. Докажем, что и вся последовательность сходится к числу a.
Возьмем любое 
 0, тогда найдется номер N (из фундаментальности { xn }), что для всех n, m
0, тогда найдется номер N (из фундаментальности { xn }), что для всех n, m  N выполняется | xn - xm |
N выполняется | xn - xm | 
 / 2. В виду сходимости xnk
/ 2. В виду сходимости xnk 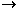 a при k
a при k 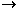
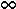 по взятому
по взятому 
 0 найдется номер k 0, такой, что nk 0
0 найдется номер k 0, такой, что nk 0  N и | xnk 0 - a |
N и | xnk 0 - a | 
 / 2. Тогда для любого n
/ 2. Тогда для любого n  N
N
| xn - a | = | xn - xm + xm - a | = [ xm = xnk 0 ]  | xn - xm | + | xnk 0 - a |
| xn - xm | + | xnk 0 - a | 
 ,
,
что означает сходимость последовательности { xn } к числу a.
св0во 1) Существование предела у монотонной и ограниченной последовательности (теорема 3.1.2).
2) Принцип вложенных отрезков (теорема 4.1.1).
3) Существование точной верхней границы у произвольного ограниченного сверху множества
(теорема 4.2.1).
4) Из ограниченной последовательности можно выделить сходящуюся подпоследовательность
(теорема 4.3.2)
5) Критерий Коши сходимости числовой последовательности (теорема 4.4.1)Хотя перечисленные свойства действительных чисел и выглядят различно, на самом деле у них имеется глубокая внутренняя связь. Можно показать, что все эти утверждения эквивалентны. Мы показали лишь, что из 1) следует 2), из 2) следует 3), из 2) следует 4), из 4) следует 5). Свойства 1) - 5) называются еще свойствами непрерывности или полноты множества действительных чисел 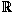 .
.
|
|
|
87 вопрос
|
|
|


