Вывод формул для площадей четырехугольников

Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле

где d ₁ и d ₂ – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).

Рис. 1

Доказательство. В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2. Площадь параллелограмма можно найти по формуле

S = a h_a,

где a – сторона параллелограмма, а h_a – высота, опущенная на эту сторону (рис. 2).

Рис. 2

Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

S_ABCD = S_AEFD = a h_a,

что и требовалось доказать.

Утверждение 3. Площадь параллелограмма можно найти по формуле

S = ab sin φ,

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

Рис. 3

Доказательство. Поскольку

h_a= b sin φ,

то, в силу утверждения 2, справедлива формула

S = a h_a= ab sin φ,

что и требовалось доказать.

76 вопрос

ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

43.1. Основные понятия

Пусть задано множество D упорядоченных пар чисел (х;у). Соответствие ƒ, которое каждой паре чисел (х; у) є D сопоставляет одно и только одно число z є R, называется функцией двух переменных, определенной на множестве D со значениями в Е, и записывается в виде z = ƒ(х;у) или ƒ: D→ R При этом х и у называются независимыми переменными (аргументами), а z — зависимой переменной (функцией).

Множество D = D(f) называется областью определения функции. Множество значений, принимаемых z в области определения, называется областью изменения этой функции, обозначается E(f) или Е.

Примером функции двух переменных может служить площадь S прямоугольника со сторонами, длины которых равны х и у: S = ху. Областью определения этой функции является множество {(х;у) | х > 0, у > 0}.

Функцию z = ƒ(х;у), где (х;у) є D можно понимать (рассматривать) как функцию точки М(х;у) координатной плоскости Оху. В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается D. Примером замкнутой области является круг с окружностью.

Значение функции z = ƒ(х;у) в точке М0(х0;у0) обозначают z0=ƒ(хо;уо) или z0=ƒ(М0) и называют частным значением функции.

Функция двух независимых переменных допускает геометрическое истолкование. Каждой точке М0(х₀; у₀) области D в системе координат Oxyz соответствует точка M(x₀;y₀;z₀), где z₀ = ƒ(х_о;у_о) — аппликата точки М. Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию z=ƒ(x;у).

Например, функция имеет областью определения круг х² + у² ≤ 1 и изображается верхней полусферой с центром в точке O(0;0;0) и радиусом R = 1 (см. рис. 205).

Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком. Будем пользоваться, как правило, аналитическим способом: когда функция задается с помощью формулы.

43.2. Предел функции

Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Множество всех точек М(х;у) плоскости, координаты которых удовлетворяют неравенству называется -окрестностью точки М₀(х₀;у₀). Другими словами, -окрестность точки М_о — это все внутренние точки круга с центром М_о и радиусом 8 (см. рис. 206).

Пусть функция z = ƒ(х; у) определена в некоторой окрестности точки М₀(х₀;у₀), кроме, быть может, самой этой точки. Число А называется пределом функции z = ƒ (х; у) при х → х₀ и у → у₀(или, что то же самое, при М(х; у) → М₀(х₀; у₀)), если для любого є > 0 существует  > 0 такое, что для всех х ≠ х₀ и у ≠ у₀и удовлетворяющих неравенству

выполняется неравенство | ƒ (х; у) — А| < є. Записывают:

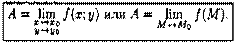
Из определения следует, что если предел существует, то он не зависит от пути, по которому М стремится к М_о (число таких направлений бесконечно; для функции одной переменной х→ х₀ по двум направлениям: справа и слева!)

Геометрический смысл предела функции двух переменных состоит в следующем. Каково бы ни было число є>0, найдется-окрестность точки M_о(х_о;у_о), что во всех ее точках М(х;у), отличных от М_о, аппликаты соответствующих точек поверхности z=ƒ(х;у) отличаются от числа А по модулю меньше, чем на є.

Пример 43.1. Найти предел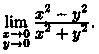

Решение: Будем приближаться к О(0;0) по прямой у=Кх, где К — некоторое число. Тогда

Функция в точке О(0; 0) предела не имеет, т. к. при разных значенияхК предел функции не одинаков (функция имеет различные предельные значения).

 

Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной (см. п. 17.3). Это означает, что справедливы утверждения: если функции ƒ (М) и g(М) определены на множестве D и имеют в точке М_о этого множества пределы А и В соответственно, то и функции ƒ(М) ± g(M), ƒ(М) • g(М), имеют в точке Мо пределы, которые соответственно равны А ± В, А • В, ^A/_B(В≠0).

 

43.3. Непрерывность функции двух переменных

Функция z = ƒ(х;у) (или ƒ(М)) называется непрерывной в точке М₀(х₀;у₀), если она:

а) определена в этой точке и некоторой ее окрестности,

б) имеет предел

в) этот предел равен значению функции z в точке М_о, т. е.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва z=ƒ(х;у) могут образовывать целые линии разрыва. Так, функция 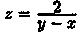имеет линию разрыва у=х.

Можно дать другое, равносильное приведенному выше, определение непрерывности функции z=ƒ(х;у) в точке. Обозначим Δх=х—х_0, Δу=у—у₀, Δz=ƒ(х;у)—ƒ(х₀;у₀). Величины Δх и Δу называются приращениями аргументов х и у, а Δz — полным приращением функции ƒ(х;у) в точке М₀(х₀;у₀).

Функция z = ƒ(х;у) называется непрерывной в точке М₀(х₀;у₀) є D, если выполняется равенство т. е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов х и у стремятся к нулю.

Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям — подобные теоремы имели место для функций одной переменной (см. п. 19.4).

 

Частные производные функции двух переменных.
Понятие и примеры решений

На данном уроке мы продолжим знакомство с функцией двух переменных и рассмотрим, пожалуй, самое распространенное тематическое задание – нахождение частных производных первого и второго порядка, а также полного дифференциала функции. Студенты-заочники, как правило, сталкиваются с частными производными на 1 курсе во 2 семестре. Причем, по моим наблюдениям, задание на нахождение частных производных практически всегда встречается на экзамене.

Для эффективного изучения нижеизложенного материала вам необходимо уметь более или менее уверенно находить «обычные» производные функции одной переменной. Научиться правильно обращаться с производными можно на уроках Как найти производную? и Производная сложной функции. Также нам потребуется таблица производных элементарных функций и правил дифференцирования, удобнее всего, если она будет под рукой в распечатанном виде. Раздобыть справочный материал можно на странице Математические формулы и таблицы.

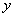Быстренько повторим понятие функции двух переменных, я постараюсь ограничиться самым минимумом. Функция двух переменных обычно записывается как , при этом переменные , называются независимыми переменными или аргументами.

Пример: – функция двух переменных.

Иногда используют запись . Также встречаются задания, где вместо буквы 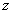используется буква .

С геометрической точки зрения функция двух переменных чаще всего представляет собой поверхность трехмерного пространства (плоскость, цилиндр, шар, параболоид, гиперболоид и т. д.). Но, собственно, это уже больше аналитическая геометрия, а у нас на повестке дня математический анализ, который никогда не давал списывать мой вузовский преподаватель является моим «коньком».

Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.

Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас:

Пример 1

Найти частные производные первого и второго порядка функции

Сначала найдем частные производные первого порядка. Их две.

Обозначения:
или – частная производная по «икс»
или – частная производная по «игрек»

Начнем с . Когда мы находим частную производную по «икс», то переменная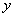 считается константой (постоянным числом).

Решаем:

Комментарии к выполненным действиям:

(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.

Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если вы где-нибудь нарисуете «штрих» без , то преподаватель, как минимум, может поставить рядом с заданием (сразу откусить часть балла за невнимательность).

Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.

(2) Используем правила дифференцирования , . Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как 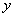считается константой, а любую константу можно вынести за знак производной, то мы выносим за скобки. То есть в данной ситуации ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое : здесь, наоборот, выносить нечего. Так как 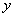константа, то – тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».

(3) Используем табличные производные и .

(4) Упрощаем, или, как я люблю говорить, «причесываем» ответ.

Теперь . Когда мы находим частную производную по «игрек», то переменная считается константой (постоянным числом).

(1) Используем те же правила дифференцирования , . В первом слагаемом выносим константу за знак производной, во втором слагаемом ничего вынести нельзя поскольку – уже константа.

(2) Используем таблицу производным элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива и для (да и вообще почти для любой буквы). В частности, используемые нами формулы выглядят так: и .

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: