 |
Формулы для вычисления площади треугольника
|
|
|
|
1. Из геометрии известна формула Г е р о н а:
S = \/р (р - а)(р - b) (р - с),
(где р = (а+ b+c)/2 -полупериметр), позволяющая вычислять площадь треугольника по его сторонам.
2. Теорема. Площадь треугольника равна половине произведения двух сторон на синус угла между ними:
S = 1/2 bc sin A.
Доказательство. Из геометрии известно, что площадь треугольника равна половине произведения стороны треугольника на высоту, опущенную на эту сторону из противоположной вершины.
S = 1/2 b · hb (1)
Если угол А острый, то из треугольника АВН найдём ВН = hb = с sin A.
Если угол A тупой, то ВН = hb = с sin ( -A) = с sin A. Если угол A прямой, то sin A = 1 и hb = АВ = с = с sin A.
Следовательно, во всех случаях hb = с sin A. Подставив в равенство (1), получим доказываемую формулу.
| 
|
Точно так же получим формулы: S = 1/2 ab sin C = 1/2 ac sin B
3. На основании теоремы синусов:
Подставив эти выражения в формулу (1), получим следующую формулу:
Пусть дан треугольник АВС, достроим его до параллелограмма АВСД, тругю АВС и ДСВ равны по трем сторонам (ВС-общая, АС=ВД как противоположные стороны параллелограмма,) их площади раывны. Следовательно площадь треуг АВС равна половине площади Параллелограммв АВСД, т.е. S1/2AB*CH
82 вопрос
Теорема Больцано-Вейерштрасса
Формулировка теоремы Больцано-Вейерштрасса
Теорема
Теорема Больцано-Вейерштрасса (или лемма Больцано-Вейерштрасса о предельной точке).
Из всякой ограниченной последовательности точек пространства 
можно выделить сходящуюся подпоследовательность.
Доказательство. Так как последовательность ограничена, то она имеет хотя бы одну предельную точку 
. В таком случае из этой последовательности можно выделить подпоследовательность, сходящуюся к точке .
|
|
|
Замечание 1
Из любой ограниченной последовательности можно выделитьмонотонную подпоследовательность.
Доказательство. Действительно, согласно теореме Больцано-Вейерштрасса, из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность, а из этой подпоследовательности можно выделить монотонную подпоследовательность.
Замечание 2
Пусть 
- ограниченная последовательность, элементы которой принадлежат промежутку 
. Тогда предел 
любой сходящейся подпоследовательности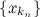 
этой последовательности также находится на сегменте .
Доказательство. Действительно, так как для любого номера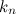 
имеет место соотношение 
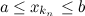, то в силу утверждения, что если все элементы сходящейся последовательности находятся на сегменте , то и ее предел также находится на этом сегменте, выполняются неравенства 
. То есть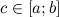 
.
Отметим, что в отдельных случаях и из неограниченной последовательности также можно выделить сходящуюся подпоследовательность. Например, последовательность 
- неограниченная, однако подпоследовательность 
ее элементов с четными номерами сходится.
Но не из каждой неограниченной последовательности можно выделить сходящуюся подпоследовательность. Например, любая подпоследовательность неограниченной последовательности 
расходится. Поэтому теорему Больцано-Вейерштрасса, вообще говоря, нельзя распространить на неограниченные последовательности.
Историческая справка
Теорема Больцано-Вейерштрасса (для случая 
) впервые была доказана чешским математиком, философом и теологом Бернардом Больцано (1781 - 1848) в 1817 году. В работе Больцано она выступала как лемма в доказательстве теоремы о промежуточных значениях непрерывной функции, известной теперь как теорема Больцано-Коши. Однако эти и другие результаты, доказанные Больцано задолго до Коши и Вейерштрасса, остались незамеченными. Лишь через полвека Вейерштрасс, независимо от Больцано, заново открыл и доказал эту теорему. Первоначально она называлась теоремой Вейерштрасса, до того как стали известны и получили признание работы Больцано.
|
|
|
Эта теорема используется при доказательстве многих предложений анализа, например, теоремы о достижении непрерывной на отрезке функцией своих точных верхней и нижней граней.
83 вопрос
3 Теоремы Эйлера и Ферма.
Теоремы Эйлера и Ферма являются основой всей теории сравнений и находят широкое применение как в теоретических исследованиях, так и в арифметических приложениях.
Теорема Эйлера. Если 
, то 
.
Доказательство. Рассмотрим ПрСВ наименьших неотрицательных по модулю 
(она едиственна): 
, 
(1). Так как , то числа 
(2) также образуют ПрСВ по модулю . Заменим числа системы (2) остатками от деления их на , получим ПрСВ наименьших неотрицательных по модулю , которая совпадет с системой (1), с точностью дол порядка следования чисел: 
, 
(3). Причем 
, перемножим эти сравнения, получим 
. Поскольку системы (1) и (3) равны, то сократив на них обе части полученного сравнения по свойствам сравнимости, получаем утверждение теоремы.
Теорема (малая) Ферма. Если 
- простое число, то 
.
Доказательство. 
. Если 
, то по теореме Эйлера следует, что 
, то есть 
. Если 
, то 
, то есть .
Пример 1. Найти остаток от деления числа 328 на 7.
Решение. Так как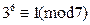 
, то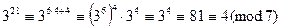 
.
Пример 2. Найти остаток от деления 243132 на 43.
Решение. Имеем 
. Так как 
, то согласно теореме Эйлера: 
или 
. Тогда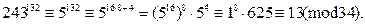 
Следовательно, искомый остаток равен 13.
Пример 3. Вычислить последние две цифры числа 
.
Решение. Последние две цифры числа образуют остаток при делении этого числа на 100, т.е. 
, где 
. Так как 
, то 
. 
поэтому теорему Эйлера Применить пока что нельзя. Положим 
, имеем 
, откуда 
. Применяем теорему Эйлера: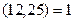 
, 
, 
, 
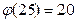. Тогда получаем 
. Так как 
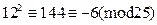, то 
, 
. Следовательно, 
, т.е. последние две цифры числа являются 9 и 6.
Теорема Ферма — Эйлера
[править | править вики-текст]
Материал из Википедии — свободной энциклопедии
Теорема Ферма-Эйлера или теорема о представлении простых чисел в виде суммы двух квадратов гласит[1]:
Нечётное простое число представимо в виде суммы двух квадратов (целых чисел) тогда и только тогда, когда оно имеет вид  . Иначе говоря: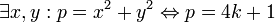 
|
В иностранной литературе это утверждение часто называют рождественской теоремой Ферма, так как она стала известна из письма Пьера Ферма, посланного 25 декабря 1640 года.
|
|
|
Примеры:
Из этого утверждения при помощи тождества Брахмагупты выводится общее утверждение:
Натуральное число представимо в виде суммы двух квадратов (целых чисел) тогда и только тогда, когда любое простое число вида  входит в его разложение на простые множители в чётной степени.
|
Иногда именно этот факт подразумевается под теоремой Ферма — Эйлера.
85 вопрс
|
|
|
