 |
Стандартизация и техническое регулирование
|
|
|
|
1. Представьте кратко этапы развития стандартизации.
2. Раскройте сущность стандартизации.
3. Назовите цели стандартизации.
4. Дайте классификацию объектов стандартизации.
5. Назовите сферу применения закона о техническом регулировании.
6. Назовите объекты технического регулирования.
7. Назовите основные принципы стандартизации.
8. Назовите основные принципы технического регулирования.
9. Назовите цели закона РФ «О техническом регулировании».
10.Раскройте сущность целей принятия технических регламентов.
11.Раскройте сущность комплексной стандартизации.
12.Раскройте сущность опережающей стандартизации.
13.Назовите документы в области стандартизации.
14.Назовите, какие существуют категории стандартов.
15.Расскажите о применении документов в области стандартизации.
16.Назовите виды национальных стандартов с краткой характеристикой.
17.Расскажите кратко о международной стандартизации (какие организации входят и их краткая характеристика).
18.Расскажите о порядке внедрения международных стандартов в России.
19.Расскажите о межгосударственной стандартизации (правила применения этих стандартов).
20.Расскажите о национальной стандартизации(кто разрабатывает программу и какова последовательность).
21.Назовите виды и характеристики технического регламентов.
22.Раскройте сущность роли стандартизации в системе технического регулирования.
23.Дайте характеристику структуры технических регламентов.
24.Расскажите о разработке технических регламентов.
25.Дайте краткую характеристику закона РФ «О техническом регулировании».
26.Расскажите о сфере применения технических регламентов.
27.Расскажите о порядке разработки и принятие технических регламентов.
|
|
|
28.Назовите причины отмены технических регламентов.
29.Расскажите о содержание технических регламентов.
30.Назовите виды и характеристики технических регламентов.
31.Раскройте основные функции ИСО.
32.Раскройте основные функции, цели и задачи МЭК.
33.Дайте характеристику основным функциям МСЭ.
34.Раскройте сущность локальной стандартизации (область применения, цели и функции).
35.Технические условия как нормативный документ.
36.Виды документов по стандартизации действующие на предприятии (краткая характеристика этих документов).
37.Расскажите об объектах стандартов организации.
38.Расскажите о разработке правил (рекомендации) в области стандартизации (кратко процесс разработки и рассмотрения первой редакции правил и окончательной).
39.Расскажите о порядке разработки стандартов организации.
40.Расскажите об общероссийском классификаторе продукции.
41.Расскажите в чем особенности стандартизации услуг.
42.Какими полномочиями обладают органы государственного контроля.
43.Расскажите об ответственности органов государственного контроля при осуществлении контроля за соблюдением требований технических регламентов.
44.Расскажите о предоставлении информации о несоответствии продукции требования технических регламентов.
45.Расскажите, в чем заключается обязанность изготовителя (продавца) в случае получения информации о несоответствии продукции требованиям технических регламентов.
46.Расскажите о правах органов государственного контроля в случае получения информации о несоответствии продукции требованиям технических регламентов.
47.Расскажите о принудительном отзыве продукции.
48.Расскажите кратко о федеральном информационном фонде технических регламентов и стандартов.
49.Расскажите, как происходит финансирование в области технического регулирования.
|
|
|
50.Расскажите кратко о значении стандартизации в современном мире.
51.Расскажите об органах и службы стандартизации РФ.
52.Расскажите, что входит в состав уровней системы документов технического регулирования.
53.Дайте характеристику требований к продукции.
54.Дайте общую характеристику и обоснование необходимости разработки стандартов организации.
55. Назовите особенности технического регулирования продукции.
56.Расскажите, в чем заключаются особенности технического регулирования в области обеспечения безопасности продукции, услуг.
57.Расскажите об органах государственного контроля(надзора) за соблюдением требований технических регламентов.
58.Расскажите что относится к объектам государственного контроля(надзора) за соблюдением требований технических регламентов.
59.Дайте краткую характеристику этапов реформирования системы стандартизации РФ.
60.Региональные организации по стандартизации и их деятельность.
ПРИМЕРЫ ВЫПОЛНЕНИЯ ПРАКТИЧЕСКИХ ЗАДАНИЙ
Примеры решения типовых задач
Пример 1.
При проведении измерительного эксперимента получены следующие значения величины: 11,65; 11,41; 11,57; 11,60; 11,50; 11,55; 11,58; 11,58; 11,61; 11,63. Требуется проанализировать полученные результаты наблюдений в целях выявления грубых погрешностей, используя критерий Диксона.
Решение:
1. Располагаем результаты наблюдений в вариационный возрастающий ряд:
11,41<11,50<11,55<11,57<11,58;11,58<11,60<11,61<11,63<11,65.
2. Записываем используемую для расчета формулу критерия Диксона:
 .
.
3. Подставляем в формулу данные нашего эксперимента и рассчитываем Кд:
 .
.
4. Зададимся значением q=0,10 (десятипроцентным уровнем значимости).
5. Используя табличные данные, выявим критическую область для рассчитанного критерия Кд.
Согласно табл. 2 приложения 3 при n=10 и q=0,15, zдикс =0,35.
6. Делаем вывод, что Кд < zдикс.
Ответ. Полученный ряд результатов наблюдений не имеет в своем составе грубых погрешностей даже при q=0,1. Дальнейшей обработке будет подвергаться весь массив данных.
Пример 2.
В процессе контроля были получены следующие результаты измерительных наблюдений за одним из показателей качества: 9,47; 9,49; 9,40; 9,61; 9,39; 9,41; 9,43; 9,49; 9,46; 9,42. Используя критерий Романовского выявить наличие промахов.
|
|
|
Решение:
1. Располагаем результаты в вариационный возрастающий ряд:
9,39<9,40<9,41<9,42<9,43<9,46<9,47<9,49<9,49<9,61.
2. Выявляем результат, вызывающий сомнение:
Результат 9,61 вызывает сомнение, так как резко отличается от всех остальных (хi=9,61).
3. Запишем основную расчетную формулу:  .
.
При расчете 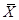 результат хi=9,61 все принимаем во внимание.
результат хi=9,61 все принимаем во внимание.
4. Вычисляем среднее арифметическое без учета сомнительного варианта:
 ;
;
n=10-1=9
 =9,39+9,40+9,41+9,42+9,43+9,46+9,47+9,49+9,49=84,96
=9,39+9,40+9,41+9,42+9,43+9,46+9,47+9,49+9,49=84,96

5. Находим среднеквадратическое отклонение среднего арифметического результата наблюдения по формуле
 ;
;
Разность хi – 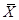
| Квадрат разности | 
|
х1- 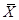 =9,39-9,44=-0,05 =9,39-9,44=-0,05
| 0,0025 | 0,0118 |
х2- 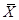 =9,40-9,44=-0,04 =9,40-9,44=-0,04
| 0,0016 | |
х3- 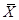 =9,41-9,44=-0,03 =9,41-9,44=-0,03
| 0,0009 | |
х4- 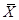 =9,42-9,44=-0,02 =9,42-9,44=-0,02
| 0,0004 | |
х5- 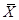 =9,43-9,44=-0,01 =9,43-9,44=-0,01
| 0,0001 | |
х6- 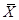 =9,46-9,44=0,02 =9,46-9,44=0,02
| 0,0004 | |
х7- 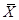 =9,47-9,44=0,03 =9,47-9,44=0,03
| 0,0009 | |
х8- 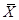 =9,49-9,44=0,05 =9,49-9,44=0,05
| 0,0025 | |
х9- 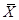 =9,49-9,44=0,05 =9,49-9,44=0,05
| 0,0025 |
Определяем число степеней свободы f=n-1=9-1=8
Рассчитываем стандартное отклонение:
 ;
;
6. Подставляем полученные расчетные данные в основную формулу (14):
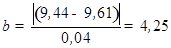 .
.
7. Находим табличное значение критерия Романовского  для n =10 и принятого уровня значимости q=0,1:
для n =10 и принятого уровня значимости q=0,1:  =2,29.
=2,29.
8. Вывод: рассчитанное значение 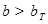 .
.
Ответ: Так как 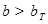 сомнительный результат наблюдения равный 9,61 является грубой погрешностью и в дальнейшей обработке полученных данных не используется.
сомнительный результат наблюдения равный 9,61 является грубой погрешностью и в дальнейшей обработке полученных данных не используется.
Пример 3.
Некоторую физическую величину измерили двумя независимыми способами. По первому способу получили результаты:38.20,38.00,37.66; по второму – 37.70,37.65,37.55. Значимо ли различаются результаты данных измерений?
Решение:
1. По формуле (6) рассчитаем среднее арифметическое значение для каждого способа:
 и
и 
2. Рассчитаем дисперсии  и
и 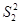
 по формуле (8):
по формуле (8):


3. Проведем сравнение точности обоих методов, используя F-распределение:
Fэксп = 
Полученные значения Fэксп, сопоставляем с табличным (табл. 6, приложения 3) значением F распределения при р=0.95 и числах степеней свободы f 1 =2 и f 2 =2.
Так как F табл= 19.00> F эксп=12.78, то расхождение между дисперсиями незначимо и, следовательно, способ измерения физической величины одинаковой точности.
С помощью t-критерия оцениваем расхождение между  и
и  . Среднее взвешенное двух дисперсий и t-критерий рассчитываем по формулам
. Среднее взвешенное двух дисперсий и t-критерий рассчитываем по формулам
|
|
|
 и
и  , тогда
, тогда

t эксп = 
Сопоставляем полученное значение t эксп с табличными t 0.95;4 = 2,776 (при р= 0,95 и f = 3+3-2=4). Так как t эксп =1.96 < t 0.95;4 = 2,776, то различие между  и
и  незначимо. Следовательно, все результаты обоих измерений отражают истинное значение физической величины.
незначимо. Следовательно, все результаты обоих измерений отражают истинное значение физической величины.
Поэтому данные измерения могут быть представлены в виде

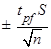 ;
;
где  – среднее арифметическое из всех n1+n2 результатов:
– среднее арифметическое из всех n1+n2 результатов:
4. Вычисляем среднее значение измерений (среднее арифметическое) по формуле (1):
 =
= 
Определим среднее квадратическое отклонение S по формуле (9):

Рассчитаем доверительные границы действительного значения результата измерения, исходя из данных наблюдений, полученных обоими способами, по формуле (15). Для расчета необходимое значение t0,95;5 находим по таблице (см. приложение 3, табл. 1)

Ответ. Результат измерений физической величины, рассчитанный по данным наблюдений полученных двумя способами, записываем следующим образом: 37.79  0,26.
0,26.
Пример 4.
При измерении некоторой величины были получены следующие результаты: 1.31, 1.45,1.42,1.32, 1.30. Опорное значение этой величины Хоп = 1,47.
Определить стандартное отклонение S, точность измерений  0.95 (
0.95 ( ,%) и сделать вывод о наличии систематической ошибки в использовании данного метода измерения.
,%) и сделать вывод о наличии систематической ошибки в использовании данного метода измерения.
Решение:
1. По формуле (6) вычисляем среднее значение измерений (среднее арифметическое):
 =
= 
2. По формуле (9) вычисляем стандартное отклонение S:
 ;
;
3.По формуле (15) рассчитываем доверительные границы случайной составляющей погрешности результата измерения. Значение коэффициента Стьюдента находим из таблицы (см. приложение 3, табл.1).

4. Покажем доверительный интервал действительного значения величины:
 ;
;

5. Точность метода обычно выражают в форме относительной погрешности, которая рассчитывается по формуле (22)

Ответ. Данный метод измерения НКПРП имеет систематическую погрешность, так как опорное значение Хоп = 1,47 не попадает в доверительный интервал 1,27  1,45. Точность измерения
1,45. Точность измерения 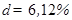 является очень низкой для данного метода.
является очень низкой для данного метода.
Пример 5.
Определить, существует ли значимое различие между выборочной средней величиной при определении НКПРП пыли обращающейся в производстве, если при отборе проб следующие результаты: 2.10, 2.12, 2.13, 2.15, 2.15 и средней генеральной совокупностью (для n =80) m =2.15 г/м3.
Решение:
1.Среднее арифметическое значение вычисляем по формуле (6):

2.Стандартное отклонение отдельного определения вычисляем по формуле (9):
 ,
,
3.Из формулы (15) находим значение величины t:

Из таблицы значений коэффициента Стьюдента (смотри таблицу 1 приложения 3) для f =4 и p =0,95, tр,f =2,78, что больше рассчитанного из формулы (15)  2,11.
2,11.
|
|
|
Ответ. Следовательно, средняя величина  не отличается значимо от средней m генеральной совокупности.
не отличается значимо от средней m генеральной совокупности.
Пример 6.
При определении коэффициента теплопроводности 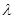 газобетона были получены результаты: 8.0×10–4 Вт/моС и 8.4×10–4 Вт/моС. Чему равна точность изменения (eр и D) коэффициента теплопроводности? Сколько параллельных измерений необходимо провести для достижения относительной точности 5%? Оправдано ли будет применение этого способа измерения для достижения такой точности?
газобетона были получены результаты: 8.0×10–4 Вт/моС и 8.4×10–4 Вт/моС. Чему равна точность изменения (eр и D) коэффициента теплопроводности? Сколько параллельных измерений необходимо провести для достижения относительной точности 5%? Оправдано ли будет применение этого способа измерения для достижения такой точности?
Решение:
1. По формуле (6) находим среднее арифметическое значение:

2.Стандартное отклонение вычисляем по формуле (9):
 ,
,
По таблице 1 приложения 3 находим для р =0.95 и f =2-1=1 tр,f =12.7 и по формуле (15) вычисляем точность метода:

3. Определяем относительную точность измерения по формуле (22):

Если необходимо получить D=5%, то
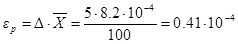 или
или 
Из формулы (15)

Если принять n =4, то t =2.90. Исходя из данных табл. 1 (см. приложение 3) для р =0.95 и f =4–1=3 tр,f =3.18, что не обеспечивает точности 5%. Если принять n =5, то t =3.24. По табл. 1 (см. приложение 3) для р =0.95 и f =5–1=4 tр,f =2.78, что меньше рассчитанного t =3.24. Следовательно, при n =5 величина t =3.24 дает большую вероятность, чем 0.95.
Ответ. Для достижения относительной погрешности 5% необходимо провести 5 измерений. Так как n <8 (n =5), то можно считать, что данный метод вполне оправдан для достижения точности 5%.
Пример 7.
Даны 93 независимых равноточных измерений некоторой физической величины.
| 75,04 | 74,96 | 75,18 | 74,82 | 75,45 | 74,55 | 75,78 | 74,22 | 76,51 | 73,49 |
| 75,05 | 74,95 | 75,19 | 74,81 | 75,46 | 74,54 | 75,79 | 74,21 | 76,52 | 73,48 |
| 75,06 | 74,94 | 75,2 | 74,8 | 75,47 | 74,53 | 75,8 | 74,2 | 76,53 | 73,47 |
| 75,07 | 74,93 | 75,21 | 74,79 | 75,48 | 74,52 | 75,81 | 74,19 | 76,54 | 73,46 |
| 75,08 | 74,92 | 75,22 | 74,78 | 75,49 | 74,51 | 75,82 | 74,18 | 76,77 | 73,23 |
| 75,09 | 74,91 | 75,23 | 74,77 | 75,5 | 74,5 | 75,83 | 74,17 | 76,78 | 73,22 |
| 75,1 | 74,9 | 75,24 | 74,76 | 75,51 | 74,49 | 75,01 | 74,99 | 75,1 | 74,9 |
| 75,11 | 74,89 | 75,25 | 74,75 | 75,52 | 74,48 | 75,02 | 74,98 | 75,11 | 74,89 |
| 75,12 | 74,88 | 75,26 | 74,74 | 74,97 | 75,03 | 75,18 | 74,82 | 75,21 | 74,79 |
| 75,13 | 74,87 |
Рассчитать:
1. При уровне значимости 0,05 исследовать предложенную выборку на однородность. Исключить все грубые ошибки с вероятностью 1-q. Найти среднее значение и эмпирический стандарт S полученной выборки.
2. Сгруппировать однородную выборку по интервалам, построить гистограмму относительных частот, сформировать гипотезу о виде распределения случайной величины Х.
3. Проверить гистограмму о распределении величины Х по критерию согласия Пирсона, установить вероятность p, с которой высказанная гипотеза не согласуется с истинным распределением. Если p<0,50, то данную гипотезу не отвергать, остановится на данном виде распределения и перейти к пункту 4. Если p>0,50, то выбрать другой закон распределения и снова применить к нему критерий согласия Пирсона. Если при исследовании гипотез о трех различных распределениях (нормальном, логарифмическом) вероятность несогласования p>0.50, то выбрать лучшее по вероятности распределения.
4. Показать, опираясь на произведенный расчет, значения среднего арифметического и стандартного отклонения (или математического ожидания и дисперсии)
Решение:
1. Исследуем данную выборку на однородность. Для этого все результаты измерений расположим в порядке возрастания. Результат запишем в виде табл. 1.
Таблица 1
Экспериментальные значения величины Х
| i | 
| i | 
| i | 
| i | 
|
| 75,04 | 74,77 | 75,03 | 75,47 | ||||
| 73,22 | 74,78 | 75,05 | 75,48 | ||||
| 73,23 | 74,79 | 75,06 | 75,49 | ||||
| 73,46 | 74,79 | 75,07 | 75,5 | ||||
| 73,47 | 74,8 | 75,08 | 75,51 | ||||
| 73,48 | 74,81 | 75,09 | 75,52 | ||||
| 73,49 | 74,82 | 75,1 | 75,78 | ||||
| 74,17 | 74,82 | 75,1 | 75,79 | ||||
| 74,18 | 74,87 | 75,11 | 75,8 | ||||
| 74,19 | 74,88 | 75,11 | 75,81 | ||||
| 74,2 | 74,89 | 75,12 | 75,82 | ||||
| 74,21 | 74,89 | 75,13 | 75,83 | ||||
| 74,22 | 74,9 | 75,18 | 76,51 | ||||
| 74,33 | 74,9 | 75,18 | 76,52 | ||||
| 74,48 | 74,91 | 75,19 | 76,53 | ||||
| 74,49 | 74,92 | 75,2 | 76,54 | ||||
| 74,5 | 74,93 | 75,21 | 76,77 | ||||
| 74,51 | 74,94 | 75,21 | 76,78 | ||||
| 74,52 | 74,95 | 75,22 | |||||
| 74,53 | 74,96 | 75,23 | |||||
| 74,54 | 74,97 | 75,24 | |||||
| 74,55 | 74,98 | 75,25 | |||||
| 74,74 | 74,99 | 75,26 | |||||
| 74,75 | 75,01 | 75,45 | |||||
| 74,76 | 75,02 | 75,46 |
По условию требуется проверить, не содержит ли данная выборка грубых погрешностей на уровне значимости 0.05,это значит из выборки следует исключить те хi, которые с вероятностью 1– q =0.95 являются грубой погрешностью.
Найдем критическое значение числа, с которым будем сравнивать максимальное отклонение t (xi):
 ,
,
Примечание. Практические исследования показали, что при n  6, отбраковку данных производить не следует. Если 6<n
6, отбраковку данных производить не следует. Если 6<n  100, то используется предлагаемый подход. При 100<n
100, то используется предлагаемый подход. При 100<n  1000 максимальное относительное отклонение сравнивают с K=3 и при n>1000 – с К=2,5 для всех уровней значимости.
1000 максимальное относительное отклонение сравнивают с K=3 и при n>1000 – с К=2,5 для всех уровней значимости.
Для наглядности нанесем на график все значения из табл. 1.
Рисунок 1 
Как можно видеть из рис., наиболее густо точки расположены в интервале [73-77]. Значительных отклонений крайних значений не наблюдается, но, тем не менее, для исключения ошибки при обработке полученных данных необходимо проанализировать результаты на наличие грубой погрешности. Многие делают ошибку, ставя под сомнение самые крайние значения в вариационном ряду. Необходимо выявить те значения, которые в большей мере отличаются от основного массива данных, даже если после них присутствуют другие значения. Если же возьмем для анализа крайние значения, упустив из внимания близлежащие к ним, то разность между основным массивом и крайним значением при обработке будет увеличена, так как мы упускаем из внимания, а, следовательно, и из обработки указанные близлежащие значения. В нашем случае к таким данным мы можем отнести результаты x 1=73,22, x 2=73,23. Также можно рассуждать в отношение x 92- x 93. Начать анализ указанных данных на грубую погрешность можно с тех значений, которые в наибольшей степени отличаются от соседнего значения. К таким относятся x 2 и x 90. Если эти значения будут являться грубыми погрешностями, тогда и остальные (x 1, x 93) также следует в дальнейшем исключать из обработки или рассматривать их как отдельные ряды и учитывать это в применяемых расчетных формулах.
Проанализируем значение x 2=73,23. Для этого найдем среднее арифметическое значение и стандартное отклонение для выборки из 89 чисел, т.е. не включаем в выборку сомнительный вариант x 2=73,22, а также x 1, x92, x 93.
Среднее арифметическое значение находиться по формуле:

где 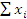 - это сумма i-тых значений; а n- это количество значений.
- это сумма i-тых значений; а n- это количество значений.
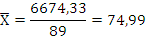
Стандартное отклонение находиться по формуле:
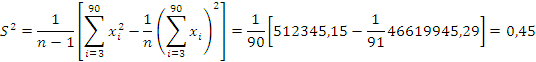
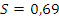
Итак, мы нашли среднее арифметическое значение и стандартное отклонение, теперь начинаем исследовать значение x 2=73,23. Для этого подставим наши значения в формулу  , и тогда мы получим:
, и тогда мы получим: 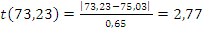 . Теперь полученное значение сравниваем с критическом отклонением и получаем, что
. Теперь полученное значение сравниваем с критическом отклонением и получаем, что  . А это означает, что значение x 2=73,23 не несет в себе грубую погрешность, и следовательно оно не исключено из последующей обработки, это же суждение распространяется на x 1. Таким же образом, исследуем значение x92 =76,77.
. А это означает, что значение x 2=73,23 не несет в себе грубую погрешность, и следовательно оно не исключено из последующей обработки, это же суждение распространяется на x 1. Таким же образом, исследуем значение x92 =76,77.  , полученное значение сравниваем с критическим отклонением
, полученное значение сравниваем с критическим отклонением 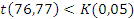 . Из этого следует, что значения x92,x 93 так же не несут в себе грубую погрешность и не должны исключаться из дальнейшей обработки.
. Из этого следует, что значения x92,x 93 так же не несут в себе грубую погрешность и не должны исключаться из дальнейшей обработки.
При заданной вероятности 1– q =0.95 выборка, представленная в табл.1, является однородной.
Для полученной выборки находим
 ;
;  ;
; 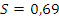
2. Сгруппируем данные табл. 1 по интервалам. Для хорошей статистики считается оптимальным число интервалов C=  , где n - число измерений, так же число интервалов приближенно можно рассчитать по формуле Стерджеcса
, где n - число измерений, так же число интервалов приближенно можно рассчитать по формуле Стерджеcса 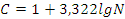 , в данном примере используем первую формулу (для своего контроля можно использовать обе формулы). Ширину интервала (шаг) вычисляем по соотношению
, в данном примере используем первую формулу (для своего контроля можно использовать обе формулы). Ширину интервала (шаг) вычисляем по соотношению  .
.
Подставляем наши значения и получаем:


Найденное значение ширины интервалов можно округлять. Обычно округление производится в сторону увеличения, чтобы не уменьшать общий диапазон варьирования значения.
Найдем границы интервалов  , (где i – номер интервала) включающих все данные табл. 1, а также подсчитаем, сколько значений величины Х попадает в каждый интервал, то есть найдем частоты ni.
, (где i – номер интервала) включающих все данные табл. 1, а также подсчитаем, сколько значений величины Х попадает в каждый интервал, то есть найдем частоты ni.
Нижняя граница первого интервала выбирается так, чтобы минимальные варианты выборки  попадало примерно в середину этого интервала. Начальную точку рассчитываем, в соответствии с уравнением. Отсюда нижняя граница первого интервала определяется как
попадало примерно в середину этого интервала. Начальную точку рассчитываем, в соответствии с уравнением. Отсюда нижняя граница первого интервала определяется как  . Для нашего примера
. Для нашего примера  . Прибавив к этой величине ширину интервала, найдем нижнюю границу второго интервала
. Прибавив к этой величине ширину интервала, найдем нижнюю границу второго интервала 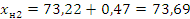 Это будет одновременно и верхняя граница
Это будет одновременно и верхняя граница 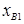 предыдущего (первого) интервала. После того как намечены границы всех интервалов, остается распределить по этим интервалам полученные данные измерений. Однако при этом возникает следующий вопрос: как поступать в тех случаях, если какое-либо значение из наших данных попадает точно на границу соседних интервалов группировки, т.е. результат совпадает с нижней границей одного и верхней границей соседнего с ним интервала? Такие данные могут быть с одинаковыми основаниями отнесены к любому из соседних интервалов, и, чтобы исключить неопределенность такой ситуации, уменьшим верхние границы всех интервалов на величину, равную точности измерения признака (обычно задается при постановке целей измерения, например, произвести измерение с точностью
предыдущего (первого) интервала. После того как намечены границы всех интервалов, остается распределить по этим интервалам полученные данные измерений. Однако при этом возникает следующий вопрос: как поступать в тех случаях, если какое-либо значение из наших данных попадает точно на границу соседних интервалов группировки, т.е. результат совпадает с нижней границей одного и верхней границей соседнего с ним интервала? Такие данные могут быть с одинаковыми основаниями отнесены к любому из соседних интервалов, и, чтобы исключить неопределенность такой ситуации, уменьшим верхние границы всех интервалов на величину, равную точности измерения признака (обычно задается при постановке целей измерения, например, произвести измерение с точностью  ).
).
Для удобства последующей обработки сгруппированных данных вычислим срединные значения интервалов группировки  , которые отстоят от нижних границ на величину, равную половине ширины интервалов, т.е.
, которые отстоят от нижних границ на величину, равную половине ширины интервалов, т.е.  .
.
Результаты запишем в табл. 2.
Таблица 2
| i | Границы интервалов | Средние значения | Частота попаданий в i- ый интервал (ni) | 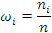
| 
|
| 72,99-73,46 73,46-73,93 73,93-74,40 74,40-74,87 74,87-75,34 75,34-75,81 75,81-76,28 76,28-76,75 76,75-77,22 | 73,22 73,70 74,17 74,64 75,11 75,58 76,05 76,52 76,99 | 0,032 0,032 0,075 0,215 0,430 0,129 0,022 0,043 0,022 | 0,069 0,069 0,160 0,458 0,915 0,275 0,046 0,092 0,046 |
По полученным данным построим гистограмму.
Рисунок 2

|
|
|


