Главная | Обратная связь | Поможем написать вашу работу!

Проверка гипотезы о логарифмически нормальном распределении

величины Х

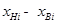
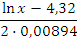
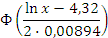
i Границы интервалов p_i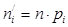

72,99-73,46 73,46-73,93 73,93-74,40 74,40-74,87 74,87-75,34 75,34-75,81 75,81-76,28 76,28-76,75 76,75-77,22 - -1,3008 -0,9441 -0,5897 -0,2375 0,1125 0,4603 0,8060 1,1495 + -0,5000 -0,4032 -0,3264 -0,2190 -0,0910 0,0438 0,1772 0,2881 0,3749 +0,5000 0.0968 0.0768 0.1074 0.1280 0.1348 0.1334 0.1109 0.0868 0.1251 9,00 7,14 9,99 11,90 12,54 12,41 10,31 8,07 11,63

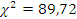
Как можно видеть, значение критерия 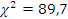велико, следовательно, логарифмически нормальное распределение отклоняется.

Поскольку распределение величины Х не является нормальным, но число опытов достаточно велико (n=93>30).

При подборе распределения величины Х значение p . Исходя из этого, принимаем, что величина q=0.01. По «Значения функции Лапласа Ф(х)» аргумента 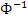соответствует значению функции Ф(0,495)=0,1897, тогда .

Тогда:

и

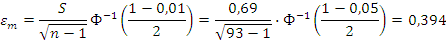
И с вероятностью приблизительно 0,99 имеем математическое ожидание в интервале 75,016<m<75,044, а так же рассеяние(дисперсию) в интервале 0,296<у<1,084.

Пример 8.

С помощью тестера (мультиметра), работающего в режиме измерения переменного напряжения, получено значение U_изм=120 В. Диапазон измерений прибора от 0 до 50 В. В паспорте указано, что при работе в этом диапазоне относительная погрешность не превышает двух процентов. Записать результат измерения.

Решение:

1. Результат измерения обычно записывается в форме: Х_д=Х_изм+ Х; для нашего случая эта запись будет иметь вид:

U_д= U_изм+ U, при относительной погрешности ,

где U_изм – измеренное значение (120 В); U – абсолютная погрешность измерения; - относительная погрешность (2%).

2. Абсолютная погрешность определяется из формулы:

, откуда

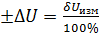
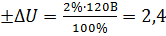В.

Ответ: Результат измерения записывается в виде U = (120,0 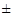2,4 В) при = 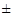2 %. Запись 120,0 применяется, исходя из записи погрешности, имеющей знак после запятой (2,4). Поэтому при записи результата измерения это учитывается.

Пример 9.

Для выполнения измерений применялось средство измерения с классом точности 2,5, со шкалой, проградуированной от 0 до 5 и ценой деления 0,2. Было получено значение величины A=3. Записать результат измерения.

Решение:

1. Результат измерения записывается обычно в форме

А_д=А_изм 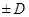А при относительной погрешности ,%, где А_изм – измеренное значение величины, А – абсолютная погрешность, относительная погрешность.

Для решения задачи вспомним обозначение погрешностей через класс точности измерительного прибора.

2. Если класс точности обозначим 2,5, это означает, что приведенная погрешность 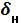= 2,5%.

Воспользуемся формулой приведенной погрешности:

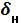=ΔА/А_н*100%,

где: А_н – ширина диапазона измерений.

Из этой формулы следует, что:

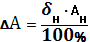, тогда

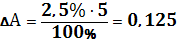Относительная погрешность измерения рассчитывается по формуле:

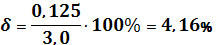Ответ: Результат измерения запишем А_д=(3,000 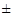0,125) при относительной погрешности .

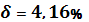Число знаков после запятой в записи результата и погрешности должно быть одинаково.

Пример 10.

Для выполнения измерений применялось средство измерения с классом точности , со шкалой, проградуированной от 0 до 10 и ценой деления 0,2. Было получено значение величины A=4. Записать результат измерения.

Решение:

Решение задачи осуществляется аналогично примеру 9.

1. Если класс точности обозначается , это значит, что относительная погрешность =5,0%. Тогда

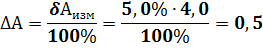
Ответ: Результат измерения запишется как А=4,0 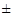0,5 при =5,0%.

Пример 11.

Для выполнения измерений применялось средство измерения с классом точности 2,5/1,0, со шкалой, проградуированной от 0 до 10 и ценой деления 0,2. Было получено значение величины A=6. Записать результат измерения.

Решение:

1. Если класс точности обозначается 2,5/1,0, это значит, что указаны приведенные погрешности в конце и в начале диапазона измерений соответственно: 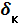=2,5%, 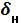=1,0%.

Для расчета относительной погрешности результата измерения используется формула

, т.е.

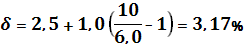2. Рассчитываем абсолютную погрешность измерения

(единицы измерения)

Ответ: Результат измерения запишется как А=6,00 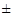0,19 при =3,17%.

Примечание.

Если будем иметь данное не об одном, а о нескольких результатах наблюдения одной и той же величины, полученных с использованием одного и того же средства измерения, то следует вначале определить среднее арифметическое значение, которое и будет приниматься за измеренное значение.

Пример 12.

При определении значимости характеристик объекта экспертным методом мнения экспертов сложились следующим образом:

№1	-	Q₁	Q₂	Q₃	Q₄	Q₅	Q₆ Q₅ Q₅ Q₆ Q₅
№2	-	Q₂	Q₃	Q₁	Q₆	Q₄
№3	-	Q₁	Q₂	Q₄	Q₆	Q₃
№4	-	Q₁	Q₃	Q₂	Q₅	Q₄
№5	-	Q₂	Q₄	Q₁	Q₆	Q₃

Необходимо определить степень согласованности мнения пяти экспертов

Решение:

Для решения используем формулу:

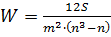где: W – коэффициент конкордации;

S – сумма квадратов отклонений всех оценок рангов для каждого объекта экспертизы от среднего значения;

m – число экспертов;

n – число объектов экспертизы.

0<W<1

При W=0 – полная несогласованность

W=1 – полное единодушие.

Для удобства обработки результатов все расчетные данные следует свести в таблицу:

№ объекта экспертизы	Оценка эксперта	сумма рангов	Qср.	Отклонение от среднего	Квадрат отклонения	Сумма квадратов отклонений (S)	12S	m²	n³	n³-n	W

							17,5	10,5	110,25	351,5		0,8
							3,5	12,25
							6,5	42,25
							9,5	90,25
							2,5	6,25
							9,5	90,25

Ответ: Мнения экспертов согласованы в достаточной мере. Обработку данных можно проводить дальше.

Пример 13.

Дать характеристику документу по стандартизации (ГОСТ 30402-96 Материалы строительные. Метод испытания на воспламеняемость) в соответствии с указанным ниже планом:

1. Полное наименование документа;

2. Вид документа (тип);

3. Дать определение названного документа;

4. Уровень разработки документа;

5. Общий объект стандартизации;

6. Объект стандартизации конкретного документа;

7. Назначение документа;

8. Область применения;

9. Дата введения в действие;

10. Структура документа;

11. Наличие изменений и дополнений;

12. Наличие ссылок на другие документы;

13. Для стандартов указать категорию и вид;

14. Характер применения документа;

1. ГОСТ 30402-96 Материалы строительные. Метод испытания на воспламеняемость.

2. Стандарт.

3. Стандарт – документ, в котором в целях добровольного и многократного использования устанавливается характеристики продукции, правила осуществления и характеристики процессов производства, эксплуатации, хранения, перевозки, реализации, утилизации выполнения работ или оказания слуг. Стандарт может также содержать требования к терминологии, символики, упаковке, маркировке или этикеткам и правилам их нанесения.

4.Уровень разработки данного нормативного документа – Государственный центральный научно-исследовательский и проектно-экспериментальный институт комплексных проблем строительных конструкций и сооружений имени В.А.Кучеренко (ЦНИИСК им.Кучеренко) Государственного научного центра «Строительство» (ГНЦ «Строительство») Минстроя России совместно с Всероссийским научно-исследовательским институтом противопожарной обороны (ВНИИПО) МВД России и Центром противопожарных исследований и тепловой защиты в строительстве ЦНИИСК (ЦПИТЗС ЦНИИСК)

5. Общим объектом стандартизации является строительство.

6.Объектом стандартизации являются воспламеняемые строительные материалы в рамках метода испытания на воспламеняемость.

7. Настоящий стандарт устанавливает метод испытания строительных материалов на воспламеняемость и классификацию их по группам воспламеняемости.

8. Настоящий стандарт применяется для всех однородных и слоистых горючих строительных материалов.

9. Введен в действие с 01.07.96 г.

10. Структура нормативного документа:

Введение

1. Область применения

2. Нормативные ссылки

3. Определения

4. Основные положения

5. Классификация строительных материалов по группам воспламеняемости

6. Образцы для испытания

7. Оборудование для испытания

7.1. Общие положения

7.2. Опорная станина

7.3. Радиационная панель

7.4. Система зажигания

7.5. Вспомогательное оборудование

8. Калибровка установки

8.1. Общие положения

8.2. Порядок проведения калибровки

9. Проведение испытания

10. Протокол испытания

11. Требования безопасности

Приложения

11. -

12. В настоящем стандарте использованы ссылки на следующие нормативные документы:

ГОСТ 12.005-88 ССБТ. Общие санитарно-гигиенические требования к воздуху рабочей зоны;

ГОСТ 12.1.019-79 ССБТ. Электробезопасность. Общие требования и номенклатура видов защиты;

ГОСТ 18124-95 Листы асбестоцементные плоские;

ГОСТ 30244-94 Материалы строительные. Методы испытания на горючесть;

СТ СЭВ 383-87 Пожарная безопасность в строительстве. Термины и определения.

13. Категория стандарта – межгосударственный стандарт

Вид нормативного документа - стандарт на методы контроля (испытаний).

14. Данный документ имеет добровольный характер применения.

Пример 14.

Оцените годность пружинного манометра класса точности 1,0 на 60 кПа, если при его поверке методом сличения с образцовым манометром класса точности 0,2 в точке 50 кПа при повышении давления было зафиксировано 49,5 кПа, а при понижении 50,2 кПа.

Решение:

Вариация показаний пружинного манометра не должна превышать основной погрешности. В нашем случае манометр класса точности 1,0 может иметь абсолютную погрешность 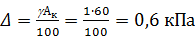. Это же значение может иметь и вариация показаний b. Для нашего манометра:

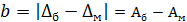
где: 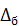и 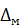- абсолютная погрешность при подходе к поверяемой точке со стороны больших и меньших значений, соответственно; 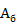и 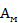— показания образцового прибора в этих точках, т.е.

Следовательно, b>Д, так как 0,7 кПа > 0,6 кПа.

Манометр должен быть забракован, несмотря на то, что погрешности в точке 50 кПа не превышают допускаемую: (0,2 < 0,6 и 0,5 < 0,6).

Пример 15.

Как выразится единица электрического напряжения (вольт, В) через основные единицы системы СИ?

Решение. Воспользуемся следующим уравнением для напряжения 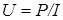, где Р – мощность, выделяющаяся на участке цепи при протекании в ней тока I. Следовательно, 1 В – это электрическое напряжение, вызывающее в электрической цепи постоянный ток силой в 1 А при мощности в 1 Вт. Дальнейшие преобразования:

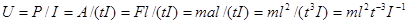
Таким образом, получим соотношение, в котором все величины выражаются через основные единицы системы СИ. Следовательно, .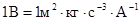

Пример 16.

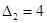Погрешность результата измерения напряжения распределена равномерно в интервале от В до В.

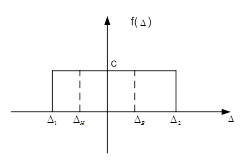
Рис. 1.

Найдите систематическую погрешность результата измерения, среднюю квадратическую погрешность и вероятность того, что погрешность результата измерения лежит в пределах от 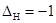В до 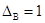В (рис. 1).

Решение.

Систематическая погрешность равна математическому ожиданию, которое для равномерного закона распределения определяется формулой:

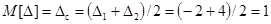В.

Средняя квадратическая погрешность определяется формулой:

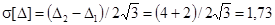В.

Вероятность попадания погрешности в заданный интервал определяется из соотношения:

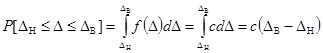где - высота закона распределений.

Следовательно,

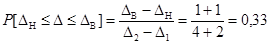8. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ

Единица физической величины – это физическая величина фиксированного размера, которой условно присвоено числовое значение, равное единице.

Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств.

Результат измерений – значение характеристики, полученное выполнением регламентированного метода измерений. В простейшем случае результат измерений (испытаний) является собственно наблюдаемым значением.

Единство измерений – состояние измерений, при котором их результаты выражены в указанных единицах, а погрешности известны с заданной вероятностью и не выходят за установленные пределы.

Достоверность – степень соответствия среднего значения, полученного в ходе проведения большого числа наблюдений, опорному значению. Достоверность измерений – это близость к нулю случайной или (неисключенной) систематической погрешности.

Повторяемость (сходимость) – степень совпадения наблюдаемых значений или результатов независимых испытаний, полученных при заданных условиях на идентичных установках в одной лаборатории.

Воспроизводимость – степень совпадения наблюдаемых значений или результатов независимых испытаний полученных при заданных условиях на идентичных установках в различных лабораториях.

Точность – это близость результатов измерений к принятому опорному значению.

Правильность – степень близости среднего значения, полученного на основании большой серии результатов измерений (испытаний), к принятому опорному значению.

Прецизионность – степень близости друг к другу независимых результатов измерений, полученных в конкретных регламентированных условиях. Прецизионность зависит только от случайной составляющей погрешности и не имеет отношения к опорному значению измеряемой величины.

Воспроизводимость результатов – характеристика результатов испытаний, определяемая близостью результатов повторных испытаний объекта.

Выброс (промах) – наблюдения в выборке, настолько отличающееся по своим значениям от остальных, что напрашивается предположение об их принадлежности к другой совокупности или неправильном выборе метода статистического анализа. Согласно ГОСТ Р ИСО 5725-1-2002, выбросом называется элемент совокупности значений, который несовместим с остальными элементами данной совокупности.

Погрешностью называют отклонение результата измерений от опорного значения измеряемой величины. При этом следует иметь в виду, что опорное значение физической величины считается неизвестным и применяется в теоретических исследованиях, а действительное значение устанавливается экспериментальным путём в предположении, что результат эксперимента (измерения) в максимальной степени приближается к опорному значению. Погрешности измерений приводятся обычно в технической документации на средства измерений или в нормативных документах.

Погрешность измерений – это отклонение результата измерений от опорного значения измеряемой величины. При измерениях получить опорное значение измеряемой величины невозможно, т.к. в результате любого познавательного процесса невозможно получить абсолютную истину. Поэтому результату любого измерения всегда присуща погрешность.

Случайная составляющая погрешности – это составляющая погрешности, изменяющаяся случайным образом при измерениях одной и той же величины. Случайная составляющая вызывает вариацию (разброс) результатов.

Систематическая составляющая погрешность (смещение) – это разность между математическим ожиданием результатов измерений и опорным значением. Если математическое ожидание систематической погрешности известно и постоянно, то в результате измерений вносят соответствующую поправку. Знак поправки противоположен знаку погрешности. Систематическая составляющая погрешности устойчиво искажает (смещает) результаты измерений.

Грубая погрешность – погрешность, которая явно и резко искажает результаты измерений. Они обычно исключаются из результата наблюдения (это неправильный отсчёт по шкале, неправильная запись в журнале). Грубые погрешности, как правило, возникают при однократных измерениях и обычно устраняются путём повторных измерений.

Многократные измерения – измерения одного и того же размера физической величины следующие друг за другом, проводящиеся с целью уменьшения случайной составляющей погрешности.

Генеральная совокупность – группа множеств (совокупностей), часто отражающая различные характеристики рассматриваемых изделий (объектов или материалов).

Доверительный интервал – интервал, которой с заданной вероятностью накроет неизвестное значение оцениваемого параметра, распределения.

Доверительная вероятность – вероятность того, что доверительный интервал накроет действительное значение параметра оцениваемого по выборочным данным.

⇐ Предыдущая 4 5 6 7 8 9 10 111213 Следующая ⇒

Воспользуйтесь поиском по сайту: