Функции законов распределения

Нормальный закон распределения занимает особое место среди других законов распределения измеряемых величин, рассматриваемых как случайные величины, и является предельным. К нему при некоторых ограничениях сходится сумма большого числа независимых случайных величин, подчиненных любым законам распределения, при условии, что каждая из величин в сумме не имеет превалирующего влияния.

Реальные законы распределения результатов и погрешностей измерений часто отличаются от нормального, особенно после эксплуатации средств измерений свыше 3…5 лет, когда сказываются процессы старения в узлах и элементах средств измерений. Поэтому при выполнении точных измерений всегда целесообразно изучить реальную форму закона распределения результатов измерений и учитывать его свойства при обработке этих результатов. Поскольку погрешности искажают эмпирический закон распределения вероятности результата измерений, постольку проверка предположения о его нормальности производится после исключения погрешностей (грубых и систематических – определяемых и исключаемых, исходя из возможностей).

Нормальный закон распределения величины Х представляется плотностью распределения

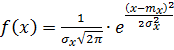; (35)

где: m_x – математическое ожидание величины Х; 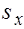- среднее квадратическое отклонение (теоретическое); f(x) – плотность распределения вероятностей (дифференциальная функция распределения, описывающая результат измерения).

В отношении описания случайных погрешностей измерений данная функция обозначается f (). Дифференциальная функция распределения – производная от интегральной по своему аргументу:

; . (36)

Графики дифференциальных функций распределения (рис. 4) называют также кривыми распределения, в ряде случаев они имеют колоколообразную форму и обладают максимумом при х=х _ист или =0 соответственно.

Рис. 4. График дифференциальных функций распределения

 

Под интегральной функцией распределения результатов измерений (рис. 5) понимают вероятность того, что результат измерения Х в i-м опыте окажется меньше некоторого текущего значения х, т.е.

. (37)

Рис. 5. Интегральная функция распределения результатов измерений

 

Случайную погрешность рассматривают как случайную величину, принимающую различные значения _i. Ее интегральную функцию распределения получают путем переноса начала координат в точку х=х _ист

. (38)

При переходе от дифференциальной функции распределения к интегральной путем интегрирования получают

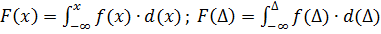. (39)

Предполагая в соответствии с теорией вероятностей, что =1, получают

, (40)

т.е. площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс, равна единице.

При проведении измерения вероятность попадания результата измерения Х или случайной погрешности в интервал (х₁; х₂) или ( ₁; ₂) оценивают по формулам:

; (41)

(42)

или в обозначениях дифференциальной функции распределения:

; (43)

. (44)

Таким образом, вероятность попадания результата измерения или случайной погрешности в заданный интервал равна площади, ограниченной кривой распределения, осью абсцисс и перпендикулярами к ней на границах этого интервала (заштрихованная площадь на рис 3.6.1.1). Произведения f(x) d(x) и f( ) d( ) называются элементами вероятности и равны вероятности того, что случайные величины Х и примут некоторые значения в интервалах d(x) и d( ) соответственно. Формы кривой распределения позволяют судить о том, какие интервалы значений более, а какие менее вероятны. Закон распределения и его характеристики значений Х или погрешности дают исчерпывающую информацию о случайных величинах Х и . На практике зачастую достаточно знать только числовые характеристики законов распределения.

Результаты измерений в значительной степени сконцентрированы вокруг истинного (действительного) значения измеряемой величины, и по мере приближения к нему элементы вероятности их появления возрастают. Характеристикой центра группирования случайной величины является математическое ожидание. Математическое ожидание (М(Х) или М(), где Х – результат измерений, - погрешность результата измерения) не определяет степень рассеяния возможных значений около среднего значения.

Для оценки свойств законов распределения и полной характеристики распределения результата измерения Х или погрешности измерения применяют числовые характеристики, называемые моментами. Различают начальные моменты (числовые характеристики, найденные без исключения систематической составляющей) и центральные моменты.

Центральные моменты характеризуют случайную величину (погрешность) за вычетом систематической составляющей, т.е. они становится центрированными. Таким образом, случайная составляющая погрешности измерения – это центрированная величина.

Часто применяется центральный момент второго порядка, который получил наименование дисперсии. Дисперсия характеризует рассеяние случайной величины относительно ее математического ожидания. В практических задачах рассеяние чаще характеризуют средним квадратическим отклонением , так как оно имеет одну и ту же размерность, что и случайная величина. Дисперсии распределения результатов и случайных погрешностей измерения имеют значения, равные квадрату измеряемой величины

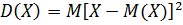; . (45)

Для более подробного описания распределения используют моменты более высоких порядков.

Центральные и начальные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов измерений, так как математическое ожидание случайных погрешностей равно нулю.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: