 |
Подбор функции (закона) распределения случайной величины
|
|
|
|
Для изучения закона распределения случайной величины Х (экспериментальные данные) полезно построить гистограмму относительных частот. Наглядность отображения гистограммой закона распределения вероятности зависит от соблюдения следующих правил при ее построении:
1)интервалы 
х, на которые разбивается ось абсцисс, следует выбирать, по возможности, одинаковыми;
2)число интервалов k устанавливать в соответствии со следующими рекомендациями:
| Число измерений (n) | Рекомендуемое число интервалов (k) |
| 40-100 | 7-9 |
| 100-200 | 15-18 |
| 18-20 | |
| 25-30 | |
| 35-40 |
3)масштаб выбирать таким, чтобы высота гистограммы относилась к основанию примерно, как 5 к 8.
Вся область изменения экспериментальных данных разбивается на интервалы, оптимальная длина которых
 или  ,
| (46) |
а начальная точка отсчета
 .
| (47) |
Заметим, что в большинстве случаев все значения Х должны быть положительны (распределение Вейбулла, логарифмически нормальное распределение и др.), поэтому в таких случаях, если х0<0, принимают х0=0.
На практике эти формулы используют не всегда, так как длина интервала определяется естественно, в зависимости от точности прибора, с помощью которого производится измерение величины Х. Далее находят границы интервалов и подсчитывают количество значений xi, попавших в каждый интервал, которое принимается за частоту ni попадания величины Х в заданный интервал. Если при этом граница интервала совпадает с одним из значений xi, то к частотам для каждого интервала подсчитывают относительную - частоту
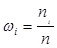. (48)
Гистограмма относительных частот (рис. 6) – это ступенчатая фигура, состоящая из прямоугольников с основаниями hx и высоты wi/hx. Число wi/hx называют плотностью относительных частот. Отметим, что площадь гистограммы (всех построенных прямоугольников) равна 1, поскольку в нее входят все 100% наблюдений.
|
|
|
Соединив отрезками прямых середины верхних сторон прямоугольников, получим ломаную линию, называемую полигоном. Если бы была возможность увеличивать число измерений n, то в пределе при n 
и 
0 (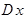
- цена деления шкалы прибора) полигон перешел бы в кривую плотности распределения f(x). Нормальное распределение имеет симметричную кривую плотности вероятности, поэтому и гистограмма должна представлять собой симметричную фигуру.
Если максимум на гистограмме сдвинут к нулю, то следует предполагать логарифмически нормальное распределение или распределение Вейбулла. По виду гистограммы эти законы трудно различить; можно лишь обратить внимание на то, что гистограмма при логарифмически нормальном распределении плотнее примыкает к оси ординат.
Возможно, что случайная величина, гистограмма которой изображена на рис. 7, распределена по логарифмически нормальному закону, а на рис. 8 – по закону Вейбулла.
Для идентификации неизвестного закона распределения возможных значений измеряемой величины используют так называемые критерии согласия. Известны несколько критериев согласия. В зависимости от применяемых критериев согласия закон распределения представляется в виде плотности распределения, функции распределения или отношений центральных моментов случайной величины.
Наиболее часто на практике используется критерий согласия Пирсона (хи-квадрат,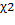 
), который можно применять для проверки допущения о любом распределении, даже не зная точного значения параметров распределения. Основным недостатком этого критерия является нечувствительность к обнаружению подходящей статистической модели при малом числе наблюдений.
3.6.3. Применение критерия согласия Пирсона
|
|
|
При использовании этого критерия замеры расхождения экспериментальных данных с теоретическим законом распределения вероятности результата измерения (вероятность Р есть вероятность того, что за счет чисто случайных причин мере расхождения теоретического и эмпирического распределения должна быть не меньше, чем полученное по результатам измерений) принимается сумма квадратов отклонения частностей mi/n от теоретической вероятности Рi попадания отдельного значения результата наблюдения в i-й интервал, причем, каждое слагаемое берется с коэффициентом n/Pi:
, (49)
Если расхождение случайно, то 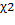подчиняется 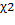- распределению.
Пусть произведено n независимых измерений некоторой величины Х, рассматриваемой как случайная. Задавшись значением интегральной функции распределения К. Пирсона F(
), можно проверить больше или меньше ее аргумента вычисленное значение 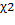. Если меньше, то с выбранной вероятностью (Рi) 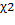можно считать случайным числом, подчиняющимся 
- распределению К. Пирсона, т.е. признать случайным расхождение между эмпирической (опытной) и теоретической плотностью распределения вероятности результата измерения.
Если же окажется, что 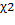больше чем 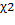, то с той же вероятностью придется признать, что 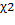не подчиняется распределению К. Пирсона, т.е. гипотеза о соответствии эмпирического закона распределения вероятности теоретическому не подтверждается.
При проверке нормальности закона распределения вероятности результата измерения применение критерия согласия 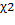дает хорошие результаты только, если n>40…50. При меньшем числе наблюдений применяется так называемый составной критерий.
Результаты наблюдений случайной величины х, полученные в специально поставленном эксперименте, или на основании сбора статистических данных, представляют в виде ранжированного ряда – последовательности измеренных значений величины, расположенных в порядке возрастания от наименьшего до наибольшего х1 <х2 <….< хn. При этом наблюдения случайной величины X должны проводиться в практически одинаковых условиях, а исследуемая совокупность должна быть однородной.
Целесообразен следующий порядок работы:
1. Найти точечные оценки неизвестных параметров принятого распределения.
|
|
|
2. Подсчитать теоретическую вероятность pi показания случайной величины в i-ом интервале по формуле
 ,
| (50) |
где: xi и xi+1 – границы i-ого интервала; 
– теоретическая функция распределения.
3. Вычислить теоретическую частоту (число наблюдений) для каждого интервала по формуле:
 ,
| (51) |
где: 
– общее число наблюдений (объем однородной выборки); 
– теоретическая вероятность i-ого интервала.
4. Условия применения критерия Пирсона требуют, чтобы ожидаемое (теоретическое) число наблюдений для каждого интервала было не менее 5. Если в каком-либо интервале окажется 
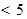, то его нужно объединить с соседним интервалом (или интервалами) таким образом, чтобы суммарная теоретическая частота была не менее 5.
5. Вычислить критерий Пирсона:
 ,
| (52) |
где: 
и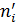 
– соответственно фактическое и ожидаемое числа значений случайной величины, попадающих в i-ый интервал; k – число интервалов, полученное после объединения по пункту 4.
6. Подсчитать число степеней свободы:
 ,
| (53) |
где: k – число интервалов, для которых 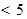; r – число параметров распределения F(x), для которых точечные оценки были найдены по данным выборки в п.1.
7. Сравнить полученное значение 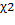с критическими значениями квантилей распределения Пирсона, соответствующими полученному числу степеней свободы f (см. табл. 4 приложения 3).
Пусть 
, где 
и 
– квантили из табл. 4 приложения 3, которые соответствуют вероятностям q1 и q2. Тогда с вероятностью qÎ[q1, q2] гипотеза о предполагаемом распределении с интегральной функцией F(x) не согласуется с истинным распределением. Если числа q1 и q2 малы, то выбранный закон не противоречит имеющимся данным с большой надежностью 1–qÎ[1–q1, 1–q2]. При больших 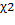(и q велико) вероятность, что гипотеза верна, то есть 1–q, близка к нулю и требуется дальнейшее исследование заданной выборки.
|
|
|
