 |
Подбор функции (закона) распределения случайной величины.
|
|
|
|
Для изучения закона распределения случайной величины Х (экспериментальные данные) полезно построить гистограмму относительных частот. Наглядность отображения гистограммой закона распределения вероятности зависит от соблюдения следующих правил при ее построении:
4)интервалы  х, на которые разбивается ось абсцисс, следует выбирать, по возможности, одинаковыми;
х, на которые разбивается ось абсцисс, следует выбирать, по возможности, одинаковыми;
5)число интервалов k устанавливать в соответствии со следующими рекомендациями:
| Число измерений (n) | Рекомендуемое число интервалов (k) |
| 40-100 | 7-9 |
| 100-200 | 15-18 |
| 18-20 | |
| 25-30 | |
| 35-40 |
6)масштаб выбирать таким, чтобы высота гистограммы относилась к основанию примерно, как 5 к 8.
Вся область изменения экспериментальных данных разбивается на интервалы, оптимальная длина которых:
 или или  , ,
|
а начальная точка отсчета:
 . .
|
Заметим, что в большинстве случаев все значения Х должны быть положительны (распределение Вейбулла, логарифмически нормальное распределение и др.), поэтому в таких случаях, если х0<0, принимают х0=0.
Предположим, что случайная величина распределена по нормальному закону распределения с параметрами  и
и 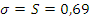 . Гипотезу о нормальном распределении случайной величины Х проверим по критерию согласия Пирсона. Результаты вычислений занесем в табл. 3.
. Гипотезу о нормальном распределении случайной величины Х проверим по критерию согласия Пирсона. Результаты вычислений занесем в табл. 3.
Для заполнения табл. 3 в столбец 2 занесем из табл. 2 (нашего примера) граничные значения интервалов xi; затем заполняем столбец 3 по формуле  , где
, где  -начальная граница интервала. Следующий столбец нахождение значения функции Лапласа по данным таблицы «Значения функции Лапласа Ф(х)», используя при необходимости линейное интерполирование. Считаем при x 0= –¥ и x 9= +¥. Теоретическую вероятность (столбец 5) находим по формуле pi=F(x i+1)-F(x i) и записываем результаты между строк столбца 4. Затем вычисляем
-начальная граница интервала. Следующий столбец нахождение значения функции Лапласа по данным таблицы «Значения функции Лапласа Ф(х)», используя при необходимости линейное интерполирование. Считаем при x 0= –¥ и x 9= +¥. Теоретическую вероятность (столбец 5) находим по формуле pi=F(x i+1)-F(x i) и записываем результаты между строк столбца 4. Затем вычисляем  и выписываем
и выписываем  (количество попаданий в i-й интервал) из табл. 2 нашего примера (табл. 3).
(количество попаданий в i-й интервал) из табл. 2 нашего примера (табл. 3).
|
|
|
Таблица 3
Проверка гипотезы о нормальном распределении величины Х
| i | Границы интервалов | 
| 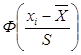
| pi | 
| 
|
| 72,99-73,46 73,46-73,93 73,93-74,40 74,40-74,87 74,87-75,34 75,34-75,81 75,81-76,28 76,28-76,75 76,75-77,22 | - -2,26 -1,58 -0,90 -0,23 0,45 1,12 1,79 2,47 + | -0,5000 -0,4881 -0,4429 -0,3159 -0,0910 0,1736 0,3686 0.4633 0,4931 0,5000 | 0,0119 0,0452 0,1270 0,2249 0,2646 0,1950 0,0947 0,0298 0,0069 | 1,1067 4,2036 11,8110 20,9157 24,6078 18,1350 8,8071 2,7714 0,6417 |
Исходя из наших данных для x 1 отношение  -2,26. Таким образом, в соответствии с таблицей «Значения функции Лапласа Ф(х)», значение:
-2,26. Таким образом, в соответствии с таблицей «Значения функции Лапласа Ф(х)», значение:
y = 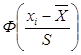 =-0,4881. Если отношение
=-0,4881. Если отношение 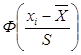 не имеет конкретного значения в таблице, а находится в интервале между приведенными в таблице значениями, тогда используем метод линейной интерполяции.
не имеет конкретного значения в таблице, а находится в интервале между приведенными в таблице значениями, тогда используем метод линейной интерполяции.
Для расчета значения 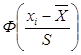 требуется провести линейную интерполяцию с использованием данных таблицы «Значения функции Лапласа Ф(х)»,. Например пусть некоторая функция y=y(x) представляет из себя таблицу, где хi– значение аргумента, yi – соответствующее значение функции. Требуется найти значение функции для аргумента х1<x<x2 по данным значения y1<y<y2 или наоборот по данному у найти х. Предположим, что на участке (х1, х2) график функции имеет линейную зависимость, тогда уравнение прямой будет иметь вид
требуется провести линейную интерполяцию с использованием данных таблицы «Значения функции Лапласа Ф(х)»,. Например пусть некоторая функция y=y(x) представляет из себя таблицу, где хi– значение аргумента, yi – соответствующее значение функции. Требуется найти значение функции для аргумента х1<x<x2 по данным значения y1<y<y2 или наоборот по данному у найти х. Предположим, что на участке (х1, х2) график функции имеет линейную зависимость, тогда уравнение прямой будет иметь вид  . Поскольку отрезок [x1,x2] мал, то в точке х ордината у(х) мало отличается от ординаты прямой. Из уравнения прямой находим неизвестное х или у.
. Поскольку отрезок [x1,x2] мал, то в точке х ордината у(х) мало отличается от ординаты прямой. Из уравнения прямой находим неизвестное х или у.
Дальше рассчитываем р i=0,5000-0,4881=0,01195. По формуле  определяем
определяем  =93·0,4922=0,7254.Аналогично проводим расчеты по всем данным, заполняем таблицу 3. Примечание. Первое значение
=93·0,4922=0,7254.Аналогично проводим расчеты по всем данным, заполняем таблицу 3. Примечание. Первое значение 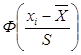 в таблице записываем (– 0,5000), а последнее (+0,5000).
в таблице записываем (– 0,5000), а последнее (+0,5000).
Для расчета критерия Пирсона  объединим первые и последние два интервала (читай теорию). Используя данные табл.3, рассчитаем критерий согласия Пирсона
объединим первые и последние два интервала (читай теорию). Используя данные табл.3, рассчитаем критерий согласия Пирсона  . Число интервалов определяется с учетом того, что число попаданий (частота)
. Число интервалов определяется с учетом того, что число попаданий (частота) 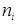 в один интервал не должно быть меньше 5, в ином случае его нужно объединить с соседним интервалом/ интервалами, таким образом, чтобы указанное условие было соблюдено. В нашем случае число интервалов К =8. Для расчета числа степеней свободы необходимо знать число параметров рассматриваемого закона распределения r. Для нормального закона распределения мы имеем два параметра – математическое ожидание (среднее арифметическое выборки) и дисперсию вариационного ряда (стандартное отклонение). Таким образом, число параметров, для которых были найдены оценки, r =2. Число степеней свободы f = К – r –1=8–2–1=5. Так как
в один интервал не должно быть меньше 5, в ином случае его нужно объединить с соседним интервалом/ интервалами, таким образом, чтобы указанное условие было соблюдено. В нашем случае число интервалов К =8. Для расчета числа степеней свободы необходимо знать число параметров рассматриваемого закона распределения r. Для нормального закона распределения мы имеем два параметра – математическое ожидание (среднее арифметическое выборки) и дисперсию вариационного ряда (стандартное отклонение). Таким образом, число параметров, для которых были найдены оценки, r =2. Число степеней свободы f = К – r –1=8–2–1=5. Так как  есть мера суммарного отклонения между моделью (теоретическим распределением) и экспериментальным распределением, сравним рассчитанное значение
есть мера суммарного отклонения между моделью (теоретическим распределением) и экспериментальным распределением, сравним рассчитанное значение  с теоретическим (табличным). Используя данные таблицы «Квантили
с теоретическим (табличным). Используя данные таблицы «Квантили  , удовлетворяющие условию
, удовлетворяющие условию  », находим, что рассчитанное значение
», находим, что рассчитанное значение  находится в интервале15,1<
находится в интервале15,1<  =16,38<16,7. По этой же таблице определяем вероятность согласования выдвинутой нами гипотезы о нормальном распределении с истинным распределением. Значению
=16,38<16,7. По этой же таблице определяем вероятность согласования выдвинутой нами гипотезы о нормальном распределении с истинным распределением. Значению  =15,1 соответствует q=0.99, а значению
=15,1 соответствует q=0.99, а значению  =16,7 соответствует q=0.995. Следовательно, гипотеза о нормальном распределении не согласуется с истинным распределением с вероятностью 99–99,5%.
=16,7 соответствует q=0.995. Следовательно, гипотеза о нормальном распределении не согласуется с истинным распределением с вероятностью 99–99,5%.
|
|
|
На полученной гистограмме относительных частот (рис.2 нашего примера) максимум находиться на середине интервала [72,99;77,22], поэтому рассмотрим предположение о наличии логарифмически нормального распределения.
Выдвинем и проверим гипотезу о логарифмическом нормальном распределении. Оценим параметры этого распределения по формулам. Находим, что:
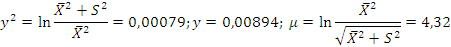
Тогда предполагаемая функция плотности вероятностей имеет вид:
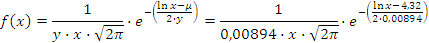

Сделаем проверку гипотезы о логарифмически нормальном распределении по критерию согласия Пирсона по таблице «Квантили  , удовлетворяющие условию (табл. 4):
, удовлетворяющие условию (табл. 4):
 »:
»:
Таблица 4
|
|
|


