 |
Структурные средние вариационного ряда.
|
|
|
|
Во многих случаях сгруппированные ранее данные необходимо разгруппировать для более полного анализа (так поступают, например, с вторичными данными).
Для более полного анализа используют так называемые структурные средние: моду, медиану, квартиль, децили, процентили.
1) Мода – наиболее часто встречающийся вариант, типичное значение.
В дискретном ряду мода – это вариант с наибольшей частотой
| Размер обуви | Количество купленных пар |
| Итого |
В интервальном ряду мода рассчитывается по формуле
s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 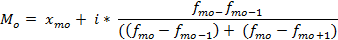
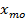 – нижняя граница модального интервала.
– нижняя граница модального интервала.
 – размер модального интервала
– размер модального интервала
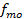 ,
, 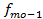 ,
, 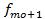 - частота модального интервала, интервала – перед модальной, интервала – после модального.
- частота модального интервала, интервала – перед модальной, интервала – после модального.
Модальный интервал – это интервал с наибольшей частотой.
Например:
| Рост, см. | Кол-во, чел. | Накопленная высота |
| 160 – 166,5 166,5 – 173 173 – 179,5 179,5 – 186 Итого |
Модальный интервал 166,5 – 173
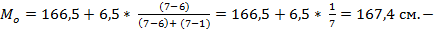 наиболее часто указанный
наиболее часто указанный
рост
2) Медиана – делит вариационный ряд пополам, причем в одной половине значения меньше медианы – в другой больше.
Медиана там, где накопленная частота, впервые составляет половину или больше половины суммы частот ряда (это медианный интервал).
Медиана определяется по формуле
 =
= 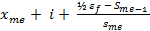
Xme – нижняя граница медианного интервала.
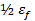 – полусумма частот ряда
– полусумма частот ряда
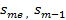 – накопленная частота медианного интервала, интервала передмедианного.
– накопленная частота медианного интервала, интервала передмедианного.
Накопленная частота – сумма частот друг за другом по цепочке – нарастающим шагом.
Медианный интервал: 166,5 – 173
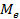 =
= 
Это значит, что у половины опрошенных рост меньше, чем 167,75 см., у половины больше.
3) В квартиле – отсекают четвертые части ряда:
|
|
|
3.1 Первый (нижний) квартиль отсекают ¼
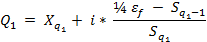
Первый квартильный интервал 160 – 166,5
Q1 = 160 + 6,5 
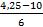 = 164,6 см.
= 164,6 см.
Это значит, что у 4-х человек рост меньше, чем 164,6 см., а у 13 больше.
3.2 Второй квартильный интервал отсекает 2 четверти ряда, то есть соответствует медиане.
3.3 Третий (верхний) квартиль отсекает ¾ ряда.
Q1 = XQ1 +  *
* 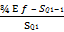
Третий квартиль 166,5 – 173
Q1 = 166,5 + 6,5  6,5 +
6,5 + 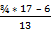 = 170 см. У 13 человек рост ниже 170 см., а у 4-х выше.
= 170 см. У 13 человек рост ниже 170 см., а у 4-х выше.
4) Децили – отсекают десятые части ряда (их 9) – формула аналогичная.
5) Процентили – отсекают сотые части ряда (их 99)
Показатели корреляции.
На определенном этапе маркетинговых исследований возникает необходимость в определении взаимосвязей между признаками. Например: взаимосвязь уровня дохода от типа населенного пункта, количество потребления кондитерских изделий от пола или возраста и т.п.
При этом признаки могут быть количественные (выраженные в цифрах) – возраст, доход и т.п. и качественные, которые измерению не поддаются – социальное положение, место проживания и т.п.
Анализ взаимосвязей между признаками показывает кориоционным анализом.
При этом используют следующие коэффициенты:
1. Коэффициент ассоциации – для определения взаимосвязи между двумя качественными признаками, каждый из которых состоит из 2-х групп, выделенных по альтернативе (да/ нет, м/ж и т.д.).
Этот коэффициент определяется по формуле:
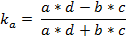
Для расчета используются следующие макеты:



Например:
- имеются данные о распределении работников фирмы по полу и оценки содержания работы
| Считают работу | мужчины | Женщины | всего |
| интересной неинтересной | 300  130
130 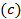
| 201 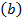
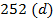
| 501  381
381 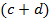
|
| Итого | 430 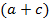
| 453 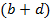
| 883 (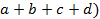
|
 =
= 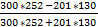 =
= 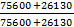 =
= 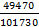 = 0, 486
= 0, 486
Связь считается подтвержденной больше или равной:
 = |0,5|
= |0,5|
В нашем случае отношение к работе почти не зависит от пола.
|
|
|
2) Коэффициент контингенции – имеет ту же область применения, что и  , но считается более точной.
, но считается более точной.
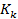 =
= 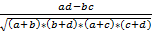
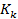 =
=  =
=  <
< 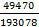 = 0, 26
= 0, 26
Связь подтверждается, если 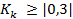
В нашем случае этот коэффициент показывает еще более слабую зависимость.
3). Коэффициент Пирсона и Чупрова – используют при изучении зависимости между двумя качественными признаками (если они имеют больше чем 2 группы) или между качественным и количественным признаком.
Коэффициент Пирсона
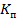 =
= 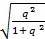
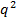 - показатель взаимной сопряженности.
- показатель взаимной сопряженности.
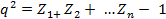
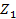 = (
= (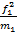 +
+ 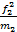 +
+  ):
): 
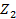 = ((
= ((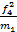 +
+ 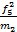 +
+ 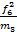 ):
):  и т.д.
и т.д.
Например:
Необходимо определить зависимость между себестоимостью и суммой расходов на управление.
| Накладные расходы | Себестоимость | Итого | ||
| Низкая | средняя | высокая | ||
| Низкие Средние Высокие Итого | 5 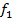 11
11 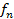 3
3  19
19 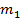
| 15 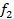 13
13 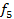 20
20 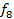 38
38 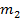
| 10 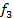 4
4 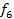 15
15 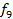 29
29 
| 20  28
28  38
38 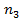
|
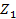 =(
=(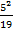 +
+ 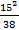 +
+ 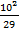 ): 20 = 0,53
): 20 = 0,53
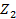 =(
=( +
+  +
+  ): 28 = 0,41
): 28 = 0,41
 =(
=(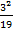 +
+ 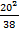 +
+  ): 38 = 0,49
): 38 = 0,49
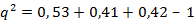 = 0, 38
= 0, 38
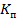 = r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
= r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  = 0,51
= 0,51
Связь подтверждается если  |0,5|
|0,5|
Вывод: уровень себестоимости незначительно зависит от накладных расходов.
Коэффициент Чупрова:
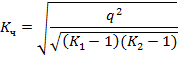
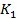 и
и 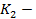 количество групп по первому и второму признакам.
количество групп по первому и второму признакам.
 = 0,42
= 0,42
Связь подтверждается если  ≥ |0,3|
≥ |0,3|
Поскольку этот коэффициент считается более точным чем коэффициент Пирсона, то можно сказать, что связь между размером себестоимости и накладными расходами существует.
4) Коэффициент корреляции рангов (Спирмина) – показывает взаимосвязь между количественными признаками.
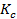 = 1-
= 1- 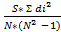
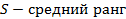
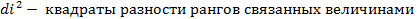 r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 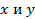

Например:
| № | Доход семьи, тыс. руб. (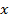 ) )
| Сумма расходов на питание (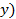
| Ранг | 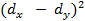
| |
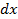
| 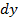
| ||||
| Итого | - | - | - |
Наименьшее значение получает ранг один и так далее по возрастанию.
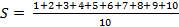 = 5,5
= 5,5
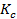 = 1-
= 1-  = 0,84
= 0,84
Связь подтверждается 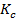 ≥ |0,5|
≥ |0,5|
|
|
|
В нашем примере прослеживается значительная зависимость между суммой расходов семьи на питание и уровнем дохода.
Практическая работа
Определение взаимосвязи между признаками
Задача № 1.
Определить зависимость между отношением к рекламе средств личной гигиены и уровен образования
| Высшее образование | Отношение к рекламе | Всего | |
| положительное | отрицательное | ||
| Есть Нет | |||
| Итого |
Задача №2.
Определить зависимость между семейным положением и назначением покупки телевизора
| Куда покупается телевизор | Семейное положение | Всего | ||
| Женат (замужем) | Не женат (не замужем) | Разведен (Разведена) | ||
| В гостиную В спальню На кухню На дачу | ||||
| Итого |
Задача № 3.
Определить зависимость между уровнем дохода и размером диагонали покупаемого телевизора
| Уровень дохода, тыс. руб. | Выбираемая диагональ | Всего | |||
| 54-66 | 72-81 | свыше 81 | |||
| До 5 5-10 10-15 15-25 Свыше 25 | |||||
| Итого |
Задача №4.
Определить зависимость между уровнем дохода на одного члена семьи и количеством человек в семье.
| № | Уровень дохода на 1 члена семьи, тыс. руб. (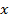 ) )
| Количество членов семьи, чел. (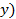
| Ранги | 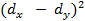
| |
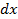
| 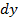
| ||||
| Итого | - | - | - |
 = 5
= 5
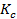 = 1-
= 1-  = 0,2
= 0,2
Связь подтверждается, так как 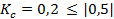
Вывод: зависимость между уровнем дохода на 1 члена семьи и количеством человек в семье не подтверждается.
Задача №3
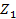 =(
=(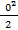 +
+ 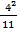 +
+ 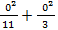 ): 4 = 0,36
): 4 = 0,36
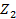 =(
=( +
+ 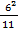 +s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>3</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t> </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
+s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>3</m:t></m:r></m:den></m:f><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t> </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 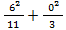 ): 13 = 0,54
): 13 = 0,54
 =(
=( +
+  +
+  ): 7 = 0,33
): 7 = 0,33
|
|
|
 =
= 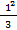 : 3 = 0,33
: 3 = 0,33
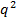 = 0,36 + 0, 54+0,33 + 0,33 – 1 = 0,56
= 0,36 + 0, 54+0,33 + 0,33 – 1 = 0,56
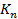 = r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
= r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 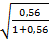 = 0,60
= 0,60
Связь подтверждается, так как 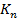 = 0,60 ≥ |0,5|
= 0,60 ≥ |0,5|
Вывод: выбираемая диагональ зависит от уровня дохода.
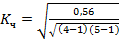 = 0,402
= 0,402  = 0,402
= 0,402
 ≥ |0,03|
≥ |0,03|
Вывод: связь подтверждается.
Задача № 2.
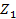 =(
=( +
+ 
 ): 12 = 0,47
): 12 = 0,47
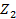 =(
=(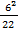 +
+  +
+  ): 10 = 0,408
): 10 = 0,408
 =(
=( +
+ 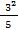 +
+  ): 8 = 0,347
): 8 = 0,347
 =
= 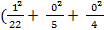 : 1 = 0,045
: 1 = 0,045
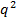 = 0,47 + 0, 408+0,347 + 0,045 – 1 = 0,27
= 0,47 + 0, 408+0,347 + 0,045 – 1 = 0,27
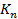 = r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
= r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 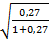 = 0,46
= 0,46
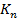 = 0,45 ≤ |0,5|
= 0,45 ≤ |0,5|
Вывод: назначение покупки телевизора почти не зависит от семейного положения, так как 0,44 ≤ |0,5| на 0,06.
Задача № 1.
 =
= 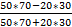 =
=  =
= 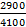 = 0,70
= 0,70
Вывод: есть зависимость между отношением к рекламе средств личной гигиены и уровнем образования.
 = 0,7
= 0,7  ≥|0,5|
≥|0,5|
6. Ошибка выборки. Определение оптимального объема выборки.
Поскольку выборочные исследования всегда предполагают ошибку, то при распространении полученных результатов на всю совокупность необходимо эту ошибку учитывать.
При расчете ошибки выборки необходимо знать, что исследования могли проводиться относительно количественного признака или относительно доли лиц в совокупности обладающих изучаемым признаком.
Сначала рассчитываем 1-ую ошибку
1. 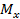 =
= 
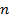 – количество единиц в выборке
– количество единиц в выборке
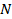 – количество единиц в совокупности
– количество единиц в совокупности
2. При изучении доли
Mw = 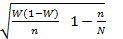
 – доля единиц в выборке обладающих изучаемым признаком.
– доля единиц в выборке обладающих изучаемым признаком.
 =
= 
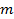 -количество единиц в выборке обладающих изучаемым признаком.
-количество единиц в выборке обладающих изучаемым признаком.
Средняя ошибка выборки гарантирует точность результата с вероятностью 68 %. По этому, рассчитываем предельную ошибку выборки
= 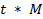
 – коэффициент доверия, который показывает, с какой вероятностью можно гарантировать точность результата.
– коэффициент доверия, который показывает, с какой вероятностью можно гарантировать точность результата.
| t | Вероятность |
| 1,0 1,5 2,0 2,5 4,0 | 0,6827 0,8864 0,9545 0,9876 0,999 |
| 0,997 |
Чаще всего принимают  = 2,0
= 2,0
Пример.
По ниже приведенным данным определить:
1) средний уровень дохода потенциальных покупателей;
2) дисперсию;
3) с вероятностью 95, 45% средний уровень дохода всех потенциальных покупателей;
4) с вероятностью 95,45 % долю покупателей во всей совокупности с доходом от 15-30 тыс. руб.
Дано: опрошено 100 потенциальных покупателей в магазине (10 % - ая выборка) и получены следующие результаты.
| Уровень дохода, тыс. руб. | Количество чел. 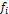
| Середина интервала 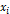
| 
| |  – – 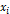 | |
| ( – – 
| ( – –  * * 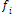
|
| До 15 15 – 20 20 – 30 Свыше 30 | 12, 5 17,5 | 612, 5 | 10, 125 5,125 2,375 12,375 | 102,52 26,27 5,641 153,141 | 1025,2 919,45 225,625 2297,11 | |
| Итого | - | 2262,5 | - | - | 4467,38 |
|
|
|
1) 
2) 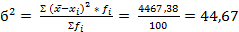
3) 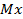 =
= 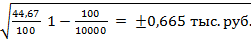
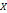 = 2 (± 0,665) ± 1,33 тыс. руб.
= 2 (± 0,665) ± 1,33 тыс. руб.
Вывод: уровень дохода у всех потенциальных потребителей в среднем составляет 22,65 ± 1,33, то есть находится в пределах 21,32-23,98 тыс. рублей.
4) 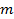 = 75 чел.
= 75 чел.
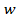 = 75/100 = 0, 75
= 75/100 = 0, 75
 =
= 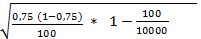 = ± 0,01 тыс. руб.
= ± 0,01 тыс. руб.
= 2  (±0,01) = 0,02 тыс. руб.
(±0,01) = 0,02 тыс. руб.
Вывод: доля покупателей с доходом от 15 до 30 тыс. руб. во всей совокупности составляет 0,75 ± 0,02, то есть в пределах 0,73 – 0,77 (73 – 75%).
В некоторых случаях приходится иметь дело с так называемой малой выборкой (1%). В этом случае значение выражения
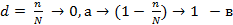 этом случае формулы средней ошибки упрощаются и принимают вид
этом случае формулы средней ошибки упрощаются и принимают вид

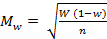
Например: выборочное исследование затрат времени студентов на подготовку к контрольной работе показало следующие результаты.
Затраты, чел: 8,5; 8; 7,8; 9; 7,2; 6,2; 8,4; 6,6.
Определить сколько в среднем студенту учебного заведения тратят времени на подготовку к контрольной работе (вероятность выбрать самостоятельно)
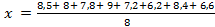 = 7,7 час.
= 7,7 час.
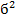 =
= 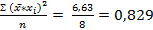
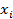
| 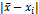
| (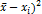
|
| 9,5 7,8 7,2 6,2 8,4 6,6 | 0,8 0,3 0,1 1,3 0,5 1,5 0,7 1,1 | 0,64 0,09 0,01 1,69 0,25 2,25 0,49 1,21 |
| Итого | 6,63 |
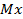 =
= 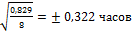
1 = 2  (± 0,322) = ± 0, 644 часов
(± 0,322) = ± 0, 644 часов
7,7 ±0,644 7,056 = 8,344
Вывод: студенты всего учебного заведения в среднем тратят на подготовку к контрольной работе 0,829 ± 0, 644 (час.), то есть от 0,354 до 1,473 час с вероятностью 95,45 %.
Для того, чтобы определить оптимальный объем выборки необходимо преобразовать формулы предельной ошибки выборки:
1. При изучении количественного признака


2. При исследовании доли

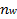 =
= 
Пример: определить сколько объектов из совокупности 507 промышленных предприятий надо проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в оплате налогов. По данным прошлого аналогичного исследования величина среднего квадратического отклонения составила 0,15, размер ошибки выборки предполагается получить не выше 0,15.
t = 3

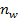 =
=  = 9 (предприятий)
= 9 (предприятий)
Среднее квадратическое отклонение при изучении доли определяется по формуле:
б = 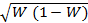
Практическая работа
Определить ошибки выборки и объем выборки
Задача № 1.
При контрольной проверке качество хлебобулочных изделий проведено 5% выборочного исследования партии батонов, при этом из 100 отобранных батонов 90 соответствовали требованиям стандартов. Средний вес одного батона в выборке составлял 500,5 гр. При среднем квадратическом отклонении ± 15,4 гр.
Определить средний вес батона во всей партии и долю батонов соответствующих требованию стандартов во всей партии. Вероятность выбрать самостоятельно.
Задача № 2.
При контрольной проверке качество поставленной в торговлю колбасы получены следующие данные о содержании поваренной соли в пробах (%): 4,6; 4.2;3,8; 4,3; 3,7; 3,9; 4,5; 4,4; 4,0; 3,9.
С вероятностью 0,95 определить средний % содержания соли во всей партии.
Задача № 3.
Исходя из требования ГОСТа необходимо установить оптимальный 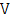 выборки из партии батонов (2000 шт.), чтобы с вероятностью 0,997 предельная ошибка не превысила 3% веса 500 гр. батона.
выборки из партии батонов (2000 шт.), чтобы с вероятностью 0,997 предельная ошибка не превысила 3% веса 500 гр. батона.
Решение.
1) Дано:
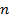 = 100 шт.
= 100 шт.
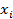 = 500,5 гр.
= 500,5 гр.
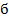 = ± 15,4 гр.
= ± 15,4 гр.
Найти:  ,
, 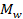 .
.
Решение:
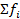 =
= 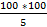 = 2000
= 2000
 =
= 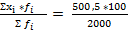 = 25, 025 гр.
= 25, 025 гр.
Mw = 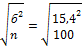 =
= 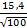 =
=  = ± 1,54 гр.
= ± 1,54 гр.
X = t 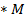
X = 2 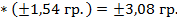
Вывод: 500,5 ± 3,08 гр.
от 497,42 до 503,58 гр.
Mw =  )=
)= 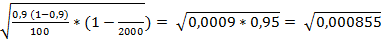 = ±0,03
= ±0,03

= 2 
Вывод: доля батонов соответствующих требованиям стандарта во всей партии составляет 0,9 ± 0,06, то есть в пределах 0,84 ± 0,96 (84-96%).
Задача 2
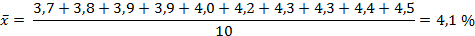
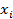
| | 
| 
|
| 3,4 3,8 3,9 3,9 4,0 4,2 4,3 4,3 4,4 4,5 | 0,4 0,3 0,2 0,2 0,1 0,1 0,2 0,2 0,3 0,4 | 0,16 0,09 0,04 0,04 0,01 0,01 0,04 0,04 0,09 0,16 |
| Итого | - | 0,68 |

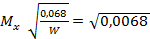 = ± 0,082 %
= ± 0,082 %
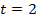
= 2 
Вывод: средний процент содержания соли во всей партии 4,1% ± 0,0164 %, то есть в пределах 4,0836 – 4,1164 %.
3). 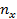 =
= 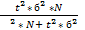
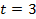
= 15 гр. 
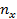 =
= 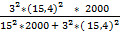 =
= 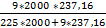 = 0, 039 гр. =
= 0, 039 гр. = 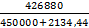 =
= 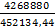 = 10 батонов
= 10 батонов
|
|
|


