 |
Резонансная длина волны вибратора
|
|
|
|
Резонансная длина волны вибратора
Рассматривая вибратор как двухпроводную симметричную разомкнутую линию длиной l, для входного сопротивления в предположении малых потерь имеем
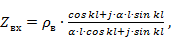
где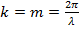 
- фазовая постоянная;
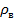- волновое сопротивление вибратора.
Так как вибратор эквивалентен неоднородной линии, то его волновое сопротивление зависит от длины. Одним из многих приближенных методов определения 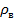является метод, основанный на определении волнового сопротивления из рассмотрения статической погонной емкости, приводящий к формуле
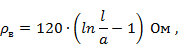
где l - длина плеча вибратора;
а - радиус его поперечного сечения.
При приближенных расчетах в случае тонких симметричных вибраторов можно считать, что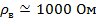 
.
Из формулы (5. 1) следует, что вибратор резонирует при 
или 
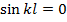; в обоих случаях входное сопротивление становится активным. Таким образом, вибратор находится в резонансе, когда длина его плеча кратна 
: 
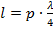, где р = 1, 2, 3 …, или когда полная длина вибратора кратна 
: 
. Длина волны λ вдоль вибратора мало отличается от длины волны в свободном пространстве, так как скорость распространения волн вдоль провода в случае малых потерь близка к скорости света.
В отличие от колебательного контура, вибратор обладает бесконечным дискретным набором резонансных волн. Наиболее длинная волна называется основной, остальные - гармониками. Основной волне соответствует значение р = 1, тогда λ = 4∙ l. Вибратор, длина которого определена с учетом последнего равенства, называется полуволновым. Опыт показывает, что в действительности длину вибратора для настройки в резонанс следует брать несколько короче. Это «укорочение вибратора» по сравнению с , соответствующее резонансу, невелико и тем больше, чем больше диаметр вибратора 2а. В среднем его можно принять равным 5%. Следовательно, если задана длина волны λ , то длина резонансного вибратора 
.
|
|
|
Это явление можно объяснить следующим образом. Под действием собственного поля излучения в вибраторе наводится э. д. с., добавочная по сравнению с э. д. с. линии. Если наведенную э. д. с. заменить падением напряжения на некотором сопротивлении, то это сопротивление оказывается индуктивного характера. Последнее вытекает из того, что это наведенное сопротивление компенсирует реактивное сопротивление антенны, когда длина плеча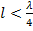 
, т. е. соответствующая длинная линия имеет емкостной характер сопротивления.
Распределение тока вдоль симметричного вибратора
Закон распределения тока вдоль симметричного вибратора вытекает из закона распределения тока вдоль двухпроводной разомкнутой линии.
Рассмотрим вибратор как идеальную двухпроводную развернутую линию, разомкнутую на конце. Амплитуда тока в исходной линии изменяется по закону
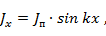
где 
- амплитуда тока в пучности стоячей волны;
х - координата, отсчитываемая от конца линии.
При одном и том же значении х токи в проводах равны по амплитуде и противоположны по направлению (рис. 5. 2, а). После развертывания проводов токи в обоих плечах полученного вибратора будут направлены в одну сторону (рис. 5. 2, б) и равны 
; 
.
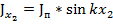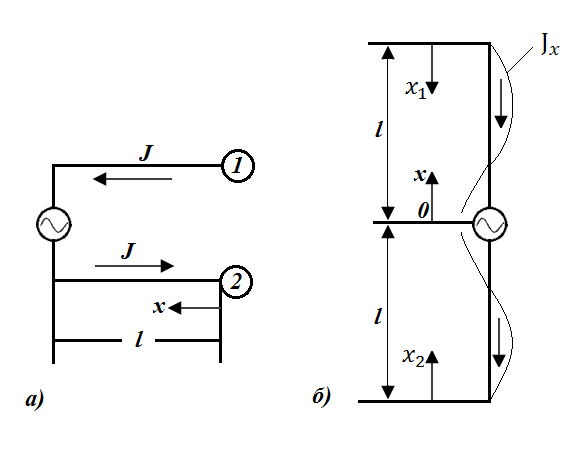
Рис. 5. 2. К выбору начала отсчета:
а - в исходной двухпроводной линии;
б - в симметричном вибраторе
Здесь координаты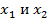 
отсчитываются в каждом проводе от внешнего конца.
Сместим начало координат в середину вибратора. Тогда, считая, что расстояние между проводами в месте подключения генератора ничтожно мало, можем записать
|
|
|
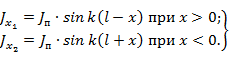
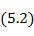
Таким образом, токи симметричных относительно центра точек вибратора одинаковы по амплитуде и фазе: J(x) = J(-x).
Входящий в формулы (5. 2) ток в пучности стоячей волны связан с током на входе вибратора 
соотношением 
.
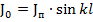Распределение зарядов вдоль вибратора легко установить, воспользовавшись известным из электродинамики законом сохранения заряда. Так как ток в вибраторе имеет только продольную составляющую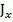 
, этот закон может быть записан в виде
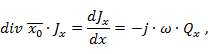
где Qx - погонная плотность заряда.
Отсюда
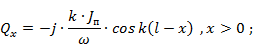
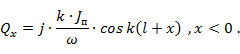
Полученный закон распределения заряда вдоль симметричного вибратора совпадает с законом распределения потенциала (напряжения) в разомкнутой на конце линии без потерь.
Распределение амплитуд тока и заряда вдоль вибраторов различной длины показано на рис. 5. 3.
Из рисунка видим, что в случае длины вибраторов, кратной нечетному числу полуволн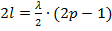 
, где р = 1, 2, 3…, ток распределен по косинусоидальному закону
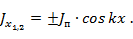
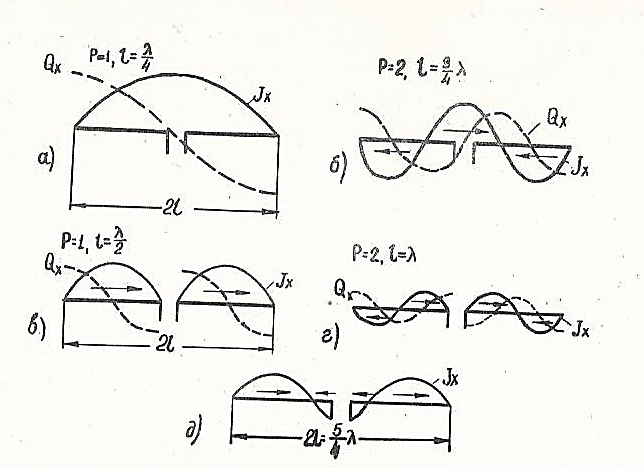
Рис. 5. 3. Распределение амплитуд тока и заряда:
а, б – по вибратору, длина которого кратна нечетному числу полуволн; в, г – по вибратору, длина которого кратна четному числу полуволн; д – при произвольной длине вибратора
В середине вибратора получается пучность тока, а заряд равен нулю (рис. 5. 3, а, б).
Если же длина вибратора кратна четному числу полуволн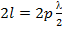 
, то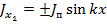 
; 
.
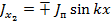Таким образом, в середине вибратора устанавливаются узел тока и пучность напряжения (заряда) (рис. 5. 3, в, г). При длине вибратора, не кратной 
, амплитуда тока на входных клеммах вибратора лежит в пределах от нуля до значения тока в пучности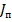 
в зависимости от длины вибратора (рис. 5. 3, д). Построение кривой распределения тока 
в этом случае следует производить, как и в разомкнутой линии, т. е. с концов вибратора, где всегда имеют место узел тока и пучность заряда.
До сих пор мы рассматривали симметричный вибратор, ток которого на концах равнялся нулю. Однако распределение амплитуд тока по вибратору можно изменить путем подсоединения к его концам металлических дисков или шаров, играющих роль сосредоточенных емкостей (такие вибраторы называют нагруженными). Вследствие заряда емкостей ток на концах вибратора отличен от нуля и кривая распределения его принимает вид, показанный на рис. 5. 4, а.
|
|
|
Рис. 5. 4. К изменению распределения тока по вибратору: а – путем подсоединения к его концам дисков или шаров; б – путем включения отрезков длинных линий в его плечи
Нагруженный вибратор эквивалентен ненагруженному большей длины
. Эквивалентное удлинение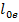 
зависит от величины емкости на конце, т. е. от формы и размеров присоединенного металлического тела. Для нагруженного вибратора, как и для ненагруженного, применима теория длинных линий.
Для регулировки в широких пределах распределения тока вдоль вибратора можно использовать включение в его плечи конденсаторов, катушек индуктивности или отрезков длинных линий (рис. 5. 4, б). Такая регулировка может понадобиться для получения тока одного направления в плечах вибратора сравнительно большой длины (несколько l).
|
|
|
