 |
§ 5. 6. Основные результаты строгой теории симметричного вибратора
|
|
|
|
Существуют два метода строгого решения задачи об излучении симметричного вибратора: метод интегро-дифференциального уравнения и метод собственных функций. Остановимся кратко на первом.
Рассмотрим симметричный вибратор (рис. 5. 12), плечи которого выполнены из очень тонкого полого цилиндрического провода ( 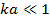 ) с бесконечно тонкими стенками. Между плечами вибратора включен источник э. д. с., создающий в кольцевом зазоре шириной
) с бесконечно тонкими стенками. Между плечами вибратора включен источник э. д. с., создающий в кольцевом зазоре шириной 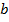 напряженность стороннего электрического поля
напряженность стороннего электрического поля 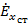 (рис. 5. 12, а).
(рис. 5. 12, а).

Рис. 5. 12. К расчету характеристик симметричного вибратора строгим методом: а - вид вибратора с источником э. д. с.; б - сторонний кольцевой магнитный ток в зазоре между плечами вибратора
Так как напряженность электрического поля в зазоре (щели) связана с плотностью поверхностного магнитного тока соотношением 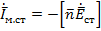 , можно считать, что вибратор возбуждается сторонним кольцевым магнитным током (рис. 5. 12, б), создающим в окружающем пространстве электромагнитное поле.
, можно считать, что вибратор возбуждается сторонним кольцевым магнитным током (рис. 5. 12, б), создающим в окружающем пространстве электромагнитное поле.
Под действием сторонней э. д. с. 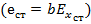 на поверхности вибратора возникает электрический ток, имеющий только одну составляющую
на поверхности вибратора возникает электрический ток, имеющий только одну составляющую 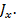 Этот ток является вторичным по отношению к стороннему магнитному току и создает в окружающем пространстве свое вторичное электромагнитное поле.
Этот ток является вторичным по отношению к стороннему магнитному току и создает в окружающем пространстве свое вторичное электромагнитное поле.
Так как по условию задачи радиус вибратора мал по сравнению с длиной волны и длиной вибратора, то излучением магнитного тока можно пренебречь и считать, что поле в произвольной точке пространства создается только электрическим током.
Ток 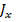 должен быть распределен так, чтобы поле на идеально проводящей поверхности вибратора удовлетворяло граничным условиям, которые для касательной составляющей электрического поля сводятся к выполнению равенства
должен быть распределен так, чтобы поле на идеально проводящей поверхности вибратора удовлетворяло граничным условиям, которые для касательной составляющей электрического поля сводятся к выполнению равенства 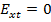 . Касательная составляющая электрического поля может быть найдена через векторные потенциалы магнитного
. Касательная составляющая электрического поля может быть найдена через векторные потенциалы магнитного 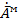 и электрического
и электрического 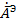 токов:
токов:
|
|
|
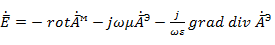
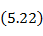
Так как в рассматриваемом случае имеется только одна составляющая векторного потенциала 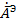 , а магнитный ток считается равным нулю, уравнение (5. 22) принимает вид
, а магнитный ток считается равным нулю, уравнение (5. 22) принимает вид
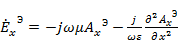

где
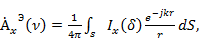
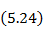
 составляющая векторного потенциала в точке наблюдения на поверхности вибратора;
составляющая векторного потенциала в точке наблюдения на поверхности вибратора; 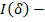 составляющая плотности поверхностного тока в точке
составляющая плотности поверхностного тока в точке 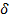 источника на поверхности проводника (рис. 5. 12, а);
источника на поверхности проводника (рис. 5. 12, а); 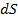 - элемент поверхности вибратора;
- элемент поверхности вибратора; 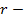 расстояние между точками наблюдения и источника.
расстояние между точками наблюдения и источника.
После подстановки выражения (5. 24) в (5. 23) и ряда преобразований получаем интегро-дифференциальное относительно тока вибратора 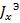 уравнение
уравнение
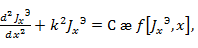
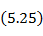
где 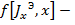 функция распределения тока по вибратору (функционал);
функция распределения тока по вибратору (функционал);
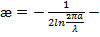 малый параметр (" параметр тонкости”);
малый параметр (" параметр тонкости”);
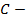 постоянный коэффициент.
постоянный коэффициент.
Если радиус вибратора устремить к нулю 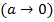 ., то малый параметр
., то малый параметр 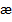 = 0 и уравнение (5. 25) принимает вид обычного дифференциального уравнения длинной линии без потерь
= 0 и уравнение (5. 25) принимает вид обычного дифференциального уравнения длинной линии без потерь
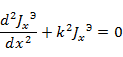
Решение этого уравнения 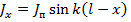 показывает, что ток распределен по синусоидальному закону только в вибраторе с исчезающе малым радиусом. Если отношение
показывает, что ток распределен по синусоидальному закону только в вибраторе с исчезающе малым радиусом. Если отношение 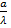 имеет малую, но конечную величину, решение уравнения (5. 25) может быть представлено в виде степенного ряда по степеням параметра
имеет малую, но конечную величину, решение уравнения (5. 25) может быть представлено в виде степенного ряда по степеням параметра 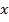 :
:
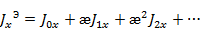
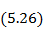
Если подставить данное решение в (5. 25), приравнять коэффициенты при одинаковых степенях 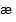 и использовать условие равенства нулю тока на концах вибратора, получим систему линейных дифференциальных уравнений, решение которых дает закон распределения тока по вибратору.
и использовать условие равенства нулю тока на концах вибратора, получим систему линейных дифференциальных уравнений, решение которых дает закон распределения тока по вибратору.
|
|
|
В связи с большими математическими трудностями при расчетах обычно ограничиваются первым приближением, т. е. в решении (5. 26) учитывают только первые два члена ряда. Это позволяет применять данный метод только к тонким антеннам  .
.
Известно строгое решение задачи и об излучении вибраторов большой толщины 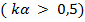 . Особенностью его является то, что для получения интегро-дифференциального уравнения используют граничные условия на поверхности вибратора для векторов магнитного поля.
. Особенностью его является то, что для получения интегро-дифференциального уравнения используют граничные условия на поверхности вибратора для векторов магнитного поля.
Из рассмотрения результатов строгой теории симметричного вибратора можно сделать следующие основные выводы:
1. Если длина сравнительно тонких вибраторов 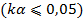 кратна или близка к целому числу полуволн, то распределение тока по вибратору в первом приближении не зависит от внешнего поля и является синусоидальным.
кратна или близка к целому числу полуволн, то распределение тока по вибратору в первом приближении не зависит от внешнего поля и является синусоидальным.
2. При длине вибратора, значительно отличающейся от резонансной (т. е. от  ), или в случае вибраторов средней
), или в случае вибраторов средней 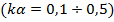 . и большой
. и большой 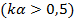 толщины распределение тока существенно отличается от синусоидального.
толщины распределение тока существенно отличается от синусоидального.
3. Зависимость распределения тока от толщины вибратора влияет на его диаграмму направленности: с увеличением толщины вибратора направления нулевого излучения заменяются направлениями минимального излучения, уровень которого тем выше, чем толще вибратор.
4. При питании вибратора в пучности тока сосредоточенной э. д. с. действительная часть входного сопротивления равна сопротивлению излучения и в первом приближении не зависит от формы и толщины вибратора. Величина активной составляющей входного сопротивления 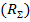 при этом такая же, как и в случае расчета по методу вектора Пойнтинга.
при этом такая же, как и в случае расчета по методу вектора Пойнтинга.
Реактивная составляющая заметно зависит от размеров поперечного сечения вибратора и его точной длины. В табл. 5. 1. приведены значения входного сопротивления цилиндрического полуволнового вибратора при различных значениях его радиуса. Так, при бесконечно тонких проводниках вибратора 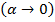 входное сопротивление вибратора длиной
входное сопротивление вибратора длиной 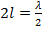 оказывается комплексным и равным
оказывается комплексным и равным

Таблица 5. 1
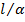
| 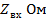
|
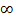
| 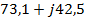
|
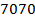
| 
|
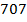
| 
|
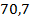
| 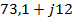
|
5. Резонансная длина вибратора меньше длины, точно кратной  , и тем меньше, чем толще вибратор.
, и тем меньше, чем толще вибратор.
|
|
|
Укорочение 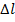 , необходимое для настройки в резонанс широко используемого на практике полуволнового вибратора, можно определить по формуле
, необходимое для настройки в резонанс широко используемого на практике полуволнового вибратора, можно определить по формуле 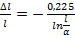
В случае тонких вибраторов укорочение составляет примерно 3 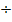 5% от длины
5% от длины 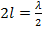 ; для толстых вибраторов -
; для толстых вибраторов - 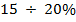 .
.
|
|
|


