 |
§5. 5. Действующая высота и входное сопротивление симметричного вибратора
|
|
|
|
Действующей высотой (или длиной) антенны называется высота (или длина) некоторой воображаемой антенны, которая при равномерном распределении тока по ее длине, равном току на входе реальной антенны (рис. 5. 8), и прочих равных условиях, создает поле, равное полю реальной антенны в направлении максимального излучения.
Для амплитуды электрического поля симметричного вибратора нами ранее была получена формула
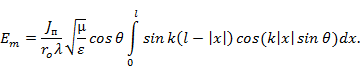
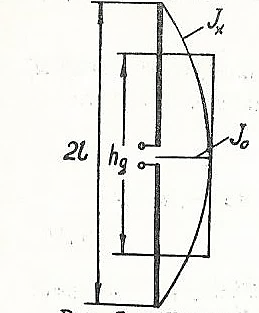
Рис. 5. 8. К расчету действующей высоты симметричного вибратора
Подставим в нее вместо тока в пучности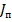 
ток на входных клеммах антенны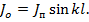 
Тогда
Сопоставляя (5. 15) с формулой для поля диполя в дальней зоне
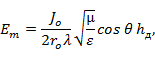
получаем выражение для действующей высоты вибратора
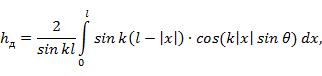
Вычисления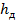 
по полученной формуле довольно громоздки, так как действующая высота, помимо размеров вибратора, является функцией рассматриваемого направления в пространстве θ . Однако в случае коротких вибраторов 
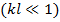или при рассмотрении поля только в экваториальной плоскости 
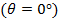выражение для 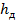заметно упрощается:
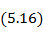
так как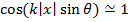 
при значениях аргумента 
.
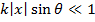Для установления физического смысла действующей высоты умножим числитель и знаменатель выражения (5. 16) на значение тока в пучности:
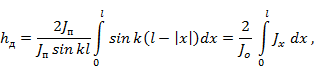
откуда
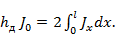
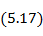
Таким образом, действующая высота определяется из равенства площадей эпюр тока на реальной антенне и эквивалентном диполе (рис. 5. 8). Формула (5. 17) при известном законе распределения тока позволяет легко рассчитать действующую высоту любого вибратора.
В случае вибраторов малой длины 
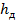формула (5. 16) упрощается и для получаем
|
|
|
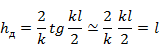
т. е. действующая высота вибратора равна половине его геометрической длины. В случае полуволнового вибратора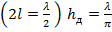 
При длине вибратора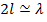 
формулой (5. 16) для расчета 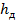пользоваться нельзя, так как такой расчет приводит к значению 
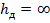. Это связано с использованием при выводе формулы (5. 16) приближенной теории, согласно которой ток на входных клеммах вибратора длиной 
принимался равным нулю, хотя вследствие потерь на излучение и в проводниках вибратора ток на входе имеет конечное значение. Для указанных размеров вибратора следует определять действующую длину, отнесенную к току в пучности, или рассчитать 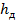по формулам, специально полученным с учетом реального закона распределения тока по вибратору.
Понятием действующей высоты удобно пользоваться при расчете антенн длинных и средних волн, а также при определении э. д. с. на входных клеммах приемных антенн.
Входное сопротивление симметричного вибратора определяется через напряжение и ток на его входе. Так как закон распределения тока и заряда (напряжения) вдоль вибратора мы считаем известным из теории длинных линий с потерями, то ту же самую теорию можно использовать и для определения входного сопротивления:
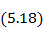
где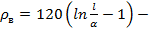 
волновое сопротивление вибратора;
фазовая постоянная;
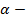постоянная затухания;
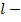длина эквивалентной линии с малыми потерями, равная длине одного плеча вибратора.
Освобождаясь в формуле (5. 18) от мнимости в знаменателе и пренебрегая величинами второго порядка малости, получаем
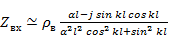
В выражении (5. 19) известны все величины, кроме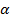 
, т. е. затухания в вибраторе, которое обусловлено потерями на излучение 
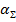(полезные потери) и омическими потерями 
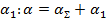. Так как обычно 
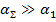, вследствие малых потерь в проводах вибратора, то 
.
|
|
|
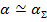В теории длинных линий доказывается, что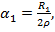 
где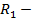 
погонное сопротивление проводников линии (вибратора). Запишем по аналогии
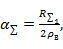(5. 20)
где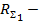 
сопротивление излучения, приходящееся на единицу длины вибратора (величина 
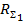предполагается распределенной равномерно вдоль вибратора).
Определим 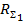. Мощность, излучаемая элементом 
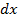вибратора, равна
где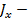 
амплитуда тока на элементе 
;
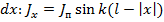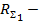сопротивление излучения элемента 
.
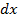Тогда мощность, излучаемая всем вибратором, может быть найдена как мощность, теряемая в эквивалентной двухпроводной линии длиной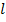 
с погонным сопротивлением потерь :
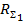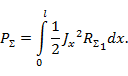
C другой стороны, мощность, излучаемая вибратором, равна
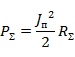
Приравнивая между собой последние две формулы и производя интегрирование, для 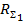получаем
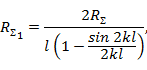
откуда
Таким образом, все величины, входящие в формулу (5. 19), известны, и, следовательно, входное сопротивление может быть определено для вибратора любой длины.
На рис. 5. 9 приведены зависимости активной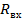 
и реактивной 
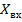составляющих входного сопротивления симметричного вибратора от отношения половины длины вибратора к длине волны для трех значений волнового сопротивления вибратора 
.
Рассмотрение графиков показывает явную зависимость составляющих входного сопротивления от 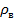или, что то же самое, от радиуса вибратора. Активная часть входного сопротивления имеет максимальное значение при длине вибратора 
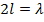. Максимум реактивной составляющей по сравнению с активной примерно вдвое меньше.
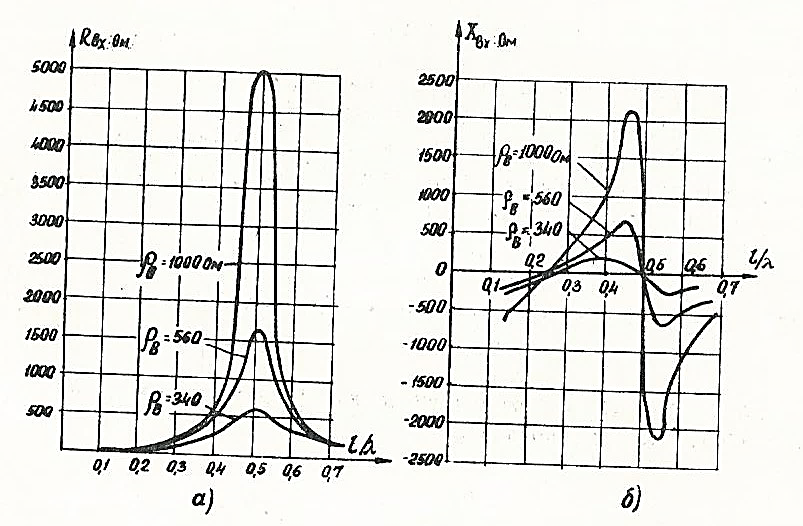
Рис. 5. 9. Входное сопротивление симметричного вибратора: а - активная составляющая; б - реактивная составляющая
В ряде случаев формулу (5. 19) для расчета входного сопротивления можно упростить. Так, если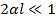 
, что имеет место или при сравнительно коротких вибраторах ввиду малого сопротивления излучения, или при тонких вибраторах, когда велико их волновое сопротивление (5. 20), выражение (5. 19) можно привести к виду
|
|
|
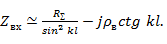
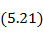
Приближенную формулу (5. 21), полученную для коротких или тонких вибраторов, можно использовать для расчета вибраторов длиной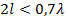 
. При больших длинах входное сопротивление вычисляют по общей формуле (5. 19).
В частном случае полуволнового и волнового вибраторов вычисления по формуле (5. 19) приводят к следующим значениям входного сопротивления:
Таким образом, при питании вибратора в пучности тока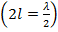 
его входное сопротивление значительно меньше, чем при питании в узле 
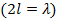. Кроме того, следует подчеркнуть совпадение значений входного сопротивления и сопротивления излучения полуволнового вибратора, что связано с совпадением при этой длине вибратора значений входного тока 
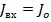и тока в пучности .
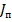Входное сопротивление вибратора вблизи резонанса (см. формулы (5. 19) и (5. 21)) зависит от частоты тем значительнее, чем выше его волновое сопротивление. Поэтому для расширения полосы пропускания следует применять вибраторы с пониженным волновым сопротивлением, т. е. вибраторы большой толщины. При этом графики зависимостей реактивного входного сопротивления вблизи резонансов сглаживаются (рис. 5. 9, б), а активная составляющая входного сопротивления вибратор длиной резко понижается (рис. 5. 9, а), что упрощает согласование с фидером.
На рис. 5. 10 показано несколько вариантов конструктивного выполнения широкополосных вибраторов. При этом провод вибратора не обязательно должен быть круглым и сплошным; он может быть выполнен из полой трубы большого диаметра (рис. 5. 10, а), плоской ленты, решетчатой или сплошной (рис. 5. 10, в, г), или состоять из нескольких параллельных проводов (рис. 5. 10, д).
Примеры широкополосных вибраторов в печатном исполнении приведены на рис. 5. 11.
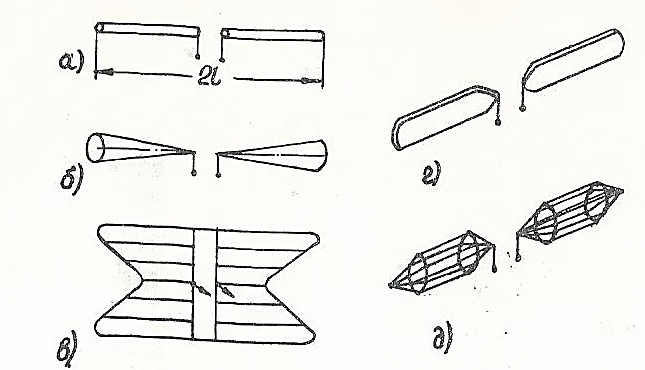
Рис. 5. 10. Конструкции широкополосных симметричных вибраторов: а - трубчатый; б - конический; в - плоскостной X-образный; г - плоский; д- вибраторт Надененко
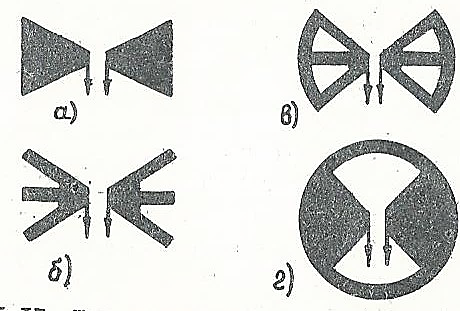
Рис. 5. 11. Широкополосные плоскостные вибраторы: а - треугольный; б – трехстержневой; в - треугольный с вырезами в плечах; г - вибратор " бабочка”
|
|
|
