 |
§ 5. 4. Сопротивление излучения симметричного вибратора
|
|
|
|
Полученные нами результаты позволяют перейти к рассмотрению вопроса о величине мощности, излучаемой вибратором при заданных распределении и амплитуде тока. От мощности нетрудно перейти к сопротивлению излучения, которое вводится как коэффициент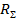 
, связывающий мощность излучения и ток в вибраторе. Так как обычно в антеннах распределение тока неравномерное, то сопротивление излучения будет зависеть от того, к току в каком сечении антенны оно отнесено. При синусоидальном распределении тока в антенне сопротивление излучения обычно определяют через ток в пучности Jп.
Излучаемая антенной мощность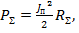 
откуда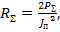 
где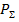 
- средняя во времени мощность излучения;
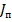- амплитуда тока в пучности;
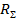- сопротивление излучения вибратора, отнесенное к квадрату тока в пучности.
Для определения 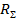воспользуемся методом вектора Пойнтинга.
Вообразим сферическую поверхность, находящуюся в свободном пространстве (рис. 5. 7, а), в центре которой расположен вибратор. Радиус сферы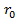 
выбираем достаточно большим, чтобы ее поверхность находилась в дальней зоне. Поток энергии за единицу времени через эту поверхность представляет собой излученную мощность. Аналитически эта мощность выражается следующим образом:
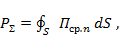
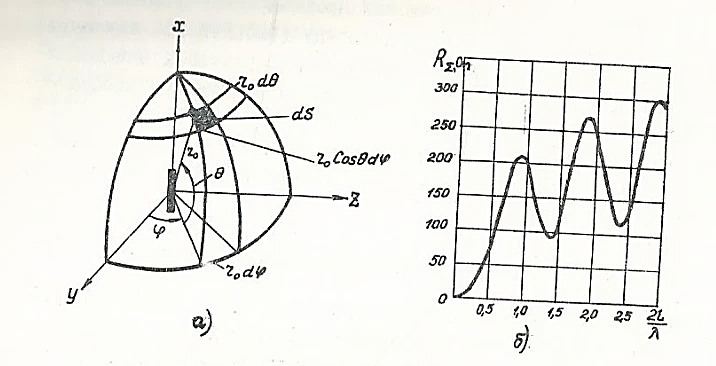
Рис. 5. 7. К определению сопротивления излучения вибратора:
а - отсчет углов; б - изменение сопротивления излучения вибратора от его относительной длины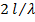 
где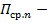 
среднее значение составляющей вектора Пойнтинга, нормальной к элементу dS;
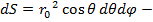элементарная площадка сферической поверхности, окружающей вибратор.
|
|
|
Подставляя в формулу (5. 9) вместо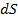 
его выражение, получаем
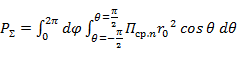
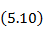
Энергия, проходящая по направлению r0 через элемент поверхности сферы, определяется составляющими векторов напряженности электрического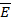 
и магнитного 
полей, перпендикулярных r0. Согласно теореме Пойнтинга 
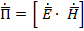. Для сферической волны, создаваемой вибратором на достаточно большом расстоянии, векторное произведение будет равно алгебраическому, так как 
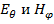взаимно перпендикулярны и между ними нет фазового сдвига 
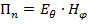, где 
мгновенные значения векторов напряженностей электрического и магнитного полей.
Переходя от мгновенных значений векторов поля к амплитудным, найдем среднее за период значение вектора Пойнтинга
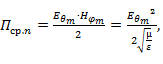
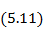
где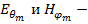 
амплитуды векторов напряженностей электрического и магнитного полей, причем их отношение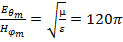 
Подставляя в уравнение (5. 10) среднее значение вектора Пойнтинга, определяемое формулой (5. 11), получаем
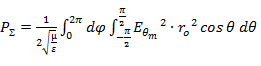
Формула (5. 12) имеет общий характер и может быть использована для расчета мощности излучения любой антенны.
Подставляя в (5. 12) вместо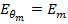 
его значение из выражения (5. 6), определенное ранее для симметричного вибратора, можем записать
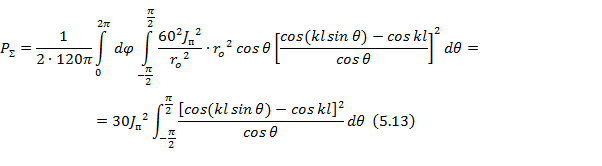
Интегрирование выражения (5. 13) приводит к следующей формуле
для сопротивления излучения вибратора, отнесенного к пучности тока
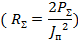
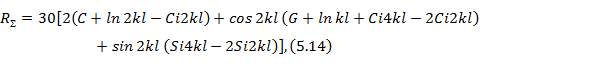
где С = 0, 577 - постоянная Эйлера;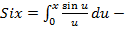 
интегральный синус; 
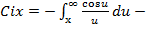интегральный косинус.
Из формулы (5. 14) следует, что сопротивление излучения симметричного вибратора зависит только от отношения 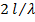. Результаты вычислений 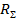по формуле (5. 14) в зависимости от 
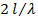приведены на рис. 5. 7, б.
Из рисунка видно, что с увеличением длины вибратора возрастает, пока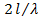 
. При дальнейшем увеличении 
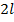до значения 
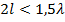сопротивление 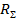уменьшается, так как появляются противофазные участки тока на вибраторе, что при том же токе в пучности приводит к уменьшению мощности и сопротивления излучения. Далее при увеличении отношения 
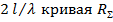приобретает колебательный характер с максимальными значениями при четном числе полуволн и минимальными - при нечетном.
|
|
|
Необходимо особо отметить два значения сопротивления излучения: 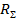= 73, 1 Ом - для вибратора длино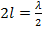й 
и 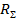= 200 Ом для вибратора длиной 
.
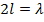Сопротивление излучения 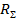было определено через ток в пучности 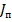. Его можно выразить также через ток в любом сечении, например через ток на входе антенны. В этом случае его можно рассчитать по формуле
|
|
|
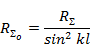
