 |
Первое начало термодинамики
|
|
|
|
Первое начало термодинамики представляет собой закон сохранения энергии, один из всеобщих законов природы (наряду с законами сохранения импульса, заряда и симметрии):
Энергия неуничтожаема и несотворяема; она может только переходить из одной формы в другую в эквивалентных соотношениях.
Первое начало термодинамики представляет собой постулат – оно не может быть доказано логическим путем или выведено из каких-либо более общих положений. Истинность этого постулата подтверждается тем, что ни одно из его следствий не находится в противоречии с опытом. Приведем еще некоторые формулировки первого начала термодинамики:
Полная энергия изолированной системы постоянна;
Невозможен вечный двигатель первого рода (двигатель, совершающий работу без затраты энергии).
Первое начало термодинамики устанавливает соотношение между теплотой Q, работой А и изменением внутренней энергии системы ΔU:
Изменение внутренней энергии системы равно количеству сообщенной системе теплоты минус количество работы, совершенной системой против внешних сил.
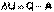 (I.1)
(I.1)
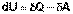 (I.2)
(I.2)
Уравнение (I.1) является математической записью 1-го начала термодинамики для конечного, уравнение (I.2) – для бесконечно малого изменения состояния системы.
Внутренняя энергия является функцией состояния; это означает, что изменение внутренней энергии ΔU не зависит от пути перехода системы из состояния 1 в состояние 2 и равно разности величин внутренней энергии U2 и U1 в этих состояниях:
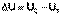 (I.3)
(I.3)
Следует отметить, что определить абсолютное значение внутренней энергии системы невозможно; термодинамику интересует лишь изменение внутренней энергии в ходе какого-либо процесса.
|
|
|
Рассмотрим приложение первого начала термодинамики для определения работы, совершаемой системой при различных термодинамических процессах (мы будем рассматривать простейший случай – работу расширения идеального газа).
Изохорный процесс (V = const; ΔV = 0).
Поскольку работа расширения равна произведению давления и изменения объема, для изохорного процесса получаем:
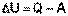 (I.1)
(I.1)
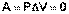 (I.4)
(I.4)
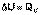 (I.5)
(I.5)
Изотермический процесс (Т = const).
Из уравнения состояния одного моля идеального газа получаем:
 (I.6)
(I.6)
Отсюда:
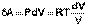 (I.7)
(I.7)
Проинтегрировав выражение (I.6) от V1 до V2, получим
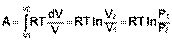 (I.8)
(I.8)
Изобарный процесс (Р = const).
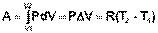 (I.9)
(I.9)
Подставляя полученные выражения для работы различных процессов в уравнение (I.1), для тепловых эффектов этих процессов получим:
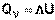 (I.10)
(I.10)
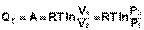 (I.11)
(I.11)
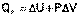 (I.12)
(I.12)
В уравнении (I.12) сгруппируем переменные с одинаковыми индексами. Получаем:
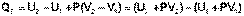 (I.13)
(I.13)
Введем новую функцию состояния системы – энтальпию H, тождественно равную сумме внутренней энергии и произведения давления на объем:

Тогда выражение (I.13) преобразуется к следующему виду:
 (I.14)
(I.14)
Т.о., тепловой эффект изобарного процесса равен изменению энтальпии системы.
Адиабатический процесс (Q = 0).
При адиабатическом процессе работа расширения совершается за счёт уменьшения внутренней энергии газа:
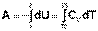 (I.15)
(I.15)
В случае если Cv не зависит от температуры (что справедливо для многих реальных газов), работа, произведённая газом при его адиабатическом расширении, прямо пропорциональна разности температур:
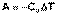 (I.16)
(I.16)
2. Закон Г.Гесса и следствия из него.
Как известно, большинство химических реакций сопровождаются выделением (экзотермические реакции) либо поглощением (эндотермические реакции) теплоты. Первое начало термодинамики дает возможность рассчитать тепловой эффект химической реакции при различных условиях её проведения.
Тепловой эффект (теплота) химической реакции – количество теплоты, выделившейся либо поглотившейся в ходе реакции. Тепловой эффект относят, как правило, к числу молей прореагировавшего исходного вещества, стехиометрический коэффициент перед которым максимален.
|
|
|
Например, реакцию окисления водорода в химической термодинамике записывают в виде:
Н2 + 1/2 О2 ––> Н2О
и тепловой эффект рассчитывают на 1 моль водорода.
Тепловые эффекты, сопровождающие протекание химических реакций, являются предметом одного из разделов химической термодинамики – термохимии. Определим некоторые понятия термохимии.
Теплота образования вещества – тепловой эффект реакции образования 1 моля сложного вещества из простых. Теплоты образования простых веществ принимаются равными нулю.
Теплота сгорания вещества – тепловой эффект реакции окисления 1 моля вещества в избытке кислорода до высших устойчивых оксидов.
Теплота растворения – тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Теплота растворения складывается из двух составляющих: теплоты разрушения кристаллической решетки (для твердого вещества) и теплоты сольватации:

Поскольку ΔНкр.реш всегда положительно (на разрушение кристаллической решетки необходимо затратить энергию), а ΔНсольв всегда отрицательно, знак ΔНраств определяется соотношением абсолютных величин ΔНкр.реш и ΔНсольв:
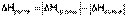
Основным законом термохимии является закон Гесса, являющийся частным случаем первого начала термодинамики:
Тепловой эффект химической реакции, проводимой в изобарно-изотермических или изохорно-изотермических условиях, зависит только от вида и состояния исходных веществ и продуктов реакции и не зависит от пути её протекания.
Выше было показано, что изменение энтальпии ΔН (тепловой эффект изобарного процесса Qp) и изменение внутренней энергии ΔU (тепловой эффект изохорного процесса Qv) не зависят от пути, по которому система переходит из начального состояния в конечное.
Рассмотрим некоторый обобщенный химический процесс превращения исходных веществ А1, А2, А3... в продукты реакции В1, В2, В3..., который может быть осуществлен различными путями в одну или несколько стадий:
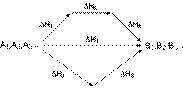
Согласно закону Гесса, тепловые эффекты всех этих реакций связаны следующим соотношением:
|
|
|
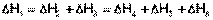 (I.17)
(I.17)
Практическое значение закона Гесса состоит в том, что он позволяет рассчитывать тепловые эффекты химических процессов. В термохимических расчетах обычно используют ряд следствий из закона Гесса:
1. Тепловой эффект прямой реакции равен по величине и противоположен по знаку тепловому эффекту обратной реакции (закон Лавуазье – Лапласа).
2. Для двух реакций, имеющих одинаковые исходные, но разные конечные состояния, разность тепловых эффектов представляет собой тепловой эффект перехода из одного конечного состояния в другое.
С + О2 ––> СО + 1/2 О2 ΔН1
С + О2 ––> СО2 ΔН2
СО + 1/2 О2 ––> СО2 ΔН3
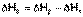 (I.18)
(I.18)
3. Для двух реакций, имеющих одинаковые конечные, но разные исходные состояния, разность тепловых эффектов представляет собой тепловой эффект перехода из одного исходного состояния в другое.
С(алмаз) + О2 ––> СО2 ΔН1
С(графит) + О2 ––> СО2 ΔН2
С(алмаз) ––> С(графит) ΔН3
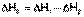 (I.19)
(I.19)
4. Тепловой эффект химической реакции равен разности сумм теплот образования продуктов реакции и исходных веществ, умноженных на стехиометрические коэффициенты.
 (I.20)
(I.20)
5. Тепловой эффект химической реакции равен разности сумм теплот сгорания исходных веществ и продуктов реакции, умноженных на стехиометрические коэффициенты.
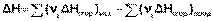 (I.21)
(I.21)
В качестве примера рассмотрим расчет теплового эффекта реакции окисления одного моля глюкозы (теплота образования кислорода по определению равна нулю):
С6Н12О6 + 6 О2 ––> 6 СО2 + 6 Н2О
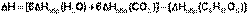
Величины тепловых эффектов химических реакций зависят от условий, в которых проводятся реакции. Поэтому табличные значения теплот различных процессов принято относить к стандартному состоянию – температуре 298 К и давлению 101325 Па (760 мм. рт. ст.; 1 атм.); величины тепловых эффектов при данных условиях называют стандартными тепловыми эффектами и обозначают ΔН°298 и ΔU°298 соответственно.
3. Уравнение Кирхгоффа и его анализ.
В общем случае тепловой эффект химической реакции зависит от температуры и давления, при которых проводится реакция. Влиянием давления на ΔН и ΔU реакции обычно пренебрегают. Влияние температуры на величины тепловых эффектов описывает закон Кирхгофа:
|
|
|
Температурный коэффициент теплового эффекта химической реакции равен изменению теплоемкости системы в ходе реакции.
Продифференцируем ΔН и ΔU по температуре при постоянных давлении и температуре соответственно:
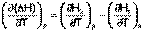 (I.22)
(I.22)
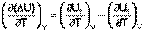 (I.23)
(I.23)
Производные энтальпии и внутренней энергии системы по температуре есть теплоемкости системы в изобарных и изохорных условиях Cp и Cv соответственно:
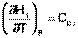 (I.24)
(I.24)
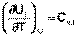 (I.25)
(I.25)
Подставив выражения (I.24, I.25) в (I.22, I.23), получаем математическую запись закона Кирхгофа:
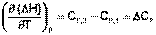 (I.26)
(I.26)
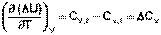 (I.27)
(I.27)
Для химического процесса изменение теплоемкости задается изменением состава системы и рассчитывается следующим образом:
 (I.28)
(I.28)
 (I.29)
(I.29)
Если проинтегрировать выражения (I.26, I.27) от Т = Т1 до Т = Т2, считая ΔСp (ΔСv) не зависящим от температуры, получим интегральную форму закона Кирхгофа:
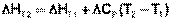 (I.30)
(I.30)
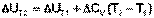 (I.31)
(I.31)
Поскольку обычно известны табличные значения стандартных тепловых эффектов ΔН°298 и ΔU°298, преобразуем выражения (I.30, I.31):
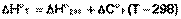 (I.32)
(I.32)
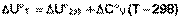 (I.33)
(I.33)
При расчете изменения теплового эффекта реакции в большом интервале температур необходимо учитывать зависимость теплоёмкости от температуры, которая выражается степенным рядом C°p = aT + bT2 + cT3; коэффициенты a, b, c приведены в справочниках.
Теплоемкость, уравнения Кирхгофа.
Теплоемкость - количество теплоты необходимое для нагрева единицы массы вещества на 10 К (удельная ед. массы, молярная 1 моля).
Истинная теплоемкость – отношение бесконечно малого количества теплоты, которое было подведено к телу к бесконечно малому изменению температуры, которое при этом наблюдалось. С = δQ/δT.
Средняя теплоемкость – отношение количества подведенной теплоты, к единицы массы вещества и к разности изменения температуры. С = Q/T 2 - T1.
Так как теплота, подведенная при постоянном V, или P соответственно равна приращению внутренней энергии и энтальпии то можно записать:
V = const, dQv = dU = nCvdT
P = const, dQp = dH = nCpdT. Если известна Cv, то можно получить Cp и наоборот.
Возьмем частную производную по Т от H = U + pV при P = const.
(δH/δT)p = (δU/δT)p +p (δV/Tδ)p
С другой стороны.
Cp - Cv =(δH/δT)p - (δU/Tδ)V = (δU/δT)p + p (δV/δT)p - (δU/Tδ)V.
Внутренняя энергия не зависит от давления и объема (δU/δT)p = (δU/Tδ)V = 0.
R = p (δV/Tδ)p – работа идеального газа против внешних сил при его нагреве на 10 К.
Иначе выражение получается при дифференцировании W = p∆V.
Теплоемкость зависит от температуры, эту зависимость для различных веществ находят опытным путем и помещают в справочники в виде интерполяционных уравнений.
|
|
|
Связь между истинной и средней теплоемкостями:
С = Q/(T 2 - T1).
Сp = δQ/δT, dQp = Cp*dT, 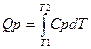
С = (1/(T 2 - T1))* 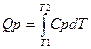 .
.
Зависимость теплового эффекта от Т.
(δ∆H/δT)p = ∆ (δH/δT)p = ∆Сp
(δ∆U/δT)V = ∆ (δU/δT)V = ∆Сv, Эти уравнения носят имя Кирхгофа.
∆Сp, ∆Сv – изменение теплоемкостей при постоянном давлении и объеме. Если взять реакцию: aA + bB = dD + сС, то изменение теплоемкости вещества в ходе реакции можно рассчитать по уравнению:
∆Сp =∑ν(пр.) ∆Сp (пр.) - ∑ν(исх.) ∆Сp (исх.)
Если реакция протекает экзотермично и ∆Сp > 0, то по уравнению Кирхгофа температурный коэффициент тоже больше нуля и реакция становится еще более эндотермичной (тепловой эффект более положительным) (δ∆H/δT)p > 0. для вычисления теплового эффекта при температуре Т2 если известен тепловой эффект при Т1 можно использовать интегрированное уравнение Кирхгофа.
4. Второе начало термодинамики. Энтропия.
Второе начало термодинамики дает возможность определить, какой из процессов будет протекать самопроизвольно, какое количество работы может быть при этом получено, каков предел самопроизвольного течения процесса. Далее, второе начало термодинамики дает возможность определить, какими должны быть условия, чтобы нужный процесс протекал в необходимом направлении и в требуемой степени, что особенно важно для решения различных задач прикладного характера. Подобно первому, второе начало термодинамики выведено непосредственно из опыта. В то же время второе начало термодинамики имеет ограниченную область применения: оно применимо лишь к макроскопическим системам. Ниже приведены некоторые формулировки второго начала термодинамики:
Теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому (постулат Клаузиуса).
Невозможен процесс, единственным результатом которого является превращение теплоты в работу.
Невозможно построить машину, все действия которой сводились бы к производству работы за счет охлаждения теплового источника (вечный двигатель второго рода).
Любая форма энергии может полностью перейти в теплоту, но теплота преобразуется в другие формы энергии лишь частично.
Т.о., можно условно принять, что внутренняя энергии системы состоит из двух составляющих: "свободной" X и "связанной" Y энергий, причем "свободная" энергия может быть переведена в работу, а "связанная" энергия может перейти только в теплоту.
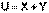 (I.44)
(I.44)
Величина связанной энергии тем больше, чем меньше разность температур, и при T = const тепловая машина не может производить работу. Мерой связанной энергии является новая термодинамическая функция состояния, называемая энтропией.
В изолированных системах самопроизвольно могут протекать только процессы, сопровождающиеся увеличением энтропии.
Энтропия изолированной системы не может самопроизвольно убывать.
Оба этих вывода также являются формулировками второго начала термодинамики
Статистическая интерпретация энтропии
Классическая термодинамика рассматривает происходящие процессы безотносительно к внутреннему строению системы; поэтому в рамках классической термодинамики показать физический смысл энтропии невозможно. Для решения этой проблемы Больцманом в теорию теплоты были введены статистические представления. Каждому состоянию системы приписывается термодинамическая вероятность (определяемая как число микросостояний, составляющих данное макросостояние системы), тем большая, чем более неупорядоченным или неопределенным является это состояние. Т.о., энтропия есть функция состояния, описывающая степень неупорядоченности системы. Количественная связь между энтропией S и термодинамической вероятностью W выражается формулой Больцмана:
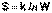 (I.58)
(I.58)
С точки зрения статистической термодинамики второе начало термодинамики можно сформулировать следующим образом:
Система стремится самопроизвольно перейти в состояние с максимальной термодинамической вероятностью.
Статистическое толкование второго начала термодинамики придает энтропии конкретный физический смысл меры термодинамической вероятности состояния системы. Второе начало термодинамики разделяет все процессы на возможные и невозможные, оно позволяет определить направление процесса, и установить когда наступит равновесие системы.
Все процессы делят:
1. Положительные, самопроизвольные, естественные – протекают без внешнего вмешательства, протекают за счет уменьшения внутренней энергии. (Могут быть эндо- и экзотермическими) Примеры – расширение газа в пустоту, работа гальванического элемента с поглощением теплоты из окружающей среды и отдачей работы….
2. Отрицательные, не самопроизвольные, не естественные процессы – требуют внешнего воздействия изменение внутренней энергии любое, не могут протекать в изолированных системах. (Могут быть эндо- и экзотермическими) Примеры переход тепла от холодного тела к горячему.
3. Обратимый процесс – и систему и среду, в которой находится система можно вернуть в исходное состояние.
4. Необратимый процесс – и систему и среду или что-то одно нельзя вернуть в исходное состояние.
Обратимость – необратимость зависит от способа проведения процесса. Работа обратимого процесса максимальна, хотя процесс идет бесконечно медленно.
Второе начало:
Ни какая совокупность процессов не может свестись только к передачи тепла от холодного тела к горячему, обратное возможно.
Нельзя всю имеющуюся теплоту превратить в работу – обратное возможно.
Вечный двигатель второго рода не возможен.
Так второе начало разделяет процессы на те, которые возможны и нет.
Для обратимых процессов второе начало выступает как закон существования энтропии:
dS = δQ/T
Для необратимых процессов как закон существования и возрастания энтропии:
dS > δQ/T
Объединение первого и второго начал:
T dS ≥ dU + δW
S – Энтропия, - это функция состояния системы, которая характеризует направление процесса для самопроизвольных процессов ∆S > 0 и момент равновесия системы ∆S = 0.
Она возрастает с увеличением числа возможных состояний и положений, которые могут принимать элементы, слагающие систему, поэтому ее называют степенью беспорядка. Она также растет с Т.
|
|
|


