Изотерма реакции. Ее анализ

Рассмотрим произвольную реакцию:

аА + вВ = сС + мМ (7.4)

Любая реакция идет до тех пор, пока не установится состояние равновесия, которому будет отвечать ∆ μ_i = 0. Это равновесие не является устойчивым, любое изменение внешних термодинамических параметров влечет за собою изменение положения равновесия. Поэтому химические реакции можно рассматривать как термодинамически равновесные. В ходе реакции количество молей исходных веществ уменьшается (берутся с минусом), количество продуктов увеличивается, поэтому в изобарно изотермических условиях:

dG _{T, P} = - μ_adn_A - μ_bdn_B + μ_cdn_C + μ_mdn_M (7.5)

Введем для упрощения Х – химическую переменную – количества молей прореагировавшего вещества к его стехиометрическому коэффициенту (изменяется от 0 до 1). dX_a = dn_A/a, dn_A = dX_a*a. (7.5)

Проведем замену и разделим на dX.

d∆G _{T, P} = (dG /dX)_{T, P} = ∑ μ_idni (7.6)

Для того чтобы вывести уравнение изотермы, вспомним характеристические функции

V = (δG/δP)_T, для одного моля

dμ = Vdp или dμ = (RT/P)dp, (7.7)

dμ_i = RTdlnf, (7.8)

f – фугитивность то, что мы используем для уравнений выведенных для идеальных газов чтобы иметь возможность применить их для реальных газов. f = γp. γ – коэффициент активности суммарно учитывает все отличая реального газа от идеального.

После интегрирования:

μ = μ⁰ + RTlnf (7.9)

μ⁰ – стандартное значение химического потенциала. При стандартный условиях P = 1 атм, Т = 298^ОК.

После подстановки (7.9) для каждого компонента в (7.6):

d∆G _{T, P} = RTlnП_f/ - RTlnK_f (7.9)

П_f/ = (f^/_cf^/_d)/(f^/_af^/_b) (7.10)

K_f = 1/RT(aμ^/_A + bμ^/_B - cμ^/_C - dμ^/_D)

Уравнение (7.9) называется уравнением изотермы реакции оно подходит для любых систем, только если реакция проходит в среде идеальных газов то вместо фугитивности используется давление, если в жидких или твердых идеальных растворах по концентрации, если в реальных растворах то активности.

Проанализируем (7.9).

Если П_f/ > K_f то ∆G > 0. Реакция идет в обратном направлении.

Если П_f/ < K_f то ∆G < 0. Реакция идет в прямом направлении.

Если П_f/ = K_f то ∆G = 0. Реакция не идет, состояние равновесия

Количественной характеристикой химического равновесия является константа равновесия, которая может быть выражена через равновесные концентрации С, парциальные давления P или мольные доли X реагирующих веществ. Для некоторой реакции

соответствующие константы равновесия выражаются следующим образом:

(I.78) (I.79)

(I.80)

Константа равновесия есть характерная величина для каждой обратимой химической реакции; величина константы равновесия зависит только от природы реагирующих веществ и температуры. Выражение для константы равновесия для элементарной обратимой реакции может быть выведено из кинетических представлений.

Рассмотрим процесс установления равновесия в системе, в которой в начальный момент времени присутствуют только исходные вещества А и В. Скорость прямой реакции V₁ в этот момент максимальна, а скорость обратной V₂ равна нулю:

(I.81)

(I.82)

По мере уменьшения концентрации исходных веществ растет концентрация продуктов реакции; соответственно, скорость прямой реакции уменьшается, скорость обратной реакции увеличивается. Очевидно, что через некоторое время скорости прямой и обратной реакции сравняются, после чего концентрации реагирующих веществ перестанут изменяться, т.е. установится химическое равновесие.

Приняв, что V₁ = V₂, можно записать:

(I.83)

(I.84)

Т.о., константа равновесия есть отношение констант скорости прямой и обратной реакции. Отсюда вытекает физический смысл константы равновесия: она показывает, во сколько раз скорость прямой реакции больше скорости обратной при данной температуре и концентрациях всех реагирующих веществ, равных 1 моль/л.

Теперь рассмотрим (с некоторыми упрощениями) более строгий термодинамический вывод выражения для константы равновесия. Для этого необходимо ввести понятие химический потенциал. Очевидно, что величина свободной энергии системы будет зависеть как от внешних условий (T, P или V), так и от природы и количества веществ, составляющих систему. В случае, если состав системы изменяется во времени (т.е. в системе протекает химическая реакция), необходимо учесть влияние изменения состава на величину свободной энергии системы. Введем в некоторую систему бесконечно малое количество dn_i молей i-го компонента; это вызовет бесконечно малое изменение термодинамического потенциала системы. Отношение бесконечно малого изменения величины свободной энергии системы к бесконечно малому количеству компонента, внесенному в систему, есть химический потенциал μ_i данного компонента в системе:

(I.85)

(I.86)

Химический потенциал компонента связан с его парциальным давлением или концентрацией следующими соотношениями:

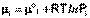(I.87)

(I.88)

Здесь μ°_i – стандартный химический потенциал компонента (P_i = 1 атм., С_i = 1 моль/л.). Очевидно, что изменение свободной энергии системы можно связать с изменением состава системы следующим образом:

(I.89)

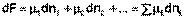(I.90)

Поскольку условием равновесия является минимум свободной энергии системы (dG = 0, dF = 0), можно записать:

(I.91)

В закрытой системе изменение числа молей одного компонента сопровождается эквивалентным изменением числа молей остальных компонентов; т.е., для приведенной выше химической реакции имеет место соотношение:

(I.92)

Отсюда можно получить следующее условие химического равновесия в закрытой системе:

(I.93)

В общем виде условие химического равновесия можно записать следующим образом:

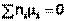(I.94)

Выражение (I.94) носит название уравнения Гиббса – Дюгема. Подставив в него зависимость химического потенциала от концентрации, получаем:

(I.95)

Поскольку Σn_iμ_i = ΔF, а Σn_iμ°_i = ΔF°, получаем:

(I.96)

Для изобарно-изотермического процесса аналогичным образом можно получить:

(I.97)

Полученные нами выражения I.96 – I.97 есть изотерма химической реакции. Если система находится в состоянии химического равновесия, то изменение термодинамического потенциала равно нулю; получаем:

(I.98)

(I.99)

Здесь с_i и р_i – равновесные концентрации и парциальные давления исходных веществ и продуктов реакции (в отличие от неравновесных С_i и Р_i в уравнениях I.96 – I.97).

Поскольку для каждой химической реакции стандартное изменение термодинамического потенциала ΔF° и ΔG° есть строго определенная величина, то произведение равновесных парциальных давлений (концентраций), возведенных в степень, равную стехиометрическому коэффициенту при данном веществе в уравнении химической реакции (стехиометрические коэффициенты при исходных веществах принято считать отрицательными) есть некоторая константа, называемая константой равновесия. Уравнения (I.98, I.99) показывают связь константы равновесия со стандартным изменением свободной энергии в ходе реакции. Уравнение изотермы химической реакции связывает величины реальных концентраций (давлений) реагентов в системе, стандартного изменения термодинамического потенциала в ходе реакции и изменения термодинамического потенциала при переходе из данного состояния системы в равновесное. Знак ΔG (ΔF) определяет возможность самопроизвольного протекания процесса в системе. При этом ΔG° (ΔF°) равно изменению свободной энергии системы при переходе из стандартного состояния (P_i = 1 атм., С_i = 1 моль/л) в равновесное. Уравнение изотермы химической реакции позволяет рассчитать величину ΔG (ΔF) при переходе из любого состояния системы в равновесное, т.е. ответить на вопрос, будет ли химическая реакция протекать самопроизвольно при данных концентрациях С_i (давлениях Р_i) реагентов:

(I.100)

(I.101)

Если изменение термодинамического потенциала меньше нуля, процесс в данных условиях будет протекать самопроизвольно.

 

9. Изобара реакции, ее анализ.

Химическая термодинамика позволяет определить константу равновесия при одной температуре, если она известна при другой. (Константа равновесия позволяет нам оценить оптимальные значения концентраций реагентов, условия реакции). Если реакция протекает в газовой среде, то это становится возможным благодаря уравнению изобары, если в жидком растворе уравнению изохоры.

Выведем уравнение изобары. Возьмем производную уравнения изотермы по температуре при постоянном давлении.

d∆G _{T, P} = RTlnП_f/ - RTlnK_f (9.1)

(δ∆G/δT)_P = RlnП_f/ - RlnK_f – RT(δlnK_f/δT)_P (9.2)

С другой стороны:

∆G = ∆H + T (δ∆G/δT)_P (9.3)

∆G = ∆H + RTlnП_f/ - RТlnK_f – RT²(δlnK_f/δT)_P

или

∆G = ∆H + ∆G +– RT²(δlnK_f/δT)_P

или

∆H/RT² = (δlnK_f/δT)_P

Если ∆H больше нуля, то температурный коэффициент (δlnK_f/δT)_P тоже больше нуля, реакция эндотермическая и при подъеме температуры реакция смещается в сторону продуктов. Если тепловой эффект ∆H меньше нуля, то температурный коэффициент тоже меньше нуля и экзотермическая реакция при подъеме Т смещается в сторону исходных веществ.

При постоянном объеме, используя ∆A = ∆U + T (δ∆A/δT)_V, (6.5), можно получить уравнение изохоры:

∆U/RT² = (δlnK_f/δT)_V

Анализ аналогичен.

 

10. Понятия и определения, относящиеся к фазовым равновесиям.

 

Система, состоящая из одной фазы, называется гомогенной, из двух и более гетерогенной.

Фаза – совокупность гомогенных частей системы, одинаковых по составу и другим термодинамическим свойствам, ограниченная от других частей поверхностью раздела.

Компонент – вещество, которое может быть выделено из системы, и существовать, не зависимо от нее.

Число независимых компонентов – наименьшее число компонентов, через концентрации которых можно охарактеризовать состав всей системы в целом.

Понятно, что число независимых компонентов зависит от того, что мы знаем о системе, чем больше наших знаний, тем меньше компонентов.

H_2(г) + I_2(г) = 2HI_(г)

В этой системе один независимый компонент, во первых исходные вещества и продукты связаны константой равновесия, во вторых количество водорода по реакции равно количеству йода, поэтому задавая только количество йодоводорода мы автоматически задаем количества и концентрации водорода и йода. Если бы вещества были в разы фазах, то число независимых компонентов было бы больше.
Вещество при изменении давления и температуры может переходить из одного агрегатного состояния в другое. Эти переходы, совершающиеся при постоянной температуре, называют фазовыми переходами первого рода. Количество теплоты, которое вещество получает из окружающей среды либо отдает окружающей среде при фазовом переходе, есть скрытая теплота фазового перехода λ_фп. Если рассматривается гетерогенная система, в которой нет химических взаимодействий, а возможны лишь фазовые переходы, то при постоянстве температуры и давления в системе существует т.н. фазовое равновесие. Фазовое равновесие характеризуется некоторым числом фаз, компонентов и числом степеней термодинамической свободы системы.

Компонент – химически однородная составная часть системы, которая может быть выделена из системы и существовать вне её. Число независимых компонентов системы равно числу компонентов минус число возможных химических реакций между ними.

Число степеней свободы – число параметров состояния системы, которые могут быть одновременно произвольно изменены в некоторых пределах без изменения числа и природы фаз в системе.

Число степеней свободы гетерогенной термодинамической системы, находящейся в состоянии фазового равновесия, определяется правилом фаз, сформулированным Дж. Гиббсом:

Число степеней свободы равновесной термодинамической системы С равно числу независимых компонентов системы К минус число фаз Ф плюс число внешних факторов, влияющих на равновесие.

Для системы, на которую из внешних факторов влияют только температура и давление, можно записать:

С = К – Ф + 2 (I.108)

Системы принято классифицировать по числу компонентов (одно-, двухкомпонентные и т.д.), по числу фаз (одно-, двухфазные и т.д.) и числу степеней свободы (инвариантные, моно-, дивариантные и т.д.). Для систем с фазовыми переходами обычно рассматривают графическую зависимость состояния системы от внешних условий – т.н. диаграммы состояния.

Анализ диаграмм состояния позволяет определить число фаз в системе, границы их существования, характер взаимодействия компонентов. В основе анализа диаграмм состояния лежат два принципа: принцип непрерывности и принцип соответствия. Согласно принципу непрерывности, при непрерывном изменении параметров состояния все свойства отдельных фаз изменяются также непрерывно; свойства системы в целом изменяются непрерывно до тех пор, пока не изменится число или природа фаз в системе, что приводит к скачкообразному изменению свойств системы. Согласно принципу соответствия, на диаграмме состояния системы каждой фазе соответствует часть плоскости – поле фазы. Линии пересечения плоскостей отвечают равновесию между двумя фазами. Всякая точка на диаграмме состояния (т. н. фигуративная точка) отвечает некоторому состоянию системы с определенными значениями параметров состояния.

11. Уравнения Клаузиуса-Клапейрона и его анализ.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: