Растворы. Идеальные и неидеальные растворы, отклонения от идеальности.

 

Растворы бывают твердыми жидкими и газообразными.

Истинный раствор – это гомогенная, термодинамически устойчивая система переменного состава, состоящая из двух и более компонентов, между которыми есть сильные взаимодействия. (Кто не выучит тому кол).

Раствор это однофазная система, в которой нет поверхности раздела. Его свойства непрерывно меняются с составом, при образовании раствора происходило уменьшение изобарно-изотермического потенциала и увеличение энтропии, поэтому такая система в неизменных условиях устойчива.

Частицы растворителя и растворенного вещества взаимодействуют между собой. Взаимодействия эти есть всегда. Хотя характер может быть различен. Растворитель может сольватировать и это приведет к отрицательным отклонениям. Здесь взаимодействие между растворителем и растворенным веществом энергетически предпочтительнее, нежели взаимодействия индивидуальных веществ.

Взаимодействия могут быть и такого рода, что растворенное вещество и растворитель меняя способ упаковки молекул в растворе, будут стремиться уйти друг от друга на расстоянии и это приведет к положительным отклонениям. Такое происходит, когда взаимодействия между индивидуальными веществами предпочтительнее, чем веществом и растворителем.

Раулем для идеальных растворов был выведен закон.

Р_i = хР^o_i (13.1)

Давление пара растворителя над растворам Р_i прямо пропорционально мольной доли растворителя. Р^o_i - давление растворителя над чистым растворителем.

Для реальных растворов давление пара растворителя над раствором либо больше (положительные отклонения), либо меньше (отрицательные отклонения).

Величина f_i=a_i=P_i/P⁰_i –называется активностью или фугитивностью i-го компонента в растворе. В этом отношении суммарно учтены все отклонения от идеальности и, используя его вместо концентрации, мы можем пользоваться всеми уравнениями термодинамики для реальных растворов. С_i = γ _ia_i γ _I – коэффициент активности.

Образование любого реального раствора сопровождается тепловыми эффектами. Если положим, мы растворяем, к примеру, NaCl то это будет теплота разрушения кристаллической решетки (эндотермический процесс) и теплота сольватации (экзотермический процесс). Суммарный тепловой эффект будет равен нулю но, понятно что с ростом Т растворимость будет увеличиваться, а сольваты разрушаться.

При смешении исходных веществ сумма объемов исходных веществ не будет равна объему полученного раствора, V_в-во + V_р-тель ≠ V_{раствор}.

Для отрицательных отклонений:

Тепловой эффект отрицателен ∆Н<0.

При более сильном взаимодействии веществ изменение объема отрицательно V_в-во + V_р-тель < V_{раствор}. ∆V<0 это эквивалентно работе над системой.

При отрицательных отклонениях γ <1 a=P_i/P⁰_i<1.

Для положительных отклонений:

Тепловой эффект системы положителен ∆Н>0. Такое произойдет, если мы будем смешивать воду и нафталин. Нафталин очень мало растворим в воде, для растворение потребуется затратить энергию извне.

∆V>0, γ >1, a=P_i/P⁰_i>1.

Идеальный раствор – тот, который подчиняется закону Рауля, для которого ∆Н=0, ∆V=0, γ =1, a=P_i/P⁰_i=1, С_i = a_i.

 

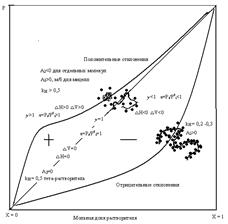
Рис. 2. Зависимость давления пара растворителя над раствором от его мольной доли. Второй компонент твердое вещество.

 

15. Диаграммы Р = f(состав), Т = f(состав). Азеотропа. Правило рычага.

Если смешиваются два химических соединения то, нельзя сходу сказать, как они поведут себя вместе. Они могут образовать истинный раствор, а могут расслоиться подобно маслу и воде при комнатной температуре. В последнем случае у нас образуется сразу два раствора находящиеся в равновесии друг с другом. Раствор воды в масле и раствор масла в воде.

Нам необходимо охарактеризовать полученные растворы, понять их свойства, чтобы в последствии использовать знания на практике.

Величина, которую всегда стремятся получить это активность. Она позволяет рассчитать химический потенциал смешения. А из последнего можно получить все термодинамические параметры.

a=p_i/p⁰_i

∆s _i = -RT ln a_i, ∆s _i = -R ln a_i, ∆μ _i =∆h_i - T∆s _i

∆s _i, ∆ μ _i, ∆h_i – парциальные мольные энтропия, энергия Гиббса, энтальпия.

Так как активность зависит от давления пара растворителя над раствором при определенной температуре, то строят зависимости: P_общ, P_i = f(x,x^/), P_общ = f(x,x^/), T_кип = f(x,x^/), x^/ = f(x),

x – доля вещества в жидкой фазе, x^/ - доля вещества в паровой фазе.

Рассмотрим их по порядку.

 

P_общ, P_i = f(x,x^/).

Кривая АВ на рис 5.1 зависимость общего давления от состава. АD – кривая зависимости парциального давления первого компонента от состава. CB – кривая зависимости второго компонента от состава. Прямые линии соответствуют давлению в идеальном растворе. Доля первого компонента в паровой фазе очевидно равна: X₁^/ = P₁ / P. P₁ + P₂ = P.

рис 5.1. P_общ, P_i = f(x,x^/). рис. 5.2. P_общ = f(x,x^/).

 

P_общ = f(x,x^/).

На рис. 5.2 кривая ABC – характеризует при постоянной Т зависимость общего давления пара от состава жидкой фазы. Кривая ADC - зависимость общего давления от состава паровой фазы. В общем случае составы фаз различны. В точке В жидкость имеет состав X_{M ЖИДК}. Раствор находится в равновесии с паровой фазой D. Паровая фаза имеет состав X_{M ПАРОВ}.

 

T_кип = f(x,x^/).

 

На рис. 5.3 кривая AМ*C - зависимость температуры кипения от состава пара. АМB – кривая зависимости температуры кипения от состава жидкости. Если мы возьмем жидкость состава X_{M ЖИДК} и доведем ее до кипения Тм в точке М, то она будет находиться в равновесии с паровой фазой – точка М* (паровая фаза более богата вторым компонентом). Если мы сконденсируем эту фазу и снова доведем до кипения, у паровой фазы будет новый состав еще более богатый вторым компонентом. На этом основана перегонка.

Правило рычага.

В точке D масса пара так будет относиться к массе жидкости как MD/DM*.

MD/DM* = m_пара/m_жидк. Если учесть что m_пара + m_жидк = m _общ, то можно определить массовые доли паровой и жидкой фаз.

 

 

x^/ = f(x).

На рис. 5.4. показана зависимость состава пара от состава жидкости.

 

рис. 5.3. T_кип = f(x,x^/). рис. 5.4. x^/ = f(x).

 

Азеотропа – точка соответствующая экстремуму (рис. 5.5.) на кривых P_общ = f(x,x^/), T_кип = f(x,x^/). В ней составы жидкости и пара одинаковы. Если система имеет азеотропу то можно выделить из раствора одно чистое вещество и азеотропную смесь. Максимум на кривой испарения соответствует минимуму кривой кипения и наоборот.

рис. 5.5. Азеотропы.

 

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: